| Figure 1: Wage Frontier for a Fixed Capital Example |
This post presents a perturbation of parameters in a 'one good' model of fixed capital. The coefficients of production differ from those in this reswitching example. But the model has the same structure.
Consider a one-commodity economy in which labor and widgets are used to produce new widgets, the only consumption good. (The use of the term 'widget' to designate the single produced commodity emphasizes how unrealistic this model is.) New widgets last several years when used in producing widgets. In this particular answer to Steedman's homework assignment, they last three years. And their efficiency can vary throughout their technical lifetime. Accordingly, Tables 1 and 2 specify the coefficients of production for three processes.
| Input | Process | ||
| (I) | (II) | (III) | |
| Labor | a0,1 | a0,2 | a0,3 |
| New Widgets | 1 | 0 | 0 |
| One-Year Old Widgets | 0 | 1 | 0 |
| Two-Year Old Widgets | 0 | 0 | 1 |
| Output | Process | ||
| (I) | (II) | (III) | |
| New Widgets | b1,1 | b1,2 | b1,3 |
| One-Year Old Widgets | 1 | 0 | 0 |
| Two-Year Old Widgets | 0 | 1 | 0 |
Firms are not required to operate all three processes. They can truncate the use of widgets after one or two years. The choice of technique in this model is equivalent to the choice of the economic life of a widget. In the Alpha technique, the widget is operated for one year; in the Beta technique, it is operated for two years; and in the Gamma technique, it is operated for the full three years.
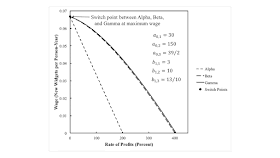
The wage frontier is the outer envelope of all wage curves. In models of circulating and fixed capital without superimposed joint production, the cost-minimizing technique, at a given rate of profits, is the technique which contributes its wage curve to the frontier at that rate. The Gamma technique is cost-minimizing in Figure 1 for all feasible rates of profits. Wage curves, when on the frontier, are declining functions of the rate of profits. At a switch point, more than one technique is cost-minimizing. At a rate of profits of zero in Figure 1, the Alpha, Beta, and Gamma techniques are all cost-minimizing.
The single switch point in Figure 1 is a fluke case several times over. It is the intersection of three wage curves, not two. And the switch point is on the wage axis, occurring for a rate of profits of zero. These properties are destroyed by any variation in certain coefficients of production. Figure 2 illustrates variations in b1,2 and b1,3. (The numbering of regions are consistent with this post.) The location in parameter space for fluke switch points, which I call patterns of switch points, is shown. Consider parameters in Region 4, and suppose b1,2 is increased. Eventually, a fluke case will arise in which the switch point between the Alpha and Beta technique is on the wage axis. When b1,2 > 10, this switch point will no longer occur for a non-negative rate of profits. It will only be cost-minimizing to run widgets for two or three years, depending on distribution. On the other hand, consider an increase in b1,3. The switch points between Alpha and Beta and between Beta and Gamma will eventually coincide, in a single switch point at a positive rate of profits. With any further increase in this parameter, it is no longer cost minimizing to run widgets for two years, whatever the distribution of income.
| Figure 2: Selected Regions in Parameter Space |
Tables 3 and 4 summarize the choice of technique in each region in Figure 2. Negative real Wicksell effects occur at all switch points in the four regions in Figure 2. According to traditional Austrian and marginalist dogma, one might expect an increase in capital intensity to go along with a longer economic life of a widget. This idea is proven to be untrue in Regions 1, 4, and 5. Is the jump over an economic life of two years in Region 1 surprising? Adjacent techniques on the wage frontier need not be near in a parameter space formed by coefficients of production. Continuity in the wage frontier does not imply continuous variation in coefficients of production. In this case, the three-technique pattern of switch points illustrates how managers of firms come to eliminate the choice of the Beta technique.
| 1 | 0 ≤ r ≤ r1 | Widgets operated for one year |
| r1 ≤ r ≤ rγ | Widgets operated for three years | |
| 3 | 0 ≤ r ≤ rγ | Widgets operated for three years |
| 4 | 0 ≤ r ≤ r1 | Widgets operated for one year |
| r1 ≤ r ≤ r2 | Widgets operated for two years | |
| r2 ≤ r ≤ rγ | Widgets operated for three years | |
| 5 | 0 ≤ r ≤ r1 | Widgets operated for two years |
| r1 ≤ r ≤ rγ | Widgets operated for three years |
| 1 | A larger rate of profits is associated with a longer economic life of a widget. |
| 3 | No switch points. |
| 4 | A larger rate of profits is associated with a longer economic life of a widget. |
| 5 | A larger rate of profits is associated with a longer economic life of a widget. |
This structure in a two-dimensional parameter space is generic, in some sense. Three partitions of patterns over the wage axis intersect in the start of a ray that is a partition for a three-technique pattern. A corresponding structure exists for patterns over the axis for the rate of profits.

I see this post in connection with Fluke Switch Points At Both The Maximum Wage And The Maximum Rate Of Profits' post. It would be interesting to see if at the former one can see a Three-Technique patter over both axis and if at the later one can see not Two-Technique patters but also Three-Technique patterns over both axis without a technique being dominated for all rates as it seems in that post.
ReplyDeleteIt seems like there is a taxonomy of switch points. In the case of one commodity with fixed capital if there is a triple switch then there is an impossibility of other switches. If the switch for the one commodity model is double then there is a possibility for another double switch with alternation. It looks like the one commodity model being a prototype for exploring the more complex two commodity with fixed capital case. At the two commodity case we see the same for the quadruple switch as what we see for the triple one on one commodity model being it the exclusion of other switches. For the triple switch on the two commodity model we can see a situation where there is no switch in between two triple alternating switches at both axis. With alternating switches I means for example a switch with alpha and beta and the other with beta and gamma or in the two commodity case at one axis alpha beta and gamma and at the other beta gamma and delta. I also would find interesting how the openness of the unique rate of profits or wage rate could enrich the taxonomy opening space for quadruple switch points at both axis or in-between switch points for the triple switching case.
ReplyDeleteAnother stream of thought would be reducing at both the one commodity and the two commodity model from a two year widget or machine to just a one year old ones. And to see there the taxonomy for both models. At the case of a corn-tractor model an analogy of this post would be obtained. At the case of a corn-widget model the analogous of this post would be a A Two-Technique pattern over the wage axis. The motto would be the possibility of reswitching at the modified corn-tractor model without 2 year old tractors but the impossibility of reswitching at the modified corn-widget model without 2 year old widget. Just to finish I would like to comment how a non-unique wage rate at the corn-widget model could bring reswitching to the 1 year old one.
ReplyDeleteJust to be concrete. A post could be entitled Fluke Switch Points At Both The Maximum Wage And The Maximum Rate Of Profits On A One-Commodity Minimum Fixed Capital Model. This one-commodity fixed capital model would be a model with widgets with a maximal life of 1 year so that the technique set is reduced to Alpha and Beta, no Gamma exists at the minimum fixed capital model. Then without more complications one could obtain a pattern for a switch and could work on the parameters to move the switchpoint up to the wage axis and down to the rate of profits axis. One could study when the switchpoint is at negative rates of profits or at negative wage rate and in other words outside of the first quadrant. If we introduce one last complication as different wages for alpha and beta then we can work on the newborn switchpoint to move it with a variation of the parameters to have one at the wage axis and the other at the profit rate one.
ReplyDeletePS: With the corn-tractor minimum fixed capital model instead of having different wages for alpha, beta and gamma one can have differential rates of profits and play with the parameters to obtain a fluke with a three-technique pattern at the wage axis and another three-technique pattern at the rate of profits axis.
A justification for the institutional framework one can think about 3 different case for the differential wages. First a Trumpian Economy where black men are segregated from white men and each group works on a sector and there is a race gap in salaries. Another case would be an Opus Dei Economy where women and men are segregated and there is a gender gap in wages. Finally we can think about a Heteropatriarchal Economy where single men work on one sector and married men work on the other with higher salaries for the married ones.
ReplyDelete