In the previous part, I presented a specification of the technology in a numeric example created by Lynn Mainwaring. Which technique specified by this technology is cost minimizing at equilibrium prices? In this context, equilibria have the following properties:
- The iron-producing process, at least one steel-producing process, and at least one corn-producing process are operated.
- The costs of inputs for each process in operation does not exceed revenues.
- No process can be used to obtain pure economic profits.
Suppose, for example, that the Alpha technique is cost minimizing. Given these properties, then the following equations must be satisfied:
(1/5) p2 (1 + r) + (1/20) w = p1
[(1/5) p1 + (1/10)](1 + r) + (1/5) w = p2
[(1/10) p1 + (1/2) p2](1 + r) + (9/20) w = 1
where
- w is the wage (in units of bushels per person-year)
- r is the rate of profits
- p1 is the price of iron (in units of bushels per ton iron)
- p2 is the price of steel (in units of bushels per ton steel)
The above equations specify that, for each process in the Alpha technique, costs of inputs in the process equal revenues. The costs do not exceed revenues. Furthermore, no process, at least in the Alpha technique, can be operated to obtain pure economic process.
Suppose, for mathematical convenience, the rate of profits is externally specified. Then the above is a system of three linear equations in three variables. It can be solved, and the solution is:
w = 2 [500 - 45(1 + r)^2 - (1 + r)^3]/[450 + 105(1 + r) - 9 (1 + r)^2]
p1 = (1/2) [100 + 80(1 + r) + 13(1 + r)^2]/[450 + 105(1 + r) - 9(1 + r)^2]
p2 = (1/2)[400 + 110(1 + r) + (1 + r)^2]/[450 + 105(1 + r) - 9(1 + r)^2]
A system of equations is associated each of the remaining three techniques defined by the technology. The statement of those systems and their solutions is relegated to an appendix. The cost minimizing technique at any given rate of profits can be found from these solutions. In particular, Figure 3-1 shows a graph of the wage as a function of the rate of profits for each technique. The cost minimizing technique at a given rate of profits is the technique for which the wage is greatest. The figure shows the frontier defined by this criteria as a heavy black line. The Delta technique is cost minimizing at low rates of profits. The Beta technique is cost minimizing at intermediate rates of profits, and the Alpha technique is cost minimizing at intermediate rates of profits.
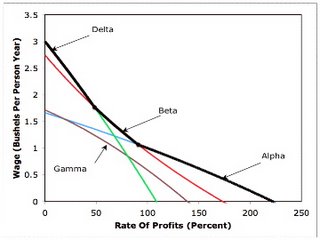 |
|---|
| Figure 3-1: The Wage-Rate Of Profits Frontier |
But what does all of this have to do with the theory of international trade? This question will be answered in the next part.
Appendix 3.A: Price Equations For Three Techniques
Appendix 3.A.1: The Beta Technique
The price equations for the Beta technique are:
(1/5) p2 (1 + r) + (1/20) w = p1
[(1/5) p1 + (1/10)](1 + r) + (1/5) w = p2
(43/25) p1 (1 + r) + (19/100) w = 1
The solution to the Beta price equations is:
w = (2)[1,250 - 50(1 + r)^2 - 43(1 + r)^3]/[153(1 + r)^2 + 215(1 + r) + 475]
p1 = (1/2)[19(1 + r)^2 + 200(1 + r) + 250]/[153(1 + r)^2 + 215(1 + r) + 475]
p2 = (1/2)[43(1 + r)^2 + 145(1 + r) + 1,000]/[153(1 + r)^2 + 215(1 + r) + 475]
Appendix 3.A.2: The Gamma Technique
(1/5) p2 (1 + r) + (1/20) w = p1
(8/25)(1 + r) + (3/50) w = p2
[(1/10) p1 + (1/2) p2](1 + r) + (9/20) w = 1
The solution to the Gamma price equations is:
w = 8[625 - 100(1 + r)^2 - 4(1 + r)^3]/[6(1 + r)^2 + 175(1 + r) + 2,250]
p1 = 2[52(1 + r)^2 + 30(1 + r) + 125]/[6(1 + r)^2 + 175(1 + r) + 2,250]
p2 = 4 [2(1 + r)^2 + 180(1 + r) + 75]/[6(1 + r)^2 + 175(1 + r) + 2,250]
Appendix 3.A.3: The Delta Technique
The price equations for the Delta technique are:
(1/5) p2 (1 + r) + (1/20) w = p1
(8/25)(1 + r) + (3/50) w = p2
(43/25) p1 (1 + r) + (19/100) w = 1
The solution to the Delta price equations is:
w = 4 [3,125 - 344(1 + r)^3]/[258(1 + r)^2 + 1,075(1 + r) + 2,375]
p1 = [152(1 + r)^2 + 150(1 + r) + 625]/[258(1 + r)^2 + 1,075(1 + r) + 2,375]
p2 = [344(1 + r)^2 + 760(1 + r) + 750]/[258(1 + r)^2 + 1,075(1 + r) + 2,375]



