"Curiously, though economists like to intimidate other social scientists with the mathematical rigor of their discipline, most economists do not have this level of mathematical education...
...One example of this is the way economists have reacted to 'chaos theory'... Most economists think that chaos theory has had little or no impact - which is generally true in economics, but not at all true in most other sciences. This is partially because, to understand chaos theory, you have to understand an area of mathematics known as 'ordinary differential equations.' Yet this topic is taught in very few courses on mathematical economics - and where it is taught, it is not covered in sufficient depth. Students may learn some of the basic techniques for handling what are known as 'second-order linear differential equations,' but chaos and complexity begin to manifest themselves only in 'third order nonlinear differential equations.' Steve Keen (2011). Debunking Economics: The Naked Emperor Dethroned?, Revised and expanded ed. Zed Books, p. 31
The above quotes are also in the first edition. Before commenting on this passage, I want to re-iterate my previously expressed belief that some economists, including some mainstream economists, understand differential and difference equations.
I misremembered this comment as being overstated for polemical purposes. But, in context, I think it is clear to those who know the mathematics.
I took an introductory course in differential equations decades ago. Our textbook was by Boyce and DiPrima. As I recall, we were taught fairly cookbook techniques to solve linear differential equations. These could be first order or second order and homogeneous or non-homogeneous. They could also be systems of linear differential equation. I recall some statement of an existence theorem for Initial Value Problems (IVPs), although I think I saw a more thorough proof of some such theorem in an introductory1 real analysis course. We might have also seen some results about the stability of limit points for dynamical systems. Keen is not claiming that economists do not learn this stuff; this kind of course is only a foundation for what he is talking about.
I also took a later applied mathematics course, building on this work. In this course, we were taught how to linearize differential equations. We definitely were taught stability conditions here. If I recall correctly, the most straightforward approach looked only at sufficient, not necessary conditions. We also learned perturbation theory, which can be used to develop higher order approximations to nonlinear equations around the solutions to the linearized equations. One conclusion that I recall is that the period of an unforced pendulum depends on the initial angle, despite what is taught in introductory physics classes2. I do not recall much about boundary layer separations, but maybe that was taught only in the context of Partial Differential Equations (PDEs), not Ordinary Differential Equations (ODEs). This is still not the mathematics that Keen is claiming that economists mostly do not learn, although it is getting there.
You might also see ordinary differential equations in a numerical analysis course. Here you could learn about, say, the Runge-Kutta method. And the methods here can apply to IVPs for systems of non-linear equations3. I believe in the course that I took, we had a project that began to get at the rudiments of complex systems. I think we had to calculate the period of a non-linear predator-prey system. I believe we might have been tasked with constructing a Poincaré return map.
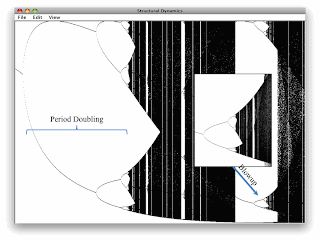
According to Keen, a sufficiently numerate economist should know the theory behind complex dynamical systems, chaos, bifurcation analysis, and catastrophe theory4. I think such theory requires an analysis able to examine global properties, not just local stability results. And one should be interested in the topological properties of a flow, not just the solution to a (small number of) IVPs. Although this mathematics has been known, for decades, to have applications in economics, most economics do not learn it. Or, at least, this is Keen's claim.
Economists should know something beyond mathematics. For example, they should have some knowledge of the sort of history developed by, say, Fernand Braudel or Eric Hobsbawm. And they should have some understanding of contemporary institutions. How can they learn all of this necessary background and the needed mathematics5, as well? I do not have an answer, although I can think of three suggestions. First, much of what economists currently teach might be drastically streamlined. Second, one might not expect all economists to learn everything; a pluralist approach might recognize the need for a division of labor within economics. Third, perhaps the culture of economics should be such that economists are not expected to do great work until later in their lifetimes. I vaguely understand history is like this, while mathematics is stereotypically the opposite.
Footnotes- As a student, I was somewhat puzzled by why my textbooks were always only Introductions to X or Elements of X. It took me quite some time to learn the prerequisites. How could this only be an introduction? Only later work makes this plain.
- Good physics textbook are clear about linear approximations to the sine function for small angles. Although our textbook motivated perturbation theory in the context of models of solar systems, I have never seen perturbation theory applied here in a formal course. Doubtless, astrophysicists are taught this.
- Stiff differential equations is a jargon term that I recall being used. I do not think I ever understood what it meant, but I am clear that the techniques I think I have mostly forgotten were not universally applicable without some care.
- Those who have been reading my blog for a while might have noticed I usually present results for the analysis of non-linear (discrete-time) difference equations, not (continuous-time) differential equations.
- There are popular sciences books about complex systems.