Suggestions For Adding To The Stack

I probably will not order the first two. But I think their existence is of interest. And I do not currently have access to the third.

• Norbert Häring and Niall Douglas (2012) Economists and the Powerful: Convenient Theories, Distorted Facts, Ample Rewards, Anthem Press.
• Kalle Lasn (2013) Meme Wars: The Creative Destruction of Neoclassical Economics, Seven Stories Press.
• Tobias Galla and J. Doyne Farmer (22 January 2013). Complex Dynamics in Learning Complicated Games, Proceedings of the National Academy of Sciences of the United States of America, V. 110, No. 4: pp. 1232-1236
• Sergio Parrinello (2000). The "Institutional Factor" in the Theory of International Trade: New vs. Old Trade Theories.

I suppose I might try to find the paper, by Benjamin Page, Larry Bartels, and Jason Seawright, that Paul Krugman references in his New York Times column last Friday. By the way, Krugman is basically worrying that economics is "vulgar political economy", a technical term introduced by Karl Marx. But Krugman cannot reference Marx or acknowledge Marx was maybe correct about something.

In my draft paper on the failure of the theory of comparative advantage to justify free trade, I am currently ignoring Krugman and new trade theory. The fourth reference above might be usefully footnoted in my article. I believe Parrinello also has an article in a recent festschrift volume for Ian Steedman.

I recently stumbled across Rob Beamish's 1992 book, Marx, Method, and the Division of Labor. This book traces the development of a concept, the division of labor, in Marx's manuscripts and published work, including the manuscripts I mentioned in a previous post. Furthermore, Beamish argues that if historical materialism is true, it must apply to the development of Marx's ideas.

Choice of Technique, A Two Good Model, Cobb-Douglas Production Functions

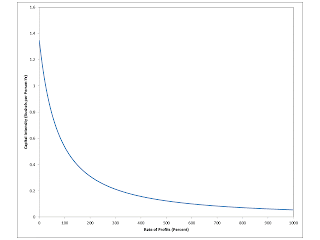
Figure 1: Wage-Rate of Profits Curves and their Frontier

1.0 Introduction

This post is a generalization of a neoclassical one-good model. It advances a comparison of Sraffian analysis of the choice of the cost-minimizing choice of the technique and neoclassical analyses, correctly understood, of marginal productivity. Accordingly, all production functions are smooth in this example. If substitutability is seen as a technological property of production functions, then the single capital good and labor can be substituted in each of the two industries in this model.

2.0 The Technology

Consider a simple economy in which steel and corn are produced from inputs of steel and labor. The steel used as an input in production is totally used up in yearly cycles, and the outputs become available at the end of the year. In other words, this is a model without fixed capital, and all production processes require a year to complete.

2.1 Production Functions

The production function for steel is:

Q₁ = F₁(X₁, L₁) = A₁ X₁^α₁ L₁^{(1 - α₁)}

where:

• Q₁ is (gross) output of steel (in tons).
• X₁ is steel (tons) used as a capital good in the steel industry.
• L₁ is labor (person-years) used as an input in the steel industry.

and A₁ and α₁ are positive constants such that:

0 < α₁ < 1

The production function for corn is:

Q₂ = F₂(X₂, L₂) = A₂ X₂^α₂ L₂^{(1 - α₂)}

where:

• Q₂ is (gross) output of corn (in bushels).
• X₂ is steel (tons) used as a capital good in the corn industry.
• L₂ is labor (person-years) used as an input in the corn industry.

and A₂ and α₂ are positive constants such that:

0 < α₂ < 1

2.2 A Set of Coefficients of Production

An alternative specification of this Constant-Returns-to-Scale (CRS) technology is as a set of coefficients of production a₀₁(s₁), a₀₂(s₂), a₁₁(s₁), a₁₂(s₂) from the set:

{ (a₀₁(s₁), a₀₂(s₂), a₁₁(s₁), a₁₂(s₂)) | 0 < s₁, 0 < s₂}

where:

a₀₁(s₁) = [1/(A₁s₁)]^{[1/(1 - α₁)]}

a₀₂(s₂) = [1/(A₂s₂)]^{[1/(1 - α₂)]}

a₁₁(s₁) = s₁^(1/α₁)

a₁₂(s₂) = s₂^(1/α₂)

and

• a₀₁(s₁) is the labor required, in the steel industry, per ton steel produced.
• a₀₂(s₂) is the labor required, in the corn industry, per bushel corn produced produced.
• a₁₁(s₁) is the steel input required, in the steel industry. per ton steel produced (gross).
• a₁₂(s₂) is the steel input required, in the corn industry, per bushel corn produced.

2.0 Quantity and Price Equations, Given the Technique

Consider a stationary state in which the firms employ one person-year of labor each year, and prices are stationary. For notational convenience below, define the following function:

f(R) = (a₀₁a₁₂ - a₀₂a₁₁)R + a₀₂

2.1 Quantity Relations

The amount of steel produced each year, measured in tons, is:

q₁ = a₁₂/f(1)

The amount of corn produced each year, measured in bushels, is:

q₂ = (1 - a₁₁)/f(1)

These quantities must satisfy two equalities. First, the amount of labor employed is unity:

1 = a₀₁q₁ + a₀₂q₂

Second, consider the following equation:

q₁ = a₁₁q₁ + a₁₂q₂

The left-hand side of the above equation denotes the quantity of steel produced each year and available, as output from the steel industry, at the end of each year. The right-hand side denotes the sum of steel used as inputs in the steel and corn industries, respectively. These inputs must be available at the start of each year. Hence, the above equation is a necessary condition when the economy is in a self-sustaining, stationary state.

2.2 Price Relations

I take the consumption good, corn, as the numeraire. The price of steel, in units of bushels per ton, is

p = a₀₁/f(1 + r),

where r is the rate of profits. The wage is:

w = [1 - a₁₁(1 + r)]/f(1 + r)

The above equation is known as the wage-rate of profits curve.

The price of steel, the wage, and the rate of profits must satisfy two equations. The condition that the price of steel just cover the cost of producing steel is:

pa₁₁(1 + r) + a₀₁w = p

The left-hand side of the above equation shows the cost of producing a ton of steel. Costs are inclusive of normal profits, so to speak, on the cost advanced to purchase physical inputs at the start of the year. In this case, those inputs consist of steel, the single capital good in this model. Although labor is hired at the start of the year to work throughout the year, the price equations in this model show labor being paid out of the harvest gathered at the end of the year.

The condition that the price of corn just cover the cost of producing corn yields a similar equation:

pa₁₂(1 + r) + a₀₂w = 1

2.3 The Capital-Labor Ratio

"Capital" is an ambiguous term. It denotes both physically-existing means of production. And it denotes the value of those means of production, when embedded in certain social relations. For example, in this model, the distribution of the capital goods over the two industries is assumed to be appropriate to the continued self-reproduction of the economy. In a sense, the plans of entrepreneurs and firms managers are coordinated.

At any rate, the relationships described so far allow one to express the value of capital, in numeraire units, per person-years, given the technique:

k = p q₁

k = a₀₁a₁₂/[f(1)f(1 + r)]

The capital-labor ratio (in units of bushels per person-years) does not appear in any legitimate marginal product. Nevertheless, I find it a useful quantity for further analysis in multicommodity models.

3.0 The Chosen Technique

The cost-minimizing technique differs with the rate of profits. For analytical convenience, I take the rate of profits as exogenous in this model. One could, instead, if one so chose, take the wage as given and find the rate of profits endogenously. At any rate, this model is open, and the distribution of income is not determined in the model. The equations below set out each of the four coefficients of production in this model as functions of the rate of profits:

a₀₁ = (1/A₁)^{[1/(1 - α₁)]} [(1 + r)/α₁]^{[α₁/(1 - α₁)]}

a₀₂ = (1/A₂)

x {(1 - α₂)/[(α₁)^{[α₁/(1 - α₁)]}(1 - α₁)α₂]}^α₂

x [(1 + r)/A₁]^{[α₂/(1 - α₁)]}

a₁₁ = α₁/(1 + r)

a₁₂ = (1/A₂)

x [(α₁)^{[α₁/(1 - α₁)]}(1 - α₁)α₂/(1 - α₂)]^{(1 - α₂)}

x [A₁/(1 + r)]^{(1 - α₂)/(1 - α₁)}

3.1 Steel as a Basic Commodity and the One-Good Case

I have previously set out an analysis of the choice of technique for a one-good model with an aggregate Cobb-Douglas production function. In the two-good model set out in this post, the coefficients of production for steel, a₀₁ and a₁₁, when the cost-minimizing technique is chosen, are the same as the coefficients of production in that one-good model. This is not surprising.

In the model in this post, steel enters, as an input, into the production of both steel and corn, for all possible techniques. On the other hand, corn never enters as an input into the production of any commodity. In the technical terminology of post-Sraffian economics, steel is always a basic commodity, and corn is never a basic commodity. Thus, the production of steel can be analyzed, in some sense, prior to the analysis of the production of corn.

3.2 A One-Good Special Case

Consider the special case in which:

α₁ = α₂ = α

A₁ = A₂ = A

In effect, steel and corn are the same commodity. The coefficients of production, for the cost-minimizing technique are:

a₀₂ = a₀₁ = (1/A)^{[1/(1 - α)]} [(1 + r)/α]^{[α/(1 - α)]}

a₁₂ = a₁₁ = α/(1 + r)

So this case reduces to the one-good model, as it should. This concludes my analysis of this special case.

4.0 The Chosen Technique on Unit Isoquants and Marginal Productivity Conditions

The coefficients of production are such that the steel industry lies on its unit isoquant:

1 = F₁(a₁₁, a₀₁)

Likewise, the corn industry lies on its unit isoquant:

1 = F₂(a₁₂, a₀₂)

Since the coefficients of production in Section 3 above are for the cost-minimizing technique, all valid marginal productivity relationships must hold. I have chosen to express each marginal productivity condition in numeraire units per unit input. And, the cost of an input and its marginal product are equated here at the end of the year.

Following these conventions, the following display equates the cost of steel to the value of the marginal product of steel in the steel industry:

p(1 + r) = p ∂F₁(a₁₁, a₀₁)/∂a₁₁

Likewise, the following display equates the cost of steel to the value of the marginal product of steel in the corn industry:

p(1 + r) = ∂F₂(a₁₂, a₀₂)/∂a₁₂

Since wages are paid out of the harvest, the rate of profits does not appear in my statement of marginal productivity conditions for labor. The following display equates the wage and the value of the marginal product of labor in the steel industry:

w = p ∂F₁(a₁₁, a₀₁)/∂a₀₁

Likewise, the following display equates the wage and the value of the marginal product of labor in the corn industry:

w = ∂F₂(a₁₂, a₀₂)/∂a₀₂

I have checked the above equations for the isoquants and the four marginal productivity equations. This is quite tedious.

Above, I have listed six equations, two expressing the condition that the coefficients of production lie upon unit isoquants and four marginal productivity equations. These six equations are sufficient to determine the six unknowns (w, p, a₀₁, a₀₂, a₁₁, and a₁₂) in terms of the model parameters and the externally specified rate of profits. In other words, this model illustrates that marginal productivity is a theory of the choice of technique, not of the (functional) distribution of income.

5.0 The Wage-Rate of Profits Frontier

An alternate analysis of the choice of technique can be based on the wage-rate of profits frontier. And this analysis yields the same answer as the above analysis based on marginal productivity.

Recall, from Section 2.2, that a technique can be specified as an ordered pair chosen from the specified index set. The index variables for the cost-minimizing technique, as a function of the rate of profits are:

s₁ = [α₁/(1 + r)]^α₁

s₂ = (1/A₂)^α₂

x [(α₁)^{[α₁/(1 - α₁)]}(1 - α₁)α₂/(1 - α₂)]^{[(1 - α₂)α₂]}

x [A₁/(1 + r)]^{[(1 - α₂)α₂/(1 - α₁)]}

I think it of interest to note that both the optimal process for producing steel and the optimal process for producing corn, in a stationary state, vary continuously with the rate of profits. This is not a generic result for a discrete technology. In a discrete technology, the cost-minimizing techniques at a switch point typically differ in the process used in only one industry; a small variation in the rate of profits thus affects only the specification of a process in one industry.

5.1 First Order Conditions

Since the coefficients of production are functions of the index variables, the wage-rate of profits curve for a technique can be viewed as a function of:

• The index variables s₁ and s₂,
• The rate of profits r, and
• The model parameters α₁, A₁, α₂, and A₂.

A necessary condition for a technique to be cost-minimizing, at a given rate of profits, is that the wage be a maximum. This maximum is taken from the wage on each wage-rate of profits curve, over all techniques. In the current context, with a model with smooth production functions, the first derivative of the wage-rate of profits frontier, with respect to each index variable, must be zero at the maximum:

∂w/∂s₁ = 0

∂w/∂s₂ = 0

Note that the above is a system of two equations in the two unknown index variables. I did not actually calculate the above derivatives for this model. Perhaps Figure 1 provides some confidence in this mathematics. I deliberate drew three wage-rates of profits curves on the frontier and one off of it.

5.2 Second Order Conditions

The FOCs determine a critical point. The calculus is consistent with such a critical point being a local maximum, a local minimum, or a saddle point. The following are sufficient conditions, in this context, for a critical point to be a local maximum:

∂²w/∂s₁² < 0

∂²w/∂s₂² < 0

D(s₁, s₁) > 0

where D(s₁, s₁) is defined by:

D(s₁, s₁) = [∂²w/∂s₁²][∂²w/∂s₂²] - [∂²w/∂s₁∂s₂]²

Of the three SOCs, either the first or the second is redundant.

6.0 Conclusion

I still have some ideas for future work with this model. But I think this is enough for one blog post. I hope the above presentation suggests that marginal productivity is not a theory of distribution, in general. One cannot validly hold, for example, that real wages are determined by the marginal product of labor. Furthermore, the Sraffian analysis of the choice of technique is analytically equivalent to the determination of the choice of technique, given, for example, the rate of profits, by marginal productivity.

Who Is Joshua Clover?

Joshua Clover has a great one-page article on Krugman in this week's Nation. I'd like to quote the whole thing. But I'll make do with extracts:

"Consider the phenomenon of Paul Krugman, of late taking a curious turn... ...Krugman [is] advantageous[ly] position[ed] as a public intellectual famously handy with hard data and rigorous analyses. Ask Thomas Friedman: anyone can be a blowhard on matters global. Few can do the math.

...as a star economist, [Krugman's] historical role has been to reinvigorate the duel between liberal Keynesians and the recently regnant monetarists of various stripes...

...For the record, I greatly preferred the Backstreet Boys to 'N Sync...

The oppositions Republican/Democrat and monetarist/Keynesian are in this regard pure pop. They are, as you will have noticed some time ago, choices only in the most straitened sense: minimally distinct management strategies for capitalism. Their present distinction lies in whether crisis is best managed by allowing the owners of capital everything they want immediately, or at pace lest they choke on something...

And yet. In December, Krugman wrote two blog entries in swift succession: 'Rise of the Robots' and 'Human Versus Physical Capital'. Inequality, his charts informed him, was itself a consequence of the opposition between capital and labor—specifically the increasing domination of capital in the form of machines—as labor is expelled from the production process. That ratio turns out to be basically the same measure as productivity, sine qua non of economic progress.

Moreover, in a development Krugman couldn't quite bring himself to declare, his charts suggest that a generally declining labor share since the 1970s has also spelled bad news for overall profitability outside the finance sector. The productivity race wasn't just unfortunate for the unemployed; it was for capital a poison pill of its own making. Thus Krugman's comedy: always on the verge of discovering the arguments of a 150-year-old book; always turning away at the last second. In Krugman's words, 'I think our eyes have been averted from the capital/labor dimension of inequality, for several reasons. It didn't seem crucial back in the 1990s, and not enough people (me included!) have looked up to notice that things have changed. It has echoes of old-fashioned Marxism—which shouldn't be a reason to ignore facts, but too often is. And it has really uncomfortable implications.'

Does it? I suppose so. And that uncomfort is what pop, for all its pleasures, must defer. Pop must affirm the way things are, no matter how often it choruses the word 'change.' You cannot be Paul Krugman, Pop Star, and at the same time discover that capital is built to break us, and itself—even if your charts so testify. So you will not be shocked to discover Krugman stepped back from this realization and continued about his business, scarcely speaking of it again. There are some things you do not say. They are not popular."

"Technology and Wages, the Analytics" was another Krugman post in the same period, along the same lines. I've already commented on that one.

Choice Of Technique With A Smooth Aggregate Production Function

Figure 1: Coefficients of Production for the Technology

1.0 Introduction

This post advances, somewhat, my start at a reconsideration of the dynamics of Overlapping Generations Models (OLGs). Only the production side of a stationary state is considered here. Furthermore, only a very special case - namely, a one-good model - is analyzed here.

I guess the most exciting aspect of this post is an illustration of the claim that the construction of the wage-rate of frontier is useful for the analysis of the choice of technique for "smooth" production functions, not just for discrete technologies. I have never understood, for at least a quarter of a century, why some economists seem to talk as if a fundamental distinction exists between such models. In some contexts, some conclusions differ. But it seems to me to be silly to say that the Cambridge Capital Controversy turns around an empirical question on the degree of substitutability of inputs in production.

2.0 Specification of Technology

Consider a simple economy in which corn is produced from inputs of labor and corn. Assume the existence of Constant Returns to Scale (CRS). A technique is specified by an ordered pair of coefficients of production, where each ordered pair is from a set containing a continuum of such ordered pairs:

{ [a₀(s), a₁(s)] | 0 < s < 1}

where:

a₀(s) = 1/(A s)^{1/(1 - α)}

a₁(s) = s^1/α

and α and A are specified positive parameters such that:

0 < α < 1

Figure 1 graphs the coefficients of production as a function of the index s. All graphs are draw for a value of α of 1/4 and of A of 5.

3.0 Derivation of the Cobb-Douglas Production Function

The above specification of the technology shows, for a unit output of corn, a smooth trade-off of inputs of labor and corn inputs. This specification of technology allows for the derivation of a conventional production function. The following is an equation for a unit isoquant for this technology:

1 = A [a₁(s)]^α [a₀(s)]^{1 - α}

Define:

• Q is (gross) corn (bushels) output.
• L is labor (person-years) input.
• X is (seed) corn input.

From CRS, it follows:

Q = A [Q a₁(s)]^α [Q a₀(s)]^{1 - α}

Or:

Q = A X^α L^{1 - α}

The last equation above is how the (in)famous Cobb-Douglas production function is typically represented. So the specification of technology used in this post is a (non-unique) representation of a Cobb-Douglas production function.

4.0 Analysis of the Choice of Technique

For a given technique, Sraffa's price equations become one equation:

a₁(s)(1 + r) + a₀(s) w = 1

where:

• r is the rate of profits
• w is the yearly wage (in units of bushels per person-year).

The price equation embeds the assumptions that production of corn requires a year to complete and that labor is paid out of the yearly harvest. One can derive a wage-rate of profits curve from the price equations:

w(r, s) = [1 - a₁(s)(1 + r)]/a₀(s)

In this case, each wage-rate of profits curve is a straight line. Figure 2 shows three selected wage-rate of profits curves.

Figure 2: Wage-Rate of Profits Curves and Their Frontier

Figure 2 shows, in violet, the outer wage-rate of profits frontier. When firms choose the cost-minimizing technique in a steady state, the economy will lie on this curve. (In this case, with a continuum of techniques, each point on the frontier is a non-switch point.) A closed-form expression for the wage-rate of profits frontier is easily derived. The First Order Condition (FOC) for the choice of technique can be expressed as equating the derivative, with respect to the index variable, of the wage-rate of profits curve to zero:

dw/ds = 0

The FOC yields an equation which can be solved for the index variable:

s(r) = [α/(1 + r)]^α

So the coefficients of production, for the cost-minimizing technique, can be found as functions (Figure 3) of the rate of profits:

a₀(r) = [1/A^{1/(1 - α)}] [(1 + r)/α]^{α/(1 - α)}

a₁(r) = α/(1 + r)

Thus, the desired expression for the wage-rate of profits frontier is:

w(r) = (1 - α) A^{1/(1 - α)} [α/(1 + r)]^{α/(1 - α)}

In this special case, the desired amount of labor per unit output is higher, the lower the wage. Likewise, the desired amount of the capital good per unit output is lower, the higher the rate of profits. These results do not generalize to multi-commodity models.

Figure 3: Optimal Coefficients of Production

5.0 Capital Intensity

In this special case, the ratio of the value of capital goods to labor can be calculated in physical terms, without addressing a question of valuation. That is, the capital-labor ratio, as a function of the rate of profits (Figure 4), is easily derived:

I(r) = a₁(s(r))/a₀(s(r)) = [α A/(1 + r)]^{1/(1 - α)}

In this special case, the capital-labor ratio is a downward-sloping, single-vauled function of the rate of profits. These properties do not generalize, either.

Figure 4: Capital Intensity

"Economics Textbooks - Decades of Scientific Fraud"

Lars Syll has written a post, titled "Economics Textbooks - Decades of Scientific Fraud". If you had not already read it, could you guess what it is about from the title?

I would expect likely guesses to be non-unique. It is not about:

• How the Cambridge Capital Controversy demonstrates that textbook teaching on labor markets and, for example,on the minimum wage is nonsense.
• The incoherence of textbook teaching on the justification for lack of tariffs by the theory of comparative advantage.
• The textbook misrepresentations of the theories of various economists, including John Maynard Keynes.

You can extend the above list at your leisure.

In many ways, economics seems to me to be an extraordinary subject. Good arguments have existed for decades for discarding most of mainstream teaching and practice. As far as I can see, the bulk of these arguments, including their very existence, are just ignored by most mainstream economists. I am willing to entertain demonstrations of the fallacy of theories taught in almost all mainstream textbooks for decades. I think my willingness to explore other demonstrations than those I have been previously aware of is partly due to my belief that most economists are socialized into willful ignorance.

I can see why some young mainstream economists may resist the notion that they have been taught, mostly, lies and nonsense. And so they may look in the research literature for arguments against the arguments and demonstrations that I accept, or at least try to explore. Since my favorite positions were established after long controversy, you can find neoclassical counter-arguments, of a sort. For example, one might cite, in response to the Cambridge Capital Controversy:

• Edwin Burmeister's championing of Champernowne's chain index measure of capital¹.
• Frank Hahn's advocacy, including in response to the Cambridge Capital Controversy, of General Equilibrium Theory².

In response to the application of the CCC to the theory of international trade, one might cite:

• Christopher Bliss's suggestion that the necessary existence of gains from trade follows from including an assumption that all produced goods, not just consumer goods, be traded internationally.
• Wilfred Ethier's claim that the endowment of capital be calculated in equilibrium prices in models of international trade.
• A suggestion that the theory of international trade be organized around comparisons of intertemporal equilibrium paths³.

One might think a conclusion is more justified from the weight of the evidence when multiple arguments reach that conclusion. So one might react to existence of such controversies in the research literature as allowing one to support mainstream teaching. However, one would be wrong in this attitude. If you look at these responses in some detail, you will find that the orthodox economists do not end up at the textbook position, but at some other point. But, as far as I can tell, neither side ends up being transitioned from the research literature to conventional teaching. Would you not be more confident in adopting some such conventional counter-argument to one of my favorite arguments if it were widely taught? Otherwise, should you not suspect yourself of adopting an idiosyncratic misinterpretation of the theory?

Footnotes

1. This chain index is endogenous, not exogenous, as needed for much of neoclassical theory. Furthermore, Burmeister accepts the validity of demonstrations of reswitching and capital-reversing.
2. A focus on intertemporal and temporary equilibria is a rather drastic change of theory from the traditional neoclassical focus on a comparison of long run equilibria. The latter comparisons seem to be to provide the (exploded) foundation for most mainstream policy advice.
3. Avinash Dixit (May 1981). The Export of Capital Theory, Journal of International Economics. V. 11, Iss. 2: pp. 279-294.

Perfect Competition Is The Same As Monopoly If You Do The Math Right

1.0 Introduction

This post summarizes one aspect of a theorem presented and proved by Roy Radner (1980). I have previously expressed skepticism about the claim in the post title. I have also heard that, in game theory, anything can happen, but nothing need happen. So, I suppose, one should not be surprised in stumbling over a proof of the existence of almost any market behavior in the literature on game theory. But I was surprised.

2.0 Selected Assumptions

2.1 Non-Cooperative Firms

In the model considered here, no mechanism exists to enforce agreements among firms. In the jargon, only (extensions of) Cournot-Nash equilibria are considered here.

2.2 Firm Managers Making Approximately Optimal Output Decisions

Although not commonly stated, the textbook presentation of perfect competition assumes the managers of the firms are systematically mistaken about their optimum decisions. A homogeneous product is assumed to be produced by a finite number of firms in the industry, and the total industry output is finite. Managers are assumed to disregard any strategic reaction by other firms to variation in their own firm's output and to take the price of their product as given. But, for a given consumer demand function, the firm's (notional) variation in output results in a variation in prices. So the decisions of the managers can only be approximately optimal, in textbook theory.

Radner proposes the notion of an epsilon-equilibrium to formalize this idea that firm strategies are only approximately optimal. In such an equilibrium each firm's strategy is such that, for example, average profit is within epsilon of the maximum average profit achieved by an optimal strategy, given the strategies of all other firms. As is typical in mathematical analysis, one should think of ε as a given (small) parameter.

2.3 Sequential Market Interactions

Firms are not considered as deciding on a single quantity to produce in this model. Rather, each firm decides on a sequence of T quantity outputs, one for each of T successive periods. The parameter T is known as the lifetime of the industry. Each firm decides on the output in a given period as a function of the outputs of all firms in all previous periods. A strategy is a sequence of such functions, one for each firm. The firm chooses a strategy to maximize its average or total discounted profit over the lifetime of the industry.

2.4 Replication

The theorem outlined here is used to compare epsilon-equilibria for different (finite) numbers of firms in the industry. Radner defines the replication case to apply when the demand price is an unchanged function of the average output per firm. In some sense, the number of consumers increases, in the model, with the number of firms.

3.0 An Informally Stated Theorem

Theorem: Consider the model with the above assumptions. Let the number of firms increase, along with the lifetime of the industry, such that the number of firms remains small enough, when compared to the lifetime of the industry. For any finite number of firms, equilibria exist in which the firms act as a cartel, and the cartel lasts for any given duration, provided the lifetime of the industry is taken large enough.

4.0 Conclusion

I think of the point of this post to explore the result of tweaking textbook assumptions in the theory of perfect competition. Apparently, the results are sensitive to the exact statement and combination of assumptions. I gather that further research in microeconomic theory has confirmed that whether or not equilibria converge, as the number of firms increase, to the perfect competition model is a fine point. That is, equilibria may or may not converge to a model with a continuum of firms. Radner seems to feel exploring certain sets of assumptions is of more interest than other sets. I have chosen to emphasize a set of assumptions in which any finite number of firms may act like a monopoly, in a precise sense.

Another approach might be better in empirically describing firms in actually-existing capitalism.

Reference

• Roy Radner (1980). Collusive Behavior in Noncooperative Epsilon-Equilibria of Oligopolies with Long but Finite Lives, Journal of Economic Theory, V. 22: pp. 136-154

A Numeric Example Of The Loss From Trade

Ratio of the Value of Capital to Labor

This post summarizes a numeric example in which at least one country is unambiguously worse off under free trade. This example illustrates the model I developed in a draft paper. The example in this post differs from the one in my paper; interest rates of concern here are more reasonable values.

The model is of two small open economies facing identical technologies for producing two consumer goods. The model assumptions are:

1. Two countries, A and B, can produce the same two commodities, wine and silk, for consumption.
2. The entrepreneurs in each country know the given flow-input, point-output technology (Table 1). Wine and silk each require two years of labor input per unit output. For example, the grapes for a unit of wine require 10 person-years of unassisted labor to be expended in the first year. One hundred eighty eight person-years of labor work up these grapes into wine produced for consumption at the end of the second year.
3. Each country has a given endowment of labor, the only non-produced factor of production in each country. The labor force is fully employed in each country.
4. Only commodities produced for consumption can be traded internationally. Laborers neither immigrate nor emigrate. Capital cannot be traded internationally.
5. Wine and silk are produced with different factor-intensities, silk being more capital-intensive and wine being more labor-intensive. No factor-intensity reversals exist.
6. All consumers, in all countries, have identical homothetic utility functions.
7. Perfect competition obtains in all markets; transport costs are negligible; and free trade exists in all commodities produced for consumption, unless otherwise specified.

These are textbook assumptions. The numeric example proves mainstream textbooks are simply incorrect, since the opposite answer is obtained.

Table 1: The Technology

	Country A	Country B
Wine Production	l1,A = 10 person-yrs per unit wine	l1,B = 10 person-yrs per unit wine
	l2,A = 188 person-yrs per unit wine	l2,B = 188 person-yrs per unit wine
Silk Production	l3,A = 100 person-yrs per unit silk	l3,B = 100 person-yrs per unit silk
	l4,A = 89 person-yrs per unit silk	l4,B = 89 person-yrs per unit silk
Endowments	lTotal,A = 4,158 person-years	lTotal,B = 3,969 person-years

The firms in both countries face given prices of wine and silk on the international market, as shown in Table 2. The domestic interest rate and the corresponding wage vary between the two countries. As shown in my paper, one can use this price system to determine which commodity, if any, firms in each country would find it most profitable to specialize in the production of. If the interest rate were zero, each country would attempt to specialize in the producing silk. For the price of silk to be a switching price, where firms would find it profitable to specialize in the production of both wine and silk, the interest rate must be 10% for the example. For the interest rates shown, country A specializes in the production of wine, and country B specializes in the production of silk.

Table 2: The Selected Price System

	Country A	Country B
Price of Silk:	p = 1 units wine per unit silk
Interest Rate:	rA = 20%	rB = 5%
Wage:	wA = (1/200) units wine per person-yr	wB = (1/194) units wine per person-yr

Given the technology, endowments, an equilibrium price system, and tastes, one can calculate how much wine and silk will be produced and consumed in each country, both when neither country can trade consumer goods on international markets and when both can. Table 3 shows the resulting patterns of consumption among stationary states in the two countries. The consumers in country A are unambiguously worse off in a stationary state with specialization and free trade.

Table 3: Results for the Numeric Example

		Autarky	Specialization
Wine Consumption	Country A	10 1/2 Units wine	10 1/2 Units wine
	Country B	10 1/44 Units wine	10 1/2 Units wine
	Total	20 23/44 Units wine	22 Units wine
Silk Consumption	Country A	11 Units silk	10 1/2 Units silk
	Country B	10 1/2 Units silk	10 1/2 Units silk
	Total	21 1/2 Units silk	22 Units silk

Figure 1, constructed for the example, shows that the endowment of capital cannot be taken as a parameter in the illustrated model. Because of price Wicksell effects, the quantity of capital varies with the interest rate, even for a given pattern of specialization. Yet confused textbook writers often present the Heckscher-Ohlin-Samuelson model in a two-country, two-commodity, two-factor framework, with the factors of production incorrectly labeled as "labor" and "capital".

So much for the orthodox theory of free trade. Neo-Ricardians proved, more than a third of century ago, that the neoclassical theory of international trade is defective in other ways, too.

Political Elites Bowing Down Before The Ones They Serve

Table 1: Politicians in State Legislatures Ignorant of Strength of Constituent Support for Universal Health Care

Table 2: Politicians in State Legislatures Ignorant of Strength of Constituent Support for Gay Marriage

In 2012, Broockman and Skovron surveyed candidates for office in state legislatures throughout the United States. Nearly 2,000 candidates replied. About half of those responding won their races, about half are Democrats, and about half are Republicans. The survey asked the respondents to estimate their constituents' support for the following three policy proposals:

• Implement a universal healthcare program to guarantee coverage to all Americans, regardless of income.
• Same sex couples should be allowed to marry.
• Abolish all federal welfare programs.

Broockman and Skovron also estimated the actual support for these proposals in each of the respondents' districts. Estimates of actual support come out of a multi-level regression and poststratification (MRP) model. The paper contains a neat map of greater Los Angeles showing the results of the MRP model for districts there.

Figures 1 and 2, above, compare the actual support for the first two policy proposals, respectively, to estimated support. If estimates matched actual values, they would lie on the 45 degree line, shown in grey on the graphs. A striking finding is that members of state legislatures tend to think their districts are more conservative than they are. The bias is more extreme for conservative politicians: "Nearly half of sitting conservative officeholders appear to believe that they represent a district that is more conservative ... than the most conservative legislative district in the entire country." Furthermore, politicians learn next to nothing about their constituents' views in running for office.

Broockman and Skovron use these results as a starting point for speculating on how constituents can control their representatives, given these systematic biases in the representatives understanding of opinions among their constituents. As I understand it, this approach fits into a large question within political science, as studied in the United States: How can democracy work even as good as it does in the United States, given the widespread ignorance of the most basic facts about the political system on the part of populace in the United States, including voters? Broockman and Skovron have added a new question: How can democracy work in the United States, given not only ignorance among the populace, but also systematic ignorance on the part of elected officials?

I would like to suggest two hypotheses for explaining these results. First, I suggest legislatures are accurately reflecting the views of their constituents, at least those constituents who matter. Martin Gilens finds that only the policy views of the rich influence what policy gets implemented, at least on the Federal level. Andrew Gelman has shown that the rich tend to be more reactionary in their views.

Second, I would like to suggest that norms of politeness in the United States interacts with conservative minds such that conservatives are systematically underexposed to liberal views among their constituents. I draw on Jonathan Haidt's work here. In some work, he defines five dimensions of moral intuitions:

1. Harm/care
2. Fairness/reciprocity
3. In-group/loyalty
4. Authority/respect
5. Purity/sanctity

(Quite a bit of literature exists on the different cognitive styles of conservatives and liberals. Liberals tend to have more activity in the anterior cingulate cortex, and conservatives tend to have a more active amygdala.) Liberals tend to worry more about harm and fairness, while conservatives equally emphasize all five dimensions.

My hypothesis is that conservatives tend to hear those articulating liberal, or even more left views, as being rude. If you are not comforting the comfortable, these days, you are branding yourself as not a member of an in-group that conservatives are loyal to, showing disrespect for our elites, and demonstrating personal impurity. So whether or not they understand liberal views, conservatives are unlikely to perceive such views as any more than eccentricities.

I suppose one could test my first hypothesis by comparing politicians' estimates of their constituents' views with the actual views of those constituents in the top 10% or 1%, by income or wealth. I'm not sure how one would empirically assess my second hypothesis, relating norms of politeness to political views. However one did this, I would think my second hypothesis would apply in a more extreme fashion to rural districts, as compared with urban districts. I do not know how this would apply in suburban districts.

I've probably made my usual share of spelling and grammar mistakes above. But I get to conclude this post, as if it were a journal publication, not a off-the-cuff blog post. More research is needed.

References

• David E. Broockman and Christopher Skovron. What Politicians Believe About Their Constituents: Asymmetric Misperceptions and Prospects for Constituency Control, Working Paper (3 March 2013).
• Andrew Gelman. Red State, Blue State, Rich State, Poor State: Why Americans Vote the Way They Do. [I HAVE ONLY READ PAPERS SUMMARIZING THIS]
• Martin Gilens. Affluence and Influence: Economic Inequality and Political Power in America, Princeton University Press (2012). [I HAVE ONLY READ A GILENS PAPER, NOT THIS BOOK]
• Jesse Graham, Jonathan Haidt, and Brian A. Nosek. Liberals and Conservatives Rely on Different Sets of Moral Foundations (2009).
• Jonathan Haidt. The Righteous Mind: Why Good People are Divided by Politics and Religion, Vintage (2013). [I HAVE ONLY READ PAPERS SUMMARIZING THIS]