Old Findings For New Times

From John Kenneth Galbraith's The Affluent Society (1958), I know that widespread attitude to waged work among some in the United States is outdated. The conventional wisdom is that work is necessary because it is needed to produce the goods that sustain society. That was largely true before productivity increased so much, for example, in the post war golden age. Some jobs are still essential, by any narrow definition, but much wage work goes to creating goods and services that in any previous society would have been considered useless luxuries. (As I get older though, I disagree with Galbraith about medicines to improve peristalsis.) But waged work, in the current system, is essential for providing the income needed to sustain the demand to keep the system going.

From Paul Davidson and Joan Robinson, I know about the distinction between historical and logical time. It as not as if the economy is in an equilibrium that will be approached again, and quickly, after a downward shock is removed. People will recall, and those who are out of work will try to cut back their spending. States and localities that have had to increase their spending to address such a shock will need to retain the ability to spend, and even to increase spending.

From Michal Kalecki's "Political aspects of full employment" (1943), I know that the ruling bourgeois class cannot be counted on to support what is even in their immediate short term financial interest. Unemployment is convenient for keeping the mass majority of the population, the labor force, cringing and hard to press for more of a share in the commodities that they produce. Even so, the backwardness of politics in the United States these days is hard to explain.

From Hannah Arendt's Eichmann in Jerusalem (1963), I know that one strategy in implementing totalitarianism is to declare a marginal group stateless, outside your laws and international laws. Refugees and immigrants are one such group that one could try to apply this strategy to, if you are for evil. From Carl Schmitt's The Concept of the Political (1932), I know that sovereign is he who can declare the state of exception. I resent that these ideas are relevant today.

A Fluke Switch Point On The Wage Frontier

Figure 1: A Switch Point On The Wage Frontier with Wage Curves Tangent

This post extends the example in my article in Structural Change and Economic Dynamics, suitably emended.

Figure 2 shows an enlargement of part of the parameter space. The parameters of the point where the boundaries of Regions 1, 2, and 3 intersect are shown. In Region 1, the Beta technique is uniquely cost-minimizing for all feasible wages; there are no switch points. Region 2 is a reswitching example, with Beta cost-minimizing at low and high wages. One switch point exists in Region 3, with the Beta technique cost-minimizing at low wages.

Figure 2: Part of Parameter Space

The boundary between Regions 1 and 2 is tangent to the boundary between Regions 1 or 2 and Region 3. In what I am calling a reswitching pattern, the scale factor for the rate of profits is found as a double root for a polynomial equation. I have extended the boundary between Regions 1 and 2, with the dotted line, to show where this double root occurs with a negative scale factor for the rate of profits.

Figure 1, at the top of this post, shows wage curves for the example for the parameter values noted in Figure 2. (I used Octave to help with my arithmetic.) The Beta technique is cost-minimizing for all feasible wages. When the wage is at its maximum, the Alpha technique is also cost minimizing. And, at the switch point, the two wage curves are tangent. This is a fluke switch point twice over.

This sort of fluke switch point cannot be expected to be found in empirical data from, say, National Income and Product Accounts. The fluke cases I have been developing are important in that they illustrate partitions in a parameter space for certain models of the choice of technique. They arise as certain characteristics of markets vary with a perturbation of model parameters.

I am not sure what to make of structures within the parts of the parameter space I have been exploring. If you think about, you can see why that must be a point of tangency in Figure 2. Maybe the most striking structure I have found is parallel lines for partitioning a parameter space associated with an example of Harrod-neutral technical change.

I write this stuff as escapism. A lot of economists I build on are in Italy, which is a worrisome place to be these days. I hope you are doing well.

A Fluke Case With Two Fluke Switch Points

Figure 1: Switch Points On The Axis For The Rate Of Profits And At r = -100 Percent

This is an example of a fluke case in the analysis of the choice of technique. The interest in flukes, for me, is that they show how the characteristics of markets can change. They provide insight into structural economic dynamics, as Luigi Pasinetti calls it.

I have previously shown a fluke case, with a switch point on the axis for the rate of profits with a real Wicksell effect of zero. A perturbation of the example can lead to a reswitching example. The switch point at a wage of zero (when the workers live on air) then becomes one at a positive wage. And around that switch point, a higher wage is associated with cost minimizing firms hiring more workers to produce a given net output.

In the example in this post, the switch point on the axis for the rate of profits exhibits neither a forward nor a reverse substitution of labor. The labor coefficient in the corn industry does not vary with the processes in the technique. The Alpha technique has a ghostly presence. It can only be chosen, and not even uniquely so, when the wage is zero. A perturbation of this example can lead to one of the reverse substitution of labor. The switch point on the axis for the rate of zero would also become one at a positive wage. And that switch point might be the only switch point on the frontier at a non-negative rate of profits. Around that switch point, a higher wage is associated with cost-minimizing firms hiring more workers to produce a given gross output of corn. The labor coefficient in the corn-producing process for the technique preferred at a higher wage is larger.

Table 1: Coefficients of Production for The Technology

Input	Iron	Corn Industry
		Alpha	Beta
Labor	1	0.64097922	0.64097922
Iron	9/20	0.00157618	0.01686787
Corn	2	0.48125981	0.0674715

Table 1 specifies the technology in my usual way. I assume labor is advanced, and wages are paid out of the product at the end of a production cycle. I take a unit of corn as numeraire. Prices of production are here defined with a uniform rate of profits between the industry. I found this example with numerical exploration, so there is some round-off error in the figures.

This post is another demonstration that explaining wages and employment by supply and demand, even under ideal competitive conditions, is incoherent nonsense.

A Market Algorithm

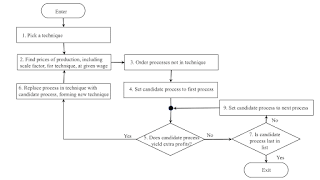
Figure 1: Specification of a Market Algorithm

1.0 Introduction

This article is heavily based on Bidard (2004).

An approach to the analysis of the choice of technique, in keeping with construction of the outer envelope of wage curves, is to consider replacing processes, more or less, one at a time. This post presents this approach as following an algorithm.

Assume that a set of techniques exist where all techniques are at least viable, indecomposable, and produce the same set of commodities. From the set of techniques, one can form a set of processes. In each process, workers produce a single commodity at the end of the year from certain inputs. The inputs, by assumption, are totally consumed in the course of the year. I also assume that the numeraire is specified.

Consider the algorithm specified by the flowchart in Figure 1. For this to be an algorithm, Steps 1 and 3 must be fully specified. One might as well assume that a known pseudo random number generator is used with a specified initial seed. Whether or not a candidate process yields extra profits is found in Step 5 with the prices of production calculated in Step 2. A process yields extra profits if and only if:

p a_.,j (1 + r) + w a_0,j > p_j

where a_0,j is the direct labor coefficient, and a_.,j is a column vector for the new process. I am imagining that a_.,j is the j column of the Leontief input-output matrix for a new technique. This new technique is formed by replacing a process in the technique previously selected in Step 2. Since, by assumption, no joint production exists, the process to be replaced is easily found. It is the process in the current technique that produces the same commodity as the candidate process. I have taken the wage as given in this specification of the algorithm. One could just as well take rates of profits as given.

This algorithm converges to a cost-minimizing technique. Consider the sequence of Steps enumerated as ‘2, 3, 4, (5, 7, 9)*, 5, 6, 2’. This expression denotes a single path around the loop on the bottom left of Figure 1, including zero or more paths around the loop on the right. As long as the loop on the right is repeated less times than the number of techniques, this path can be repeated. The question arises whether or not this algorithm contains an infinite loop. In a simple case, a process would be introduced into a technique because it is cost-minimizing for prices corresponding to the first technique, and that first technique would be cost-minimizing at the prices corresponding to the new technique. It can be shown that the existence of an infinite loop is impossible, under the assumption that no joint production exists. The algorithm always terminates.

(The use of metalinguistic symbols of parentheses and an asterisk to denote a repeated sequence of symbols is a convention in defining regular expressions. A sequence of symbols in a language, where the grammar of that language is specified by a regular expression, is accepted by a finite state machine, a type of automata. This is the lowest level of the Chomsky hierarchy. Chomsky (1965) uses transformational grammars to characterize human languages, which he argues are at the highest level of the hierarchy.)

Furthermore, except at switch points, the cost-minimizing technique found by the algorithm is unique. Which technique is initially selected at Step 1 or how processes are ordered at Step 3 does not matter, except for performance. The same cost-minimizing technique is ultimately found. The algorithm terminates with the selection of any one of the techniques that are cost minimizing at a switch point, depending on these details.

The algorithm is specified sequentially in Figure 1. Steps 3, 4, 5, 7, and 9 can be distributed. Inasmuch as this algorithm is executed in a capitalist economy, these steps are, in fact, distributed across firms. One might also modify the algorithm to apply when the set of processes and techniques are not known at that start of algorithm. Innovation and technical progress can be accommodated with an appropriate modification of Step 4 and Step 9. Step 7 should be eliminated, and the algorithm would be defined without a termination step, like daemons in operating systems. When the algorithm is modified for distributed processing, more than one process might be introduced into a technique simultaneously, including in the same industry. For which technique, then, are prices calculated in Step 2? This relates to the question of when labor expended in new processes is ‘socially necessary’, as Marx put it.

References

• Bidard, Christian. 2004. Prices, Reproduction, Scarcity. Cambridge: Cambridge University Press.
• Chomsky, Noam. 1965. Aspects of the Theory of Syntax. Cambridge: M.I.T. Press.