More On A Fixed Capital Example

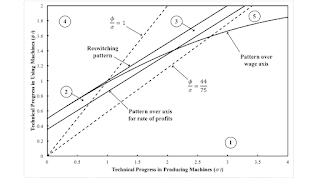
Figure 1: A Partition of a Parameter Space for the Schefold Example

1.0 Introduction

I want to revisit a perturbation analysis of an example, from Bertram Schefold, of reswitching with fixed capital.

Suppose workers use a machine to produce something or other, where the machine lasts several production periods. It is a possible choice to run the machine for less than its full physical life. One might think that choosing to adopt a technique with a longer economic life of the machine is, in some sense, more capital-intensive than choosing to junk it sooner. And this will lead to more output per worker. But, I am surprised to say, this is just not so. The underlying vision of Austrian-school economists is wrong even here.

If I worked through all the problems, with full understanding of their implications, in Kurz and Salvadori (1995), I would probably already know this. But, at least, I can make this point by examining perturbations of a single numeric example.

2. Technology

Table 1 shows the coefficients of production for the three processes comprising the available technology. Inputs must be available at the beginning of the year, and outputs become available at the harvest at the end. In the first process, labor uses inputs of corn to produce a new machine. That machine is used by labor in the second process, with inputs of seed corn, to produce more corn and a one-year old machine. In the third process, labor uses inputs of seed corn and the one-year old machine to produce corn. (I did think of calling the machine a "tractor".) The machine varies in physical efficiency over the course of its lifetime. In its second year, it requires less labor to tend it, but more inputs of corn.

Table 1: Coefficients of Production for The Technology

Input	Process
	(I)	(II)	(III)
Labor	(1/10) e1 - σ t	(43/40) e1 - φ t	e1 - φ t
Corn	(1/16) e1 - σ t	(1/16) e1 - φ t	(1/4) e1 - φ t
New Machines	0	1	0
Old Machines	0	0	1
Outputs
Corn	0	1	1
New Machines	1	0	0
Old Machines	0	1	0

I postulate the possibility of technical progress. The parameter σ specifies the rate of technical progress in producing machines, while φ specifies the rate of technical progress in using machines to produce corn. When (σ t) and (φ t) are unity, this is a reswitching example from Bertram Schefold (1980: 179). Corn is assumed to be the only consumer good, and it also is used as circulating capital. I also take a unit of corn as the numeraire.

A choice of technique arises. I call Alpha the technique in which the machine is operated only one year, and I assume free disposal. Beta is the technique in which the machine is operated for its full physical life time.

3.0 Price Equations

I take corn as numeraire. Although I do not make use of this generality in this post, I formulate systems of equalities and inequalities for prices of production with the possibility of persistent differences in the rate of profits among processes. p₁ is the price of a new machine, p₂ is the price of an old machine, w is the wage, and r is the scale factor for the rate of profits. The relative rates of profits are specified by given ratios s₁, s₂, and s₃ for the processes, which I take to be unity throughout. Coefficients of production are taken as given; one might think of the parameter t as expressing a very slow, secular time. With these parameters, and either the wage or the scale factor for the rate of profits taken as given, one solves for the prices of new and old machines, the other distributive variable, and the choice of technique.

3.1 Price Equations for the Alpha Technique

Suppose the Alpha technique is cost-minimizing, and the machine is discarded after being used for one year. The price of a new machine, the wage, and the scale factor for the rate of profits are related by the following two equations:

[(1/16) e^{1 - σ t}](1 + s₁ r) + [(1/10) e^{1 - σ t}] w = p₁

[(1/16) e^{1 - φ t} + p₁](1 + s₂ r) + [(43/40) e^{1 - φ t}] w = 1

The first equations comes from the process for producing a new machine. The second equation comes from the process for producing corn with a new machine. The price of an old machine is zero:

p₂ = 0

For the Alpha technique to be cost-minimizing, extra profits must not be available from operating the process that produces corn with an old machine. That is, the cost of a unit level operation of that process must not fall below revenues:

[(1/4) e^{1 - φ t}](1 + s₃ r) + [e^{1 - φ t}] w ≥ 1

A switch point exists when the above equation is met with equality.

3.2 Price Equations for the Beta Technique

Now suppose the Beta technique is cost-minimizing. The prices of a new and old machine, the wage, and the scale factor for the rate of profits are related by three equations:

[(1/16) e^{1 - σ t}](1 + s₁ r) + [(1/10) e^{1 - σ t}] w = p₁

[(1/16) e^{1 - φ t} + p₁](1 + s₂ r) + [(43/40) e^{1 - φ t}] w = 1 + p₂

[(1/4) e^{1 - φ t} + p₂](1 + s₃ r) + [e^{1 - φ t}] w = 1

For the Beta technique to be cost-minimizing, the price of an old machine must not be negative.

p₂ ≥ 0

Here, too, a switch point exists when the above equation is met with equality. Suppose prices of production for the Beta technique yield a negative price for an old machine. This is a signal to firms that they should truncate the economic life of the machine. They should only operate it for one year.

4.0 Perturbations

I do my usual thing of analyzing how the choice of technique varies with technical progress along a secular path, given values of parameters that specify the rate of decrease in specified coefficients of production. Technical progress in the example reduces the inputs of labor and circulating capital needed to produce a given output. The notation allows the rate of technical progress to differ between the machine and corn industries. The rate of technical progress is assumed to affect both processes that produce corn in the same way, whether or not the machine the workers use is new or old.

4.1 A Temporal Path

The choice of technique varies with distribution and technical progress. Figure 2 illustrates one particular ratio of the rate of technical progress in producing machines to the rate in using machines. Changes in the number and characteristics of switch points occur with patterns already described in previous blog posts. Switch points appear over the axis for the rate of profits and over the wage axis. Schefold's particular parameterization occurs just before switch points vanish in a reswitching pattern.

Figure 2: A Case of Variation in Switch Points with Technical Progress

4.2 Another Temporal Path

Figure 3 illustrates another particular ratio of the rate of technical progress in producing machines to the rate in using machines. Here too, the technical progress in using machines overwhelms technical progress in producing machines, and this is manifested by a transition ultimately from a region in which the economic life of a machine is one year to a region in which its economic life is its whole physical life, whatever the distribution of income. In this example of technical progress, a pattern over the wage axis precedes a pattern over the axis for the rate of profits. A reswitching example arises and disappears. It is then cost-minimizing to run the machine for its full physical life at high and low wages, but at intermediate wages cost-minimizing firms will truncate the economic life of the machine.

Figure 3: Another Case of Variation in Switch Points with Technical Progress

4.3 A Partition of the Parameter Space

At each point on the two paths through logical time characterized by Figures 2 and 3, the amount of technical progress in producing machines and in using machines is specified. Figure 1 partitions the resulting parameter space, based, as usual, on the number and characteristics of switch points in the choice of technique. Table 2 notes the switch points and lists the cost-minimizing technique, from a low to a high wage, for each numbered region. The locii separating Regions 1 and 2 and Regions 3 and 4 are parallel affine functions. The locus for the reswitching pattern is tangent to the locus for the pattern over the wage axis at the intersection of Regions 2, 3, and 4. Figure 1 demonstrates the applicability of the taxonomy of fluke switch points to the case of fixed capital.

Table 2: The Wage Frontier in Selected Regions in Parameter Space

Region	Switch Points	Cost-Minimizing Techniques
1	None	Alpha
2	One	Beta, Alpha
3	Two	Beta, Alpha, Beta
4	None	Beta
5	One	Alpha, Beta

The Schefold example is in narrow edge at the left of Region 3, along the dotted line corresponding to Figure 2. Just as this approach of partitioning (projections of) parameter spaces can be used to construct fluke switch points, it can also be used to improve examples of non-fluke switch points. Other parameters in Region 3 can result in switch points further apart on the wage frontier. The price of an old machine, at prices of production for the Beta technique, can be more noticeably negative when the Alpha technique is cost-minimizing.

5.0 Compare and Contrast Regions 2 and 5

Comparing and contrasting the single switch point in Regions 2 and 5 is interesting. Figures 4 and 5 illustrate the application of the direct method to analyze the choice of technique. When the machine is junked after one year, the price of an old machine is zero. Figure 4 shows extra profits in operating the machine for the second year with prices of production in this case. Around the switch point in Region 2, it pays to run the machine for a second year for higher rates of profits. On the other hand, around the switch point in Region 5, it pays to run the machine for the second year at lower rates of profits. Figure 5 shows the price of the old machine, given prices of production, when the machine is run for two years. A negative price shows that the cost-minimizing firm should truncate the economic life of machine to one year. Both figures yield the same conclusion about the choice of technique in the two regions. (This consistency is guaranteed in a pure fixed capital example with no superimposed joint production.)

Figure 4: Regions 2 and 5 with Price of Old Machine of Zero

Figure 5: Price of Production when Machine Runs for Two Years

Around the switch points in both Regions 2 and 5, a lower wage is associated with cost-minimizing firms wanting to hire more labor, given net output (Table 3). As one might expect, the adoption of a more labor-intensive technique is associated with lower net output per worker. It seems that the economic life of a machine cannot be mapped to the capital-intensity of a technique. Adopting a technique in which a machine is run longer is not necessarily more capital-intensive in that it does not necessarily raise output per worker for the economy as a whole. This counter-intuitive result, at least by traditional neoclassical and Austrian teaching, obtains in Region 2.

Table 3: Selected Characteristics of Switch Point in Regions 2 and 5

	Region 2	Region 5
Economic Life of Machine	Run for two years at higher rate of profits	Run for one year at higher rate of profits
Consumption per Person-Year	Decreased at higher rates of profits	Decreased at higher rate of profits
Employment, given net corn output	Increased at lower wage	Increased at lower wage

6.0 Conclusion

Unambiguous physical measures are available here for examining central claims in Austrian capital theory. Net output in a stationary state in this model consists of a single consumption good, and labor is taken as homogeneous. Around a switch point exhibiting capital-reversing, a lower interest rate is associated with the adoption of a technique that produces less net output per unit of labor time. If a financial measure of capital intensity is adopted such that, around all switch points, lower interest rates are associated with the use of a technique with a longer average period of production, the association between more roundabout methods of production and greater productivity is broken. Austrian capital theory and Austrian business cycle theory fails to be sustained

In a model of fixed capital with only a single machine in use, the number of production cycles for the economic life of the machine is an unambiguous measure of roundaboutness. The numerical example in this chapter reveal that no connection necessarily exists between lower interest rates and the extension of the economic life of a machine. The example in Region 3 is a reswitching example. Necessarily, in a reswitching example in a model of fixed capital, a lower rate of profits is associated, around one of the switch points, with the truncation of the economic life of the machine.

The Austrian theory of capital is also refuted in Region 2 in the example, even with a single switch point. Around the switch point, a lower rate of profits is associated with a truncation of the economic life of a machine, not the extension of how long this machine is used in production cycles. And that truncation is associated with a more capital-intensive technique, as is seen in an increase in net output per worker. These examples demonstrate that the underlying vision behind the Austrian story is simply incorrect. Attempts to evade this proof by adopting a financial definition of capital simply ignore the points at issue.

Financial Economics

This is a list of some of what I think one should know if one wants to talk to investors interested in theory. This post is not about making money and is probably not up-to-date. My references are fairly popular, and mostly old. I include one recent popular book as an example. Most of the references I do not recall very well, and I have not read Ben Graham. But many seem to know that Warren Buffet recommends this book. This post is non-critical. Keen and Quiggin in Debunking Economics and Zombie Economics, each have a chapter of criticism.

• Behavioral finance: The application of behavioral economics to finance.
• Beta: A parameter in the CAPM.
• Black Scholes formula: A formula for pricing options.
• Capital Asset Pricing Model (CAPM): A model that relates the risk of an asset to the market as a whole.
• Efficient Market Hypothesis (EMH): A model in which all information is quickly built into asset prices. The EMH comes in at least three types.
• Equity Premium Puzzle: The observed phenomena for stocks (or shares) to trade at higher prices, as compared to bonds, than can be justified by the EMH.
• Lévy distribution: A family of probability distributions that, except for the limiting case of the Gaussian distribution, have an infinite variance. The Cauchy distribution is also a member. Benoit Mandelbrot recommends this as a model for changes in asset prices.
• Martingale Theory: A branch of mathematics in which a stochastic process exhibits a special case of the Markov property. I recall learning about a drunkards walk and the gambler's ruin problem, but I do not recall this term in any of my formal math courses.
• Modigliani and Miller (M and M): A model that implies, under idealizations, that it does not matter if corporations finance investments with equity or debt.
• Noise trading: Trading on random variations in the price of an asset, instead of fundamentals. I know of this from some late 80s work of DeLong, Shleifer, Summers, and Waldmann.
• Stochastic Calculus, also known as Ito Calculus: A branch of mathematics in which one can talk about the derivatives and integrals of a set of random variables indexed on continuous time. Such a stochastic process is different from a single realization).
• Value-at-risk: A formula that applies to an investment portfolio.
• Volatility skew: An anomaly, inconsistent with the Black-Scholes formula, that emerged in markets for options.

One also needs to know about puts, calls, indices, credit default swaps, types of spreads (e.g. a broken wing butterfly spread) and so on if one wants to be a financial analyst. As usual, this is an aspirational post. I do not claim to know all of this, and maybe I have gotten some of the above incorrect.

References

• Akerlof, George A. and Robert J. J. Shiller. 2010. Animal Spirits: How Human Psychology Drives the Economy, and Why It Matters for Global Capitalism. Princeton University Press.
• Bernstein, Peter L. 2009. Capital Ideas: The Improbable Origins of Modern Wall Street.
• Davies, Daniel. 2018. Lying for Money: How Legendary Frauds Reveal the Workings of our World. Profile Books.
• Derman, Emanuel. 2016. My Life as a Quant: Reflections on Physics and Finance.
• Graham, Benjamin. The Intelligent Investor
• Henwood, Doug. 1997. Wall Street: How It Works and for Whom. Verso.
• MacKenzie, Donald. 2008. An Engine, Not a Camera: How Financial Models Shape Markets. MIT Press.
• McCauley, Joseph L. 2009. Dynamics of Markets: The New Financial Economics, 2nd edition. Cambridge University Press.
• Thorp, Edward O. and Sheen T. Kassouf. 1967. Beat the Market: A Scientific Stock Market System.

Elsewhere

• A podcast interview with Philip Mirowski about how, roughly, neoliberals are exploiting the Corona Virus crisis in America.
• A book, Nine Lives of Neoliberalism, edited by Dieter Plehwe, Quinn Slobodian, and Philip Mirowski. Somewhere this is or was freely downloadable in PDF.
• A podcast interview with Marshall Steinbaum about the Chicago school of economics.
• A podcast episode, by two economics professor, trying to present an overview of Joan Robinson.
• A downloadable book, Labour and Value: Rethinking Marx's Theory of Exploitation, by Ernesto Screpanti.
• Two young friends discuss Steve Keen's book, Debunking Economics.

A Refutation Of Austrian Capital Theory And Austrian Business Cycle Theory

1.0 Introduction

I have not posted about a non-fluke switch point in a while. This is an example from Bertram Schefold. I have examined perturbations and variations of this example before.

Here I present an example with tables exhibiting arithmetic. Is this any more transparent than examples presented with graphs?

I have been listening to some lectures on YouTube, especially Richard Wolff. I now have another hypothesis why mainstream economists have been promoting lies, ignorance, and nonsense for half a century: fear. The history of economics includes purge after purge after purge. Maybe many mainstream economists are cowed by their rulers.

2.0 Technology

Three processes are available for use in production. Each process is specified by coefficients of production (Table 1), when operated at an unit level. The person-years of labor employed, the bushels of corn used up in a process, and the number of new and old machines are specified. Outputs consist of bushels corn and new and old machines. Corn is both a consumer good and functions as circulating capital. Machines function as fixed capital. A machine's productivity varies with its age. An older machine requires less labor to operate, but more circulating capital.

Table 1: Coefficients of Production for The Technology

Input	Process
	(I)	(II)	(III)
Labor	1/10	43/40	1
Corn	1/16	1/16	1/4
New Machines	0	1	0
Old Machines	0	0	1
Outputs
Corn	0	1	1
New Machines	1	0	0
Old Machines	0	1	0

Suppose all three processes are run at unit level in parallel. At suppose at the start of the year, the firm has one new machine, one one-year old machine, and 3/8 bushels corn. The output of the first process is one new machine. The previously existing new machine is consumed in the second process, leaving an output of one one-year old machine. The third process uses up the one one-old year machine. So these processes reproduce the stock of new and old machines. But they also use up inputs of 3/8 bushels corn in producing a gross output of two bushels corn. Summing over all three processes, 2 7/40 person years of labor produce, with the capital stock, a net output of 1 5/8 bushels corn. The labor intensity of this technique is 87/65 person-years per bushel.

Assume free disposal for old machines. Another technique would be operated when the use of the machine is truncated after one year. In this case, one should consider the first and second processes being run in parallel at unit level, with a capital stock of one new machine and 1/8 bushels corn reproduced each year. Under this technique, 1 7/40 person years of labor are employed across the two processes. Net output is 7/8 bushels corn. The labor intensity is 47/35 person-years per bushel.

The more labor-intensive technique is the one with the truncated economic life of the machine. How many production cycles firms choose to run machines is an unambiguous physical measure in this example. And choosing to run the machine longer is a choice to adopt a less labor-intensive technique. Just as Eugen Böhm Bawerk says, a longer period of production, in some sense, is a more capital-intensive method. And that increase in the period of production results in greater output per worker. (I am not claiming that the number of production processes is the Austrian average period of production. I am merely noting how transparent the use of time is in this example.)

3.0 Some Accounting

One can easily see how a single firm would operate the last two processes in parallel, or only the process using the new machine, if the use of the machine is truncated. If such a firm was vertically integrated, they would also produce new machines with the first process. The firm can take the wage and the price of corn from the market, under various idealizations. For simplicity, I take a bushel corn as the numeraire. What prices would the accountants use to evaluate new and old machines?

3.1 At an Initial Wage

Consider a starting wage of 35/71 bushels per person-year and prices of machines shown in Table 2. For each process, the cost of capital inputs are the sum of the inputs of corn and machines of specified vintages, evaluated at the given prices. Wages are found from the labor input, evaluated at the given wage. Revenues are the sum of the outputs of corn and machines of specified vintages, evaluated at given prices. I assume wages are paid at the end of the year. So the rate of profits is the ratio of the difference between revenues and wages to the capital costs. With these prices, the owners are happy to operate all three processes. They make the same rate of processes in each, and prices do not signal that they should make any changes.

Table 2: Initial Prices

w = 35/71 ≈ 0.4930, p0 = 99/568 ≈ 0.1743, p1 = 1/284 ≈ 0.003521
	Capital Costs	Wages	Revenues	Rate of Profits
I	0.0625	0.04930	0.1743	100 percent
II	0.2368	0.5299	1.004	100 percent
III	0.2535	0.4930	1	100 percent

3.2 A Higher Wage

Now suppose the wage is 9,055/14,016 bushels per person-year. Table 3 shows accounting when the prices of new and old machines are unchanged. Notice that the rate of profits has fallen, with the rise in the wage, in all processes. But it has fallen to different levels, given that ratio of wages to the cost of capital originally varied among the processes. David Ricardo discusses this effect in the first chapter of his Principles of Political Economy and Taxation. Obviously, the price at which machines are entered into the firm's books must be changed to reflect the change in wages.

Table 3: Initial Prices with Raised Wage

w = 9,055/14,016 ≈ 0.6460, p0 ≈ 0.1743, p1 ≈ 0.003521
	Capital Costs	Wages	Revenues	Rate of Profits
I	0.0625	0.06460	0.1743	75.5 percent
II	0.2368	0.6945	1.004	30.5 percent
III	0.2535	0.6460	1	39.6 percent

Table 4 shows a set of prices such that the same rate of profits is obtained in all three processes. This is not the end of the story, though, The price of a one-year old machine is slightly negative. (My approach for perturbing reswitching examples can make this price more noticeably negative, but maybe I would end up with even more messy fractions.) Instead of decreasing the revenues for the second process from the output of old machines, the managers of the firm can simply throw the old machine away and enter a price of zero for it on its books.

Table 4: Raised Wage and Updated Prices of New and Old Machines

w = 9,055/14,016 ≈ 0.6460, p0 ≈ 0.1531, p1 ≈ -9.563 x 10-5
	Capital Costs	Wages	Revenues	Rate of Profits
I	0.0625	0.06460	0.08852	41.64 percent
II	0.2156	0.6945	0.3054	41.64 percent
III	0.2499	0.6460	0.3539	41.64 percent

Table 5 shows the result of truncating the use of machines. One must, however, set a new accounting price for new machines, as well. Without this adjustment, different rates of profits are obtained in the first two processes. Notice the rate of profits is indeed lower in the third process, which is not used by cost-minimizing firms.

Table 5: Raised Wage and Truncated Use of Machines

w = 9,055/14,016 ≈ 0.6460, p0 ≈ 0.15313, p1 = 0
	Capital Costs	Wages	Revenues	Rate of Profits
I	0.0625	0.06460	0.15313	41.64 percent
II	0.21563	0.6945	1	41.68 percent
III	0.25	0.6460	1	41.58 percent

Table 6 shows the final results of correct accounting, with increased wages. The rate of profits, r, is 5/12, halfway between 1/3 and 1/2. Those rates of profits are the switch points in this example. I have told this story as a matter of accounting for vertically integrated firms. But these are the only prices on the market consistent with a long period position with the postulated wage. How and whether market prices would converge to these prices of production, in a gravitational process (as in Adam Smith's metaphor) is not clear to me. I like the idea that Sraffa's book is about little more than accounting. This idea is not too far away from what Ajit Sinha has been arguing for a number of years.

Table 6: Raised Wage, Truncation, Updated Price of New Machines

w = 9,055/14,016 ≈ 0.6460, p0 = 1,431/9,344 ≈ 0.15315, p1 = 0
	Capital Costs	Wages	Revenues	Rate of Profits
I	0.0625	0.0646	0.15315	41.67 percent
II	0.21565	0.6945	1	41.67 percent
III	0.25	0.6460	1	41.58 percent

3.3 Summary

Table 7: Summary

Wage	Labor Intensity	Rate of Profits
35/71 ≈ 0.4930 bushels per person-yr.	87/65 ≈ 1.338 person-yrs. per bushel	100 percent
9,055/14,016 ≈ 0.6460 bushels per person-yr.	47/35 ≈ 1.343 person-yrs. per bushel	5/12 ≈ 41.7 percent

At a higher wage, firms want to run machines for one year, not two years. The economic life of machines is shortened from the physical life. And firms want to hire more workers to produce a net output.

Why might the wage rise and the rate of profits fall? In one theory, known to be nonsense, a shock might lead to labor be less abundant, as compared to capital. Perhaps people become more forward-looking and more willing to save, or the population falls for some reason. Wages rise, and firms take this as a signal to substitute capital for labor. But, in the example, a higher wage is associated with the adoption of a less capital-intensive technique and a rise in labor intensity. Somehow, if equilibrium is to be obtained, an increase in the labor force must be accompanied by a rise in wages.

Perhaps one can find a financial measure of capital, such as Hicks' average period of production, where a higher capital-intensity is always associated with a lower rate of profits around a switch point. But then one would have to grapple with the fact that more 'capital' does not always result in more output. Austrian school economists cannot seem to handle that their theory of 'malinvestment' is just incorrect.