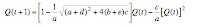Which Side Are You On, Bob?

"My impression is that the best and brightest in the profession proceed as if economics is the physics of society. There is a single universally valid model of the world. It only needs to be applied. You could drop a modern economist from a time machine - a helicopter, maybe, like the one that drops the money - at any time, in any place, along with his or her personal computer; he or she could set up in business without even bothering to ask what time and which place. In a little while, the up-to-date economist will have maximized a familiar-looking present-value integral, made a few familiar log-linear approximations, and run the obligatory familiar regression. The familiar coefficients will be poorly determined, but about one-twentieth of them will be significant at the 5 percent level, and the other nineteen do not have to be published. With a little judicious selection here and there, it will turn out that the data are just barely consistent with your thesis advisor's hypothesis that money is neutral (or nonneutral, take your choice) everywhere and always, modulo an information asymmetry, any old information asymmetry, don't worry, you'll think of one." -- Robert M. Solow (1985). "Economic History and Economics", American Economic Review, V. 75, N. 2 (May): 328-331

Paul Davidson, Overoptimistic

"The best way to evaluate any economic theory is to consider the theorist as a magician. Theorists rarely make logical errors in moving from axioms to conclusions, any more than professional prestidigitators drop the deck of cards while performing a card trick. Today's economic theorists are proficient at creating the illusion of pulling policy conclusion rabbits out of their black hat mathematical model of the economy. The more surprising the policy rabbits pulled from the hat, the greater the audience enjoyment of the economist's performance, and the greater the applause and rewards." -- Paul Davidson (2007). John Maynard Keynes, Palgrave Macmillan, p. 26.

This book should be added to your reading list if you are interested in Keynes' General Theory and are not informed of Davidson's views on Keynes. I wish Davidson had chosen a title that distinguishes his book from Hyman Minsky's of the same name.

Some Capital-Theoretic Fallacies of Austrian Economics

I have rewritten my demonstration of some errors in Austrian business cycle theory. In addition to making this article available on the Social Science Research Network, I have submitted it to some journal.

Invisible Hands Ere Adam Dug

I don't know that these usages have anything to do with Adam Smith. I don't even vouch for the translation from the seventeenth century french:

"How are you to get at a person who talks in this way, father? On what quarter will you assail me, since neither my words nor my writing afford the slighest handle to your accusations, and the obscurity in which my person is enveloped forms my protection against your threatenings? You feel yourselves smitten by an invisible hand - a hand, however, which makes your delinquencies visible to all the earth; and in vain do you endeavor to attack me in the person of those with whom you suppose me to be associated." -- Blaise Pascal, Provincal Letters, Letter XVII

"Be innocent of the knowledge, dearest chuck,
Till thou applaud the deed. Come, seeling night,
Scarf up the tender eye of pitiful day;
And with thy bloody and invisible hand
Cancel and tear to pieces that great bond
Which keeps me pale! Light thickens; and the crow
Makes wing to the rooky wood;
Good things of day begin to droop and drowse;
While night's black agents to their preys do rouse.
Thou marvell'st at my words: but hold thee still;
Things bad begun make strong themselves by ill.
So, prithee, go with me." -- William Shakespeare, Macbeth, Act 3, Scene 2

Liberal Anti-Marxism Annoying

Apparently young American liberals still feel obligated to take ignorant cold war stands. Here's Ezra Klein, in a post positioning himself as more reasonable than either extreme:

"Any Marxist will tell you that 'real' Marxism was never tried. That said, just about every time something called Marxism was tried, it traveled down much the same course, and failed in much the same way. "

Perhaps, I'm not the one to comment, since I neither consider myself to be a Marxist nor do I disagree with Klein's take on American conservatives.

It is simply untrue that "every time something called 'Marxism' was tried", it failed. Eduard Bernstein was called a Marxist "revisionist" - this was not a compliment by the communists. Bernstein's argument was important in the development of the Second International's line. And this version of Marxism is still being implemented in western Europe.

I also wonder what it means to "try" Marxism. The last of Marx's theses on Feuerbach is, famously:

"The philosophers have only interpreted the world differently, the point is, to change it."

The world still needs transforming. One finds few formulae in Marx, however, for what to do after the revolution*. Marx's longest work is more about analysis of existing society than unfounded designs of some far-distant future society. In the afterword to the second German edition, Marx notes that in Capital he is not "writing recipes (Comtist ones?) for the cookshops of the future." Perhaps some of Marx's analysis is still worth retaining.

Here's one part of Marx's analysis to consider:

"The general conclusion at which I arrived and which, once reached, became the guiding principle of my studies can be summarized as follows. In the social production of their existence, men inevitably enter into definite relations, which are independent of their will, namely relations of production appropriate to a given stage in the development of their material forces of production. The totality of these relations of production constitutes the economic structure of society, the real foundation, on which arises a legal and political superstructure and to which correspond definite forms of social consciousness. The mode of production of material life conditions the general process of social, political and intellectual life. It is not the consciousness of men that determines their existence, but their social existence that determines their consciousness. At a certain stage of development, the material productive forces of society come into conflict with the existing relations of production or - this merely expresses the same thing in legal terms - with the property relations within the framework of which they have operated hitherto. From forms of development of the productive forces these relations turn into fetters. Then begins an era of social revolution. The changes in the economic foundation lead sooner or later to the transformation of the whole immense superstructure." -- Karl Marx, Preface to A Contribution to the Critique of Political Economy

I do not see how the horrors of Stalinism or the 1989 collapse of "actually existing socialism" can invalidate the above general conclusion. In fact, that collapse would rather seem to illustrate Marx's conclusion.

* Caveat: Marx is probably most explicit on the design of post-revolutionary society in The Civil War in France and in the Critique of the Gotha Programme. It is in the latter, that Marx's makes his distinction between post-revolutionary socialism, in which laborers receive their proceeds in proportion to their contribution, and "the higher phase of communist society", in which

"society [can] inscribe on its banners: 'From each according to his ability, to each according to his needs!'".

Lenin draws on this distinction in his State and Revolution and in his attacks on the "renegade" Kautsky.

Vocabulary Word: Mumpsimus

Joan Robinson had lots to say about the Cambridge Capital Controversy. I find this remark to be amusing:

"I was delighted to find in a dictionary the word mumpsimus, which means stubborn persistence in an error that has been exposed" -- Joan Robinson

Laissez-Faire "Never Based On Solid Empirical And Theoretical Foundations"

"Friedman and the other shock therapists were also guilty of oversimplification, basing their belief in the perfection of market economies on models that assumed perfect information, perfect competition, perfect risk markets. Indeed, the case against these policies is even stronger... They were never based on solid empirical and theoretical foundations, and even as many of these policies were being pushed, academic economists were explaining the limitations of markets — for instance, whenever information is imperfect, which is to say always." -- Joseph Stiglitz, "Bleakonomics", New York Times, 30 September 2007

I've quoted Saari and Samuelson each saying the same.

Tyler Cowen: Slave To The Rhythm Of Power

Tyler Cowen purports to analyze why the pay of CEOs has increased so much.

"It is useless to ask what is the source of natural inequality, because that question is answered by the simple definition of the word. Again, it is still more useless to inquire whether there is any essential connection between the two inequalities; for this would be only asking, in other words, whether those who command are necessarily better than those who obey, and if strength of body or of mind, wisdom or virtue are always found in particular individuals, in proportion to their power or wealth: a question fit perhaps to be discussed by slaves in the hearing of their masters, but highly unbecoming to reasonable and free men in search of the truth." -- Jean Jacques Rousseau, A Dissertation on the Origin and Foundation of the Inequality of Mankind (Trans. by G. D. H. Cole)

Of course, CEOs cannot receive their pay except through services provided to them by a society existing beforehand:

"The difference of natural talents in different men is, in reality, much less than we are aware of; and the very different genius which appears to distinguish men of different professions, when grown up to maturity, is not upon many occasions so much the cause, as the effect of the division of labour. The difference between the most dissimilar characters, between a philosopher and a common street porter, for example, seems to arise not so much from nature, as from habit, custom, and education. When they came into the world, and for the first six or eight years of their existence, they were, perhaps, very much alike, and neither their parents nor playfellows could perceive any remarkable difference. About that age, or soon after, they come to be employed in very different occupations. The difference of talents comes then to be taken notice of, and widens by degrees, till at last the vanity of the philosopher is willing to acknowledge scarce any resemblance. But without the disposition to truck, barter, and exchange, every man must have procured to himself every necessary and conveniency of life which he wanted. All must have had the same duties to perform, and the same work to do, and there could have been no such difference of employment as could alone give occasion to any great difference of talents.

As it is this disposition which forms that difference of talents, so remarkable among men of different professions, so it is this same disposition which renders that difference useful. Many tribes of animals acknowledged to be all of the same species, derive from nature a much more remarkable distinction of genious, than what, antecedent to custom and education, appears to take place among men. By nature a philosopher is not in genius and disposition half so different from a porter, as a mastiff is from a greyhound, or a greyhound from a spaniel, or this last from a shepherd's dog." -- Adam Smith, Wealth of Nations

General Equilibrium: Same As It Ever Was

Some mainstream economists (e.g., Bliss and Hahn) responded to the Cambridge Capital Controversy by taking their stand on the Arrow-Debreu very short run model of intertemporal General Equilibrium. They claimed that this model is logically consistent, and it is unaffected by Sraffa effects. I think the latter proposition, at least, is debatable.

Be that as it may, perhaps the Sonnenschein-Mantel-Debreu results show that the Arrow-Debreu model has no empirical implications. That is, the theory imposes no restrictions on the directions of aggregate movements in prices and quantities in response to changes in the data. Kenneth Arrow, Alan Kirman, D. Saari, and S. Abu Turab Rizvi are some who have advanced this claim.

Some have challenged my understanding on this claim, pointing out some work done by Donald Brown and others. S. Abu Turab Rizvi has recently reviewed this recent work ("The Sonnenschein-Mantel-Debreu Results after Thirty Years", History of Political Economy, V. 38 (Annual Supplement): 228-245). He concludes that:

"...Brown and Matzkin do provide a restriction that can conceivably be refuted... Despite this ..., if the only data ... are at the aggregate level, general equilibrium theory does not generate refutable restrictions... [T]he Brown-Matzkin results require individual-level ... vectors.

Matters are even clearer on qualitative features ... such as local uniqueness, stability, and comparative statics. The equilibrium manifold approach ... does not allow us to refute statements on these features... [W]e cannot test to see if an economy is poorly behaved... [T]he intuition that general equilibrium theory is devoid of meaningfully general results remain true..."

I continue to remain puzzled about what mainstream economists take the content of price theory to be.

Facts Are Getting The Best Of Them

Paul's done this sort of amusing thing before:

"Now as they survey the wreckage of their cause, conservatives may ask themselves: 'Well, how did we get here?' They may tell themselves: 'This is not my beautiful Right.' They may ask theselves" 'My God, what have we done?'" -- Paul Krugman (2007). "Same Old Party", New York Times (8 Oct): A19

Heterodoxy Again And Other Links

• Inside Higher Ed has an article about heterodox economics. Some of those quoted and others have commented.
• A blogger is hosting a reading group for Keynes' General Theory
• I've thought Matt Yglesias could not accept that his Econ 10 teacher at Harvard is a propagandist, not a scholar. (I'm aware that Matt Y.'s study involved quite a bit of philosophy.) So I am amused to read him writing:

"Have I ever mentioned that philosophers tend to think that economics is vacuous? Which isn't to say that you shouldn't listen to economists. These days, they tend to know a lot of math, and math is a very useful thing."

• Update (8 Oct):Scientific American has a short article in the July 2007 issue on neuronomics and the empirical falsity of economic man.
• This post on Post Autistic Economics is interesting for the comment from Bertil, a "French PhD candidate in economics"
• The Colander, Holt, and Rosser paper, "Live and Dead Issues in the Methodology of Economics" comments on how they see the different distinctions between mainstream and nonmainstream and orthodox and heterodox economics

One, Two, Three, Many Economics?

Marc Lavoie's article "Do Heterodox Theories Have Anything in Common? A Post-Keynesian Point of View" (Intervention, V. 3, N. 1 (2006): 87-112) is a contribution to an ongoing discussion. The first paragraph of this article mentions "Marxist economists, Sraffians..., structuralists..., institutionalists, regulationists, social or humanist economists, anti-utilitarists, behaviorists, economists of conventions, Schumpeterians (or evolutionary economists), circuitists, and feminist economists." But the focus seems to be on Post-Keynesians and the supposed split between fundamentalist Keynesians, Kaleckians, and Sraffians.

The label of fundamentalism as a type of Keynesians goes back at least to Alan Coddington. Keynesians of this type emphasize Chapter 12 of The General Theory and decision-making under radical uncertainty. Exemplars include Joan Robinson and Paul Davidson. One useful contrast is with "hydraulic" or "bastard Keynesians", such as exemplified by J. R. Hicks' IS/LM model under mainstream interpretations.

The perception of splits within Post Keynesianism also goes back to the late 1970s or early 1980s, with, for example, arguments between Joan Robinson and Pierangelo Garegnani. Robinson argued that Sraffianism, as a constructive theory for analyzing economies de-emphasized uncertainty too much, with its emphases on a long-period method. Garegnani has argued something like an emphasis on fundamental uncertainty cedes too much to the neo-classical (or mainstream) belief that labor markets tend to clear in the long-run and that Keynes offered a theory only applicable to the short-run. Paul Davidson extends and embraces Robinson's view that Sraffians cannot be part of an useful Post Keynesianism. Followers of Kalecki have gone their own way. At one point, Steedman, however, attacked some followers of Kalecki for missing the influence of distribution on relative prices. This influence needs to be accounted for in Kalecki's markup pricing. Harcourt has written of a "hourses for courses" approach and questioned whether Post Keynesianism could or should be one school of thought.

I think the Joan Robinson viewpoint is not too relevant to my usage of Sraffa's book as an internal critique of neoclassical theory. It is relevant if one tries to extend Sraffa to understand actual economies.

Lavoie finds some unifying elements in the views of Post Keynesians and others on rationality, price theory, growth theory, and the relationship between real and monetary analyses.

Invasion of the Name Snatchers: Supply-Side Economics

I steal half the title from James Galbraith. Italy is a foreign country, and, besides, Paolo Sylos Labini is dead:

"At the beginning of the sixties some issues that were to become the themes of supply-side economics were passionately discussed by a few Italian economists: Saraceno, Sylos Labini, Fuà, Caffè, Napoleoni and myself. The Italian economy was clearly incapable of assuring adequate growth of the various sectors and of all regions. There were sectors (such as agriculture) lagging behind, whereas the take-off of some regions (the South in particular) was hampered by structural conditions and chronic ineffiencies characterised other sectors (in Fuà's and Sylos' contributions attention was brought to the tertiary sector). It was our condition that an active economic policy, aiming at producing some specific structural changes, could help growth, facilitate the take-off in the South and reduce the divergence between the growth of private consumption and the expansion of social services. Such a conviction had some important implications for economic theory. It offered stimuli and arguments to go beyond the demand approach of both Keynesian and monetarist economists. The supply-side theories developed in the United States have perceived such a need only in a partial and distorted way, essentially by concentrating on fiscal problems. In the sixties we were convinced instead that to overcome the limitations of the demand approach - institutionalised in current macroeconomic theories - a coherent general strategy of economic policy should be devised such that conditions accounting for the efficiency of the whole system could be positively changed. Such a general strategy can be labelled as (indicative) planning. Planning is not to be conceived as an alternative to the market. Indicative planning can make market more efficient; in its turn, the efficiency of the private economy allows for more advanced goals to be pursued by planning.

The events of the sixties and seventies appear to have invalidated our view on the need for indicative planning..." -- Siro Lombardini (1993). "Foreword", in Market and Institutions in Economic Development: Essays in Honour of Paolo Sylos Labini (edited by Salvatore Biasco, Alessandro Roncaglia, and Michele Salvati), St. Martin's Press

Re-reading the above, I see that Lombardini doesn't say that this group of economists actually used the label "supply-side economics".

Chaotic Cobwebs (Part 1 1/2)

5.0 Return to a Special Case

This post continues the examination of a cobweb cycle with a non-linear demand curve. In this part, I talk again about the special case examined in Section 3 of that previous post. In that case, the parameters b and e of the model are zero. Furthermore, I continue to assume c is 3/5 and d is 21/20. Figure 6 shows attracting limiting behavior for a whole range of the parameter a. The abscissa in this graph is a, with a set to unity at the right edge. The ordinate is the limiting values of the normalized quantity, Q(t). As I point out towards the right, a two-period cycle shows up on the graph as a plot of two values of the ordinate for the value of a for which that cycle is generated. One can see the period-doubling scenario leading to chaos as one moves to the left on the graph. By the way, this figure is a fractal, repeating on an infinite number of scales. It has both qualitative and quantitative universal features for a certain family of one-dimensional maps (for example, characterized by the Feigenbaum constant).

Figure 6: Structural Dynamics of a Special Case

6.0 An Economically Relevant Special Case

The case above has both demand and supply functions through the origin in the quantity-price space. I want to consider a case in which the demand curves intersects the price axis at a strictly positive price and slopes downward in the first quadrant. Accordingly, consider the case where a is unity, b is 781/960, c is 3/5, d is 1/2, and e is zero. (I put aside questions of whether adaptive expectations make sense here or whether a partial equilibrium framework with monotonic supply and demand curves is justified - see implications of the Sonnenschein-Debreu-Mantel theorem.)

Figure 7 shows how the price and quantity evolve for selected initial values. The red line suggests the point equilibriating of supply and demand is unstable. It will never be observed in this model. Instead, the red line evolves to a two-period limit cycle. The blue line shows that points outside that cycle will evolve inward to that cycle. As a matter of fact, I chose parameter values such that Figures 2 and 3 in Section 3 of the previous post show the behavior of the normalized quantity for this case.

Figure 7: Temporal Dynamics with All Positive Prices and Quantities

I don't see that one can find positive parameters values such that period doubling can lead to chaos in this model with price and quantity remaining positive throughout. Although I am not sure of this, I am willing to accept that the maximum of the quadratic function in Equation 4 (see previous post) must be strictly positive for chaos to arise in the first quadrant. I don't understand what Richard Goodwin graphs in Figures 2.4 and 2.5 of his book. Perhaps he is considering a cubic demand curve or some other higher polynomials for supply and demand.

Update (28 Sep.): A Google search on "cobweb", "chaos", and "economics" shows lots of literature, mostly behind paywalls. I notice particularly work by Barkley Rosser, Jr. and in the Journal of Economic Behavior and Organization, which he edits. So I have reading I could do.

Writing Down Von Neumann's Contributions to Game Theory

Today's New York Times, in the science section, contains an ad for the "Von Neumann Memorial Lectures". This reminded me that, several years ago in the Times, Hal Varian misrepresented Von Neumann's treatment of game theory:

"Modern game theory was developed by the great mathematician John Von Neumann in the mid-1940s. His goal was to understand the general logic of strategic interaction, from military battles to price wars.

Von Neumann, working with the economist Oscar Morgenstern, established a general way to represent games mathematically and offered a systematic treatment of games in which the players' interests were diametrically opposed. Games of this sort - zero-sum games - are common in sporting events and parlor games.

But most games of interest to economists are non-zero sum. When one person engages in voluntary trade with another, both are typically made better off. Although von Neumann and Morgenstern tried to analyze games of this sort, their analysis was not as satisfactory as that of zero-sum games. Furthermore, the tools they used to analyze these two classes of games were completely different.

Mr. Nash came up with a much better way to look at non-zero-sum games. His method also had the advantage that it was equivalent to the von Neumann-Morgenstern analysis if the game happened to be zero sum." -- Hal R. Varian (2002).

I find it hard to read this as saying anything other than:

• Nash generalized the Von Neumann and Morgenstern (VNM) solution to zero-sum games to a solution (the Nash solution) applying to both zero-sum and non-zero-sum games.
• Although VNM had a solution for non-zero-sum games, it was not a generalization of their solution for zero-sum games.

Both claims are false.

Varian's statement only makes sense if one pretends The Theory of Games and Economic Behavior (TGEB) is missing the almost 300 pages on zero-sum n-person games. Under this pretense, the only zero-sum games treated in TGEB would be two-person games. The Nash equilibrium is, in some sense, a generalization of the VNM minimax treatment of two-person zero sum games. And the TGEB treatment of coalitions in non-zero sum games is something else.

VMN do decompose their treatment of games into two phases, but not based on whether or not a game is zero sum. They decompose their treatment into zero-sum two-person games and all other games (All quotations of numbered paragraphs are of the third edition of TGEB):

"66.1.2. Our theory of games divides clearly into two distinct phases: The first one comprising the treatment of the zero-sum two-person game and leading to the definition of its value, the second one dealing with the zero-sum n-person game, based on the characteristic function, as defined with the help of the values of the two-person games."

The TGEB solution of n-person zero-sum games is, in some sense, a generalization of the TGEB minimax solution of zero-sum two person games. One can form two "collective persons" for the n-person game, where each "person" is one of two coalitions:

"25.1.2. Suppose then that we have a game Gamma of n players... Without yet making any predictions or assumptions about the course a play of this game is likely to take, we observe this: if we group the players into two parties, and treat each party as an absolute coalition - i.e. if we assume full cooperation within each party - then a zero-sum two-person game results..."

In the TGEB treatment, a coalition can pool their winnings and then redistribute them to the players in the coalition. VMN define a solution to a game as a set of imputations of payouts to the players. The definition of the set of imputations is concerned with why a player would chose to be in one coalition or the other, and why the remaining members of the winning coalition would chose to woo a player or not.

To help fix intuition, VMN define an interesting zero-sum three person game, the Majority Game:

"21.1...Each player, by a personal move, chooses the number of one of the two other players. Each one makes his choice uninformed about the choices of the two other players.

After this the payments will be made as follows: if two players have chosen each other's numbers we say that they form a couple. Clearly there will be precisely one couple, or none at all. If there is precisely one couple, then the two players who belong to it get one-half unit each, while the third (excluded) player correspondingly loses one unit. If there is no couple, then no one gets anything."

The TGEB analysis of a generalization of the Majority Game is indeterminate in two senses:

• An uncountably infinite number of solution sets of imputations exist (some of which VMN describe as analogous to discrimination).
• In the most obvious solution, { (1/2, 1/2, -1), (1/2, -1, 1/2), (-1, 1/2, 1/2) }, how much a player gets and whether or not he is in the winning two-person coalition is indeterminate (which of the three imputations is realized is unspecified)

VNM generalize their treatment of zero-sum games to non-zero sum games by introducing a powerless dummy:

"56.2.1. ...any given general [not necessarily zero-sum] game can be re-interpreted as a zero-sum game...Our procedure will be to interpret an n-person general game as an n+1-person zero-sum game."

Contrary to Varian, the TGEB treatment of non-zero sum games is a generalization of the TGEB treatment of zero sum games. The VNM solution has come to be known as a solution to cooperative games. (If one sets aside his analysis of bargaining, Nash treats non-cooperative games.) Trivially, only one set of imputations is a solution to a zero-sum two-person game. There is only one imputation in that set, and that imputation is equivalent to the minimax solution.

TGEB has lots of interesting asides and suggestions that relate to later ideas. For example, VNM suggest an alternative treatment in which an external enforcement mechanism for (contracts between players in) cooperative games is not needed. In this alternative treatment of iterative play, cooperation emerges spontaneously:

"21.2.3. If our theory were applied as a statistical analysis of a long series of plays of the same game - and not as the analysis of one isolated play - an alternative interpretation would suggest itself. We should then view agreements and all forms of cooperation as establishing themselves by repetition in such a long series of plays.

It would not be impossible to derive a mechanism of enforcement from the player's desire to maintain his record and to be able to rely on the record of his partner. However, we prefer to view our theory as applying to an individual play. But these considerations, nevertheless, possess a certain significance in a virtual sense. The situation is similar to the one which we encountered in the analysis of the (mixed) strategies of a zero-sum two-person game..."

I don't think this idea works for all cooperative games. But one can see here some ideas of evolutionary game theory.

I read TGEB, particularly the first chapter, as hostile to neoclassical economics. VNM disparage the idea that a model of Robinson Crusoe can tell us much about social phenomena. And they cast doubt on the idea that imitating the mathematical methods used in physics will bring much progress in economics.

References

• Hal R. Varian (2002). "Economic Scene; You've Seen the Movie. Now Just Exactly What was It that John Nash had on his Beautiful Mind", New York Times, 11 April.
• John Von Neumann and Oscar Morgenstern (1953). Theory of Games and Economic Behavior, Third Edition, Princeton University Press.

Chaotic Cobwebs (Part 1)

1.0 Introduction

This post duplicates an example in Richard M. Goodwin's Chaotic Economic Dynamics (Oxford University Press, 1990). At least, I think it does, but without the typographic errors that I think are in Goodwin's book. My Figure 3 is Goodwin's Figure 2.1, and my Figure 2 is Goodwin's Figures 2.2, and 2.3.

I have no plans to prepare a Part 2 to post later. But I describe in the conclusion below why there should be a Part 2.

2.0 Supply and Demand

This model is a partial equilibrium model with well-behaved supply and demand curves. It is an internal exploration of a mainstream textbook model. The demand curve shows the price that must instantaneously prevail if the quantity on the market is to be sold:

(1)

where p(t) is the price of the commodity at time t and q(t) is the quantity supplied or demanded.

Time is discrete in this model, and the supply curve contains a lag. Firms plan the quantity to supply in the next period based on the price in this period:

(2)

The supply curve shows "adaptive expectations". Economists such as Lucas have criticized the assumption of adaptive expectations. I think that critique may be inapplicable in a model with the behavior illustrated in Figure 5 below.

It's easy enough to solve for equilibrium, in which the quantity supplied and the quantity demanded are equal and do not change through time. Equation 3 gives the equilibrium quantity:

(3)

Figure 1 illustrates. The supply and demand curves are shown. The solid dot is the equilibrium. A hint at the dynamics is also shown. At time t, the indicated quantity is thrown on the market. One reads the price at that time off the demand curve. The quantity supplied in the next period is found from drawing a horizontal line from that intersection with the demand curve to the supply curve. This point of intersection with the supply curve is the quantity supplied in the next period. Proceeding in this way, one draws a figure that resembles a cobweb. Thus, this model is known as the cobweb model.

Figure 1: Supply and Demand

I have explained the dynamics of this model above. One can approach the story with algebra and obtain a difference equation:

(4)

Goodwin suggests redefining quantity as the deviation from the equilibrium quantity:

(5)

where Q(t) is the redefined quantity. Equation 6 gives the difference equation in terms of the time path of the redefined quantity variable:

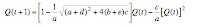(6)

3.0 Numerical Exploration of a Special Case

Goodwin considers the special case where the parameters b and e are both zero. Under this special case, the difference equation becomes considerably simplified:

(7)

Equation 7 resembles the logistic equation. As a start at exploring the dynamics of Equation 7, consider the case where a is unity, c is 3/5, and d is 21/20. (Update: Parameters were originally specified incorrectly.) Figure 2 shows time paths for two arbitrary initial values of the redefined quantity. Both time paths converge to a two-period limit cycle. The upper extreme of the blue time path continually falls, while the upper extreme of the red path continually rises. They meet in the limit at one point in the limit cycle. The lower extremes, shown in FIgure 2, converge to the other point in the limit cycle.

Figure 2: Time Paths of Redefined Quantity

Figure 3 shows another method for illustrating these paths. The difference equation is graphed along with a 45-degree line through the origin. One starts at an initial point along the abscissa. Drop a line to the graph of the difference equation. The value of the ordinate at this intersection with the difference equation shows the value of the redefined quantity variable at the next instant in time. Draw a horizontal line from this intersection to the 45-degree line. The value of the abscissa at this intersection to the 45-degree line is, of course, the value of the redefined quantity variable at the next instant in time. Continually in this way, one can easily trace out a time path graphically. The limit cycle is drawn in Figure 3.

Figure 3: Phase Space for These Paths

Structural dynamics concerns how the limiting behavior varies with the parameters of a difference or differential equation. Here I only consider the effects of a fall in a. Accordingly, Figure 4 shows the result when a is set to 7/10, with the other parameters as in Figure 3. The limit cycle has split into a cycle of period four. This period doubling sort of bifurcation is a common approach to chaos. For some lower values of a, the cycle will have periods eight, sixteen, thirty-two, etc. Figure 5 shows the result when a is 2/3. I believe Figure 5 is an example of chaos, where the limit is a non-wandering set with a fractal structure. (With more exploration, I would like to see a limit cycle of period three, or some other odd value. (Update: Try a as 0.57.) As I understand the mathematics, period doubling can only lead to such a limit cycle with intervening chaos.)

Figure 4: Phase Space for Period Four Cycle

Figure 5: Phase Space Showing Chaos

4.0 Conclusion

The above exposition begins with a common introductory model in economists. And it ends with mathematical chaos. Chaos is shown in a special case in which both the demand and the supply curves go through the origin. A supply curve going through the origin, although a special case, is quite reasonable in economics. It is not economically sensible for the demand curve to go through the origin.

If there were to be a part 2 for this post, it would demonstrate the possibility of chaos in an economically relevant parameter range. One would want the demand curve to be declining throughout the first quadrant as well as intersecting the price axis at a strictly positive price. And one would want the strange attractor to lie entirely in the first quadrant for the price and untransformed quantity variables. But I haven't done enough numerical exploration yet.

Walras, Poincaré, Jaffé, and Mirowski

A couple of posts from Sean Carroll led me to recall some of the interactions between economists and mathematical physicists. One interaction I find of interest is between Walras and Poincaré. Walras’ translator, William Jaffé describes some of the correspondence between the two. Jaffé even quotes one of Poincaré's letters:

"Your definition of rareté [marginal utility] impresses me as legitimate. And this is how I should justify it. Can satisfaction be measured? I can say that one satisfaction is greater than another, since I prefer one to the other, but I cannot say that the first satisfaction is two or three times greater than the other. That makes no sense by itself and only some arbitrary convention can give it meaning. Satisfaction is therefore a magnitude but not a measurable magnitude. Now is a non-measurable magnitude ipso facto excluded from all mathematical speculation? By no means. Temperature, for example, was a non-measurable magnitude – at least until the advent of thermodynamics which gave meaning to the term absolute temperature. The measurement of temperature by the expansion of mercury rather than the expansion of any other substance was nothing but an arbitrary convention. One could just as well have defined temperature by any function of temperature … provided that the function was monotonically increasing. Similarly you [on your side] can define satisfaction by any arbitrary function provided the function always increases with an increase in the satisfaction it represents.

Among your premises, there are a certain number of arbitrary functions; but once given these premises you have the right to draw consequences from them mathematically. If the arbitrary functions still appear in the conclusions, the conclusions are not false, but they are totally without interest because they depend upon the arbitrary conventions made at the start. You ought, therefore, to do your utmost to eliminate these arbitrary functions and that is what you are doing…

…I can tell whether the satisfaction experienced by the same individual is greater under one set of circumstances than under another set of circumstances; but I have no way of comparing the satisfactions experienced by two different individuals. This increases the number of arbitrary functions to be eliminated.

When I spoke of the 'proper limits', that is not all I wanted to say. What I had in mind was that every mathematical speculation begins with hypotheses, and that if such speculation is to be fruitful, it is necessary (as in applications to physics) that one be aware of these hypotheses. If one forgets this condition, one oversteps the proper limits. For example, in mechanics one often neglects friction and assumes the bodies to be infinitely smooth. You, on your side, regard men as infinitely self-seeking and infinitely clairvoyant. The first hypothesis can be admitted as a first approximation, but the second hypothesis calls, perhaps, for some reservations." -- Henri Poincaré (1901)

Jaffé points out that some of Poincaré’s coments foreshadow later developments in economics: revealed preferences and ordinal utility.

Jaffé published his article in 1977. He mentions that Walras initiated this correspondence after being criticized by the mathematician Hermann Laurent, but Jaffé does not explain Laurent's criticism. Since then, Mirowski (1989) has cast new light on this criticism. According to Mirowski, Laurent, in correspondence with Walras and Pareto, queried these neoclassicals about integrability and why economists felt they were justified in assuming utility was the potential of a conservative vector field.

Mirowski does not mention Poincaré's correspondence with Walras. I’d like to see an analysis of this correspondence fromm Mirowski’s viewpoint. I would not expect to see something from Mirowski. He's gone on to other aspects of the history of mainstream economics.

As I understand it, Poincaré, in addition to all of his other accomplishments, was on the verge of discovering the special theory of relativity, but Einstein arrived there first. Poincaré is also cited in the mathematics of dynamic systems. So I expect that he understood the mathematics of vector fields quite well. Did he raise any questions about integrability and conservation laws in his correspondence with Walras?

References

• William Jaffé (1977). "The Walras-Poincaré Correspondence on the Cardinal Measurability of Utility", Canadian Journal of Economics, V. 10 (May): 300-307.
• Neil De Marchi (editor) Non-Natural Social Science: Reflecting on the Enterprise of 'More Heat than Light', Duke University Press.
• Philip Mirowski (2002). Machine Dreams: Economics Becomes a Cyborg Science, Cambridge University Press.
• Philip Mirowski (1989). More Heat Than Light: Economics as Social Physics, Physics as Nature's Economics, Cambridge University Press.
• Léon Walras (1954). Elements of Pure Economics (Trans. by William Jaffé), Ricard D. Irwin.

Neither Econophysics Nor Neoclassical Economics

Some time ago I mentioned Philip Ball's commentary on Gallegati, Keen, and Lux's critique of econophsyics. Cosma Shalizi now has related comments on econophysics and neoclassical economics.

Price Theory Unstudied By Mainstream Economists

This seems hard to credit:

"if current graduate students know anything of price theory, it would have had to have been self-taught, because it is no longer on the curriculum on the 'best' American departments. (Except Chicago where it hangs in by a whisker...)" -- Angus Deaton (2007). "Letter from America - Random Walks by Young Economists", Royal Economic Society Newsletter (April)

Instead, economists study how to statistically analyze intrument variables. (I hope D-Squared will find the reference of interest.)

Judging A Book By Its Back Materials

I simple way of deciding whether one wants to persue reading a paper or book is to look at its bibliography. If it is on a topic that one is interested in and lacks certain references, one might put a low priority on reading it.

I get an ambiguous conclusion in the case of Steven Landsburg's "The Methodology of Normative Economics". From the introduction, I see that Landsburg argues that normative goals cannot be imposed exogenously. People care what a central goal-setting authority does, and the authority must account for that in setting his goals. The reference I look for here is Amartya Sen's "The Impossibility of a Paretian Liberal" (Journal of Political Economy, V. 78, N. 1 (Jan.-Feb. 1970): 152-157). And Landsburg is lacking. But he does reference a later Sen paper that I do not know. Perhaps Sen summarizes his earlier work there.

I get a negative conclusion when looking at Roger Farmer's draft book on old Keynesian economics. Farmer says he presents a model in which the level of economic activity is determined by "animal spirits." This is an allusion to chapter 12 of the General Theory, but Farmer's bibliography lacks any references putting forth a Post Keynesian reading, as far as I can see. Authors I look for include A. Asimakopulos, Victoria Chick, Coddington, Paul Davidson, and Joan Robinson.

And I get a negative conclusion for Claudia Goldin and Lawrence Katz's "Long-Run Changes in the U.S. Wage Structure: Narrowing, Widening, Polarizing". This paper looks at skill-biased technological change. Here I find lacking the failure to reference James Galbraith, such as his book Created Unequal. (Goldin and Katz do reference a number of authors I respect.)

I realize that authors put out drafts just to get these sort of comments. One wants to know if there are elements of a literature on topic that one has missed.