| Figure 1: An Example of Temporal Dynamics for the Logistic Equation |
This post illustrates some common properties of two dynamical systems, chosen out of a large class of such systems. Two quite different functions are drawn, and I demonstrate that, qualitatively, certain behavior arising out of these functions looks quite alike. Furthermore, I point out a mathematical argument that a certain quantitative constant arises for both functions.
I do not claim that the iterative processes here characterize any specific economic model (but see here and here) or physical process. Feigenbaum (1980) mentions "the complex weather patterns of the atmosphere, the myriad whorls of turmoil in a turbulent fluid, [and] the erratic noise in an electronic signal." Such processes have an emergent macro behavior consistent with a wide variety of micro mechanisms. The mathematical metaphors presented in this post suggest that if economic phenomena were described by complex dynamic processes, economists should then reject microfoundations, reductionism, and strong methodological individualism.
2.0 The Logistic EquationThis post is about the analysis of a sequence x0, x1, x2, ... in discrete time. Successive points in this sequence are defined by the repeated iteration of a function fi. (The index i allows one to specify a specific function.) The first few terms of the time series are defined as follows, for a given index i and a given initial value x0:
x1 = fi(x0)
x2 = fi(x1) = fi(fi(x0))
x3 = fi(x2) = fi(fi(fi(x0)))
The logistic function is defined as follows:
f1(x) = a x(1 - x), 0 < a < 4.
Note the parameter a. For a given value of a in the indicated region, the long term behavior of the iterative process defined above is independent of the initial value. This long term behavior varies dramatically, however, with a. In other words, the long term behavior exhibits a kind of dynamic stability, but is structurally unstable.
The behavior of such a sequence can be nicely illustrated by certain diagrams. Figure 1, above, displays the temporal dynamics for one sequence for one value of the parameter a and one initial value. The abscissa and the ordinate in this diagram both range from zero to unity. The 45-degree line then slopes upward to the right from the point (0, 0) to the point (1, 1). Any distance measured upward on the axis for the ordinate can be reflected through the 45 degree line to project the same distance horizontally on the axis for the abscissa. That is, draw a line horizontally from the Y-axis rightward to the 45 degree line. Then draw a vertical line downward from that intersection with the 45 line to the X axis. You will have measured the same distance along both the abscissa and ordinate.
Values for the time series are shown in the diagram by vertical lines. When projected downward to the axis for the abscissa, one will have a plot of x0, x1, x2, etc. In the case shown in Figure 1, the initial value, x0, is 1/2. The logistic function is shown as the parabola opening downward. A line is drawn upward from the axis for the abscissa to intercept the logistic function. The value of the ordinate for this point is x1. To find this value, as measured on the abscissa, a line is drawn leftward from the point of interception with the logistic function to the 45 degree line. Next, draw a line downward from this point on the 45 degree line to the logistic function. The value of the ordinate for this new point on the logistic function is then x2. The step function in Figure 1 going down to the labeled point is a visual representation of the entire time series. Can you see that, in the figure, all times series for the given value of the parameter a, no matter the initial value, will converge to the labeled point? In the jargon, the times series for the logistic function for this value of a is said to have a single stable limit point.
As a matter of fact, the long term behavior of every time series for the logistic function is generically independent of the initial value. It makes sense then, not to plot the first, say, 20,000 points of the time series and only plot the next say 5,000 points. This would lead to a boring graph for Figure 1; the only point in the non-transient part of the time series would be at the stable limit point. Figure 2 shows a more interesting case, for a larger value of the parameter a. Notice the upside-down parabola now rises to a higher value. Because of the form of the logistic function, the plotted function remains symmetrical around x = 1/2.) For the parameter value used for Figure 2, no stable limit points exist for the time series. Rather, the time series converges to a limit cycle of period 3. That is, the cycle illustrated with the structure with the black lines has three vertical lines and repeats endlessly.

|
| Figure 2: A Cycle with Period 3 for the Logistic Equation |
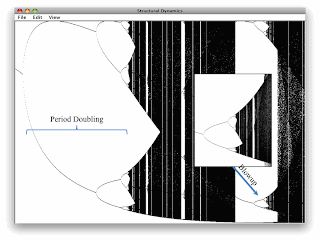
Figures 1 and 2 demonstrate that the limiting behavior of an iterative process for the logistic equation varies with the parameter a. Figure 3 displays this variation from a value of a somewhere under 3.0 to 4.0. In Figure 3, the value of a is plotted along the abscissa. For each value of a, non-transient values of a time series are plotted along the ordinate. To the left of the figure, the time series converges to a single stable limit point. Somewhere to the right, this limit point becomes unstable, and the limiting behavior consists of a cycle of period 2. Moving further to the right - that is, increasing a, limit cycles of period 4, 8, 16, etc. appear. The limit cycle of period 3 shown in Figure 2 corresponds to a parameter value of a somewhere to the center left of the region shown in the blown-up inset.

|
| Figure 3: Structural Dynamics for the Logistic Equation |
In some sense, this is recreational mathematics. Computers these days make it fairly easy to draw a more complete representation of Figure 4 in May (1976). The blow-up in Figure 3 demonstrates that the structural dynamics for the logistic function is fractal in nature. We see the same shape repeated on increasingly smaller and smaller scales. Chaos arises for parameter values of a between the period doubling cascade and the period-3 cycle. (Chaotic behavior is shown in Figure 3 by the dark shaded regions.)
3.0 A Exponential-Logistic EquationI repeated the above analysis for what I am calling an exponential-logistic function:
f2(x) = (x/c) ea(1 - x), 0 < a
where:
c = 1, if a - ln a ≤ 1
c = -1/(a ea - 1), if 1 < a - ln a
This exponential-logistic function was suggested to me by a function in May (1976). I introduced the scaling provided by c such that the maximum value of this function never exceeds unity. This function, like the logistic function, is parametrized by a single parameter, which I am also calling a. Figure 4 shows the non-transient behavior for a specific value of the parameter a for the exponential-logistic function. In this case, a stable limit cycle of period 32 arises.

|
| Figure 4: A Cycle with Period 32 for the Exponential-Logistic Equation |
Notice the exponential-logistic function is generally not symmetric around any value of x; one tail is heavier than the other. Furthermore, it only has a zero at the origin; nothing corresponds to the zero at x = 1 in the logistic function. So, in some sense, it has a quite different form from the logistic function. Yet, as shown in Figure 5, the structural dynamics for iterative processes for the exponential-logistic function are qualitatively similar to the structural dynamics arising from the logistic function. We see the same shapes in Figures 3 and 5, albeit distorted in some sense.
|
| Figure 5: Structural Dynamics for the Exponential-Logistic Equation |
I now report on some quantitative numerical experiments. Table 1, in the second column, shows the smallest value of the parameter a for which I was able to find a limit cycle of the given period for the logistic equation. Cycles of an infinite number of periods - that is, for all positive integer powers of two (2, 4, 8, 16, ...) - exist in the period-doubling region labeled in Figure 3. As suggested by Table 2, the distance between values of a at which period-doubling occurs gets smaller and smaller. In fact all these limit cycles arise before a = 3.5700..., the point of accumulation of a at which chaos sets in. (I do not fully understand the literature on how to calculate the period of limiting cycles for a. I therefore do not report values of a for larger periods than shown in the table, since I do not fully trust my implementation of certain numeric methods.)
| Period | a | Difference | Ratio |
| 2 | 2.9999078 | ||
| 4 | 3.4494577 | 0.449550 | 4.7510 |
| 8 | 3.5440789 | 0.094621 | 4.6556 |
| 16 | 3.5644029 | 0.020324 | 4.6669 |
| 32 | 3.5687579 | 0.004355 | 4.6665 |
| 64 | 3.5696911 | 0.000933 | 4.6666 |
| 128 | 3.5698109 | 0.000200 |
Table 1, above shows, in the third column, the difference between values of a at which period-doubling occurs. The fourth column shows the ratio of successive difference. Theoretically, this ratio converges to δ = 4.669201609... My numeric exploration has found this constant to at least two significant figures.
The convergence of this ratio, over limit cycles for periods of powers of two, is not limited to the logistic equation. Table 2 reports the result of a numeric experiment with the exponential-logistic equation. Here too, the constant δ has been found to two significant figures. Interestingly, the ratio would theoretically converge to the same constant if the two tables were infinitely extended. In fact, δ is a universal mathematical constant, like π or e.
| Period | a | Difference | Ratio |
| 2 | 2.7180077 | ||
| 4 | 4.6016740 | 1.883666 | 2.9506 |
| 8 | 5.2400786 | 0.638405 | 4.2473 |
| 16 | 5.3903856 | 0.150307 | 4.5651 |
| 32 | 5.4233107 | 0.032925 | 4.6456 |
| 64 | 5.4303982 | 0.007087 |
The above analysis can be generalized to many other functions, albeit I do not fully understand how to characterize the class of such functions. Feigenbaum states that the period doubling route to chaos is not limited to one-dimensional processes. I believe it also arises in continuous time systems, as defined by certain non-linear differential equations. Do you find it surprising that a universal constant with wide applicably to physical processes (like year-by-year changes in the population demographics of certain species), has been discovered in the lifetime of many now alive?
References- Keith Briggs (1991). A Precise Calculation of the Feigenbaum Constants, Mathematics of Computation, V. 57, No. 195 (July): pp. 435-439.
- Mitchell J. Feigenbaum (1980). Universal Behavior in Nonlinear Systems, Los Alamos Science (Summer): pp. 4-27.
- Tien-Yien Li & James A. Yorke (1975). Period Three Implies Chaos, American Mathematical Monthly, V. 82, No. 10 (Dec.): pp. 985-992.
- Robert M. May (1976). Simple Mathematical Models with Very Complicated Dynamics, Nature, 261: pp. 459-467.





No comments:
Post a Comment