 |
| Figure 1: Coefficients of Production for the Technology |
This post advances, somewhat, my start at a reconsideration of the dynamics of Overlapping Generations Models (OLGs). Only the production side of a stationary state is considered here. Furthermore, only a very special case - namely, a one-good model - is analyzed here.
I guess the most exciting aspect of this post is an illustration of the claim that the construction of the wage-rate of frontier is useful for the analysis of the choice of technique for "smooth" production functions, not just for discrete technologies. I have never understood, for at least a quarter of a century, why some economists seem to talk as if a fundamental distinction exists between such models. In some contexts, some conclusions differ. But it seems to me to be silly to say that the Cambridge Capital Controversy turns around an empirical question on the degree of substitutability of inputs in production.
2.0 Specification of TechnologyConsider a simple economy in which corn is produced from inputs of labor and corn. Assume the existence of Constant Returns to Scale (CRS). A technique is specified by an ordered pair of coefficients of production, where each ordered pair is from a set containing a continuum of such ordered pairs:
{ [a0(s), a1(s)] | 0 < s < 1}
where:
a0(s) = 1/(A s)1/(1 - α)
a1(s) = s1/α
and α and A are specified positive parameters such that:
0 < α < 1
Figure 1 graphs the coefficients of production as a function of the index s. All graphs are draw for a value of α of 1/4 and of A of 5.
3.0 Derivation of the Cobb-Douglas Production FunctionThe above specification of the technology shows, for a unit output of corn, a smooth trade-off of inputs of labor and corn inputs. This specification of technology allows for the derivation of a conventional production function. The following is an equation for a unit isoquant for this technology:
1 = A [a1(s)]α [a0(s)]1 - α
Define:
- Q is (gross) corn (bushels) output.
- L is labor (person-years) input.
- X is (seed) corn input.
From CRS, it follows:
Q = A [Q a1(s)]α [Q a0(s)]1 - α
Or:
Q = A Xα L1 - α
The last equation above is how the (in)famous Cobb-Douglas production function is typically represented. So the specification of technology used in this post is a (non-unique) representation of a Cobb-Douglas production function.
4.0 Analysis of the Choice of TechniqueFor a given technique, Sraffa's price equations become one equation:
a1(s)(1 + r) + a0(s) w = 1
where:
- r is the rate of profits
- w is the yearly wage (in units of bushels per person-year).
The price equation embeds the assumptions that production of corn requires a year to complete and that labor is paid out of the yearly harvest. One can derive a wage-rate of profits curve from the price equations:
w(r, s) = [1 - a1(s)(1 + r)]/a0(s)
In this case, each wage-rate of profits curve is a straight line. Figure 2 shows three selected wage-rate of profits curves.
 |
| Figure 2: Wage-Rate of Profits Curves and Their Frontier |
Figure 2 shows, in violet, the outer wage-rate of profits frontier. When firms choose the cost-minimizing technique in a steady state, the economy will lie on this curve. (In this case, with a continuum of techniques, each point on the frontier is a non-switch point.) A closed-form expression for the wage-rate of profits frontier is easily derived. The First Order Condition (FOC) for the choice of technique can be expressed as equating the derivative, with respect to the index variable, of the wage-rate of profits curve to zero:
dw/ds = 0
The FOC yields an equation which can be solved for the index variable:
s(r) = [α/(1 + r)]α
So the coefficients of production, for the cost-minimizing technique, can be found as functions (Figure 3) of the rate of profits:
a0(r) = [1/A1/(1 - α)] [(1 + r)/α]α/(1 - α)
a1(r) = α/(1 + r)
Thus, the desired expression for the wage-rate of profits frontier is:
w(r) = (1 - α) A1/(1 - α) [α/(1 + r)]α/(1 - α)
In this special case, the desired amount of labor per unit output is higher, the lower the wage. Likewise, the desired amount of the capital good per unit output is lower, the higher the rate of profits. These results do not generalize to multi-commodity models.
 |
| Figure 3: Optimal Coefficients of Production |
In this special case, the ratio of the value of capital goods to labor can be calculated in physical terms, without addressing a question of valuation. That is, the capital-labor ratio, as a function of the rate of profits (Figure 4), is easily derived:
I(r) = a1(s(r))/a0(s(r)) = [α A/(1 + r)]1/(1 - α)
In this special case, the capital-labor ratio is a downward-sloping, single-vauled function of the rate of profits. These properties do not generalize, either.
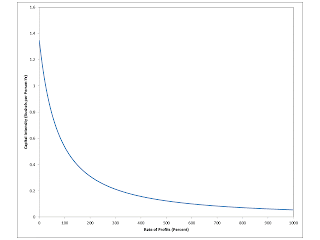 |
| Figure 4: Capital Intensity |




2 comments:
It is indeed an elegant model! Two comments: (1) discrete techniques influence the behaviour of the system. A switch to another technique leads to significant changes in the quantities of production factors. This causes shocks in the economic structure. It is a source of instability. For the enterprises, the shocks create uncertainty, which makes them reluctant to perform the switch. (2) I would think that each point on the frontier must be a switch point. Otherwise it would be impossible to switch. The continuous curve would be the hull of the frontier, and is never a frontier itself. Therefore it seems that dw/ds does not exist on the frontier (consisting of switch points). I admit that this is strange, because in the limit all switch points would coincide.
Thanks for the comment.
I certainly know of at least one theorem that does not apply to discrete technologies. But I hope to show (or at least explore) the claim that the divide is not that sharp.
Solow also mistakenly claimed that every point in a model like this must be a switch point. But, if that is so, you should be able to provide more than one set of cost-minimizing coefficients of production at each point.
Post a Comment