|
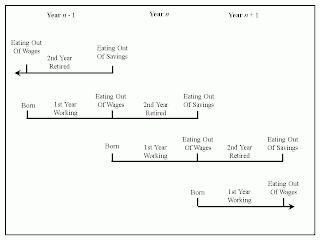
| Overlapping Generations |
The theory of comparative advantage does not justify free trade in consumer goods. The mainstream textbook presentation is just logically mistaken. I have proven these claims in a paper building on work staring from a third of a century ago. My paper provides a numeric example. I have previously presented the production side of another numeric example here. My paper concludes with an utility-maximizing closure, but I have decided that this part of my paper could be improved. Accordingly, this post provides a simple overlapping generations example to combine with my previous numeric example in the blog post.
2.0 Overlapping GenerationsAccordingly, consider an Overlapping Generations (OLG) model in which each agent lives for two years. Each agent works in the first year of their life and is retired in the second year. They are paid their wages at the end of the year in which they work. They can choose to save some of their wages for consumption at the end of the second year of their life.
Suppose each agent has the following utility function:
U(x20, x21, x40, x41) = (x20 x40)γ(x21 x41)1/2 - γ, 0 < γ < 1/2
where:
- x20 is the quantity of wine consumed at the end of the first year of the agent's life.
- x21 is the quantity of wine consumed at the end of the second year of the agent's life.
- x40 is the quantity of silk consumed at the end of the first year of the agent's life.
- x41 is the quantity of silk consumed at the end of the second year of the agent's life.
In the numeric example, 4,158 agents are born each year in country A, and 3,969 agents are born each year in country B. Since wine and silk enter the utility function symmetrically, equal amounts of wine and silk are consumed each year in each country in a stationary state, given an (international) price of silk of unity. Although all agents are assumed identical in a given country, agents may vary across countries. In particular, difference in the parameter γ in the utility function between countries can rationalize the difference in income distribution between the two countries in the example.
It remains to outline in more detail a demonstration of these claims. The agent is faced with the following mathematical programming problem:
Given p, w, and r
Choose x20, x21, x40, x41
To maximize U(x20, x21, x40, x41)
Subject to:
(x20 + px40)(1 + r) + (x21 + px41) = w(1 + r)
x20 ≥ 0, x21 ≥ 0, x40 ≥ 0, x41 ≥ 0
Three independent marginal conditions arise in solving this optimization problem:
(∂U/∂x20)/(∂U/∂x21) = 1 + r
(∂U/∂x20)/(∂U/∂x40) = 1/p
(∂U/∂x21)/(∂U/∂x41) = 1/p
These three marginal conditions, along with the budget constraint, constitute a system of four equations in four variables. Its solution is:
x20 = γ w
x21 = (1 - 2 γ) w (1 + r)/2
x40 = γ w/p
x41 = (1 - 2 γ) (w/p) (1 + r)/2
The total demand for, say, wine to consume at the end of each year is summed over workers and retirees in that year:
X2 = lTotal(x20 + x21)where:
- X2 is the quantity of wine demanded in a given country each year.
- lTotal is the annual endowment of labor in the given country.
A similar equation arises for the demand, X4, for silk:
X4 = lTotal(x40 + x41)
One can use the above equations to close the with-trade case in my numeric example, at least in cases where the interest rate is not too big. In the latter sort of cases, I might want to consider models in which agents either work or retire for more than one year. At any rate, agents, in this extension, will live for more than two years, and more than two generations will be alive in any given year.
3.0 AutarkyAn autarky for my model of production is closed with this model of utility-maximization. A degree of freedom does not exist. The condition that both wine and silk both be produced leads to the determination of the wage and the price of silk as a function of the interest rate.
The equality of savings and investment is an equilibrium condition. In the above model, savings, S, is:
S = lTotal(w - x20 - p x40)
Using the aforementioned price equations, one can express savings as:
S = lTotal(1 - 2 γ)/(l1R + l2),
where:
R = 1 + r
Investment, I, is a numeraire quantity of capital, found from an indirect demand from consumer goods:
I = (l1 X2 + l3 X4)w
Once again, using the price equations, one can express investment as a function of model parameters and the interest rate:
I = lTotal[2 γ + (1 - 2 γ)R](2l1l3R + d)/[2 (l1R + l2)2 (l3R + l4)]
where:
d = l1 l4 + l2 l3
The equilibrium interest rate and, hence, the (domestic) price of silk and wage are found by equating savings and investment. I am hoping that this solution is sufficient to guarantee the quantities demanded of wine and silk lie on the Production Possibilities Frontier (PPF).
4.0 Numeric ValuesIn the numeric example, prices are specified. Wine is taken as the numeraire. The price of silk on the international market is unity. The wage is (1/200) units wine per person-year in country A and (1/194) units wine per person-year in country B. The interest rate is 20% in country A and 5% in country B. Let the parameter of the utility function be as follows in the two countries:
γA = 47/99
γB = 89/378
Then the quantities of wine and silk demanded for consumption are as in Table 1. But the entries in Table 1 are taken from my numeric example. So this utility-maximization model does, in fact, close the model of production and international trade used in the numeric example, at least in the with-trade case. When I worked out the autarky case, though, I ended up with a negative interest rate in the two countries.
| With-Trade Specialization | ||
| Endowments | Country A | lTotal,A = 4,158 person-years |
| Country B | lTotal,B = 3,969 person-years | |
| International Price of Silk | p = 1 Unit wine per Unit silk | |
| Wine Consumption | Country A | 10 1/2 Units wine |
| Country B | 10 1/2 Units wine | |
| Total | 22 Units wine | |
| Silk Consumption | Country A | 10 1/2 Units silk |
| Country B | 10 1/2 Units silk | |
| Total | 22 Units silk | |
I have constructed a numeric example in which trade in consumer goods unambiguously leaves the Production Possibilities Frontier (PPF) rotated inward, as compared with autarky, for country A. And I have rationalized, in a way consistent with neoclassical theory, why a positive interest rate exists and varies between countries in the with-trade equilibrium. But I have not found an example in which the corresponding autarkic equilibrium is consistent with positive interest rates in the two countries in the example.
Appendix: Definition of Parameters and Variables- γ: A parameter of the agent's utility function.
- γA: A parameter of the agent's utility function for country A.
- γB: A parameter of the agent's utility function for country B.
- I: National investment.
- R: 1 + r.
- S: National savings.
- U(x20, x21, x40, x41): The agent's utility function.
- X2: The quantity of wine demanded yearly in a given country, summed across all agents.
- X4: The quantity of silk demanded yearly in a given country, summed across all agents.
- d: A parameter relating to the relative labor intensity of wine and silk production.
- lTotal: The total endowment of labor in a given country; that is, the number of agents born each year.
- x20: The quantity of wine the agent consumes at the end of the first year of his life.
- x21: The quantity of wine the agent consumes at the end of the second year of his life.
- x40: The quantity of silk the agent consumes at the end of the first year of his life.
- x41: The quantity of silk the agent consumes at the end of the second year of his life.
- p: The price of silk (in unit's wine per unit silk).
- r: The interest rate.
- w: The wage (in unit's wine per person-year).




No comments:
Post a Comment