|
| Figure 1: Prices of Production |
1.0 Introduction
This post presents a new kind of fluke case in the analysis of the choice of technique, at least new to me.
I call this a pattern for requirements for use, and it can arise only in a case of joint production. My graphs
in this post have some incomprehensible notation, since I am currently exploring perturbing parameters, in
line with my research agenda.
I know that perturbing the requirements for use removes the indeterminancy in this example.
2.0 The Givens
For this example, the data consist of the available technology and the proportions in which the two produced commodities,
corn and silk, enter into the commodity basket specified by the requirements for use. I also choose a numeraire. The example
is a perturbation of problem 8.2 in Kurz and Salvadori (1995).
Table 1 specifies a constant returns-to-scale technology. In each of three processes known to managers of firms at a given time,
laborers work with inputs of corn and silk to produce outputs of corn, silk, or both. The inputs are completely used up in
producing the output, and all three processes are assumed to take a year to complete. Since two commodities are produced
in this numerical example, a technique consists of at most two processes. Table 2 lists the techniques and
the processes corresponding to each technique.
Table 1: Coefficients of Production for The Technology
| Input | Process |
| I | II | III |
| Labor | 1 Person-Yr. | 1 Person-Yrs | (e/16) Person-Yr. |
| Corn | 1 Bushel | 1 Bushel | 1 Bushel |
| Silk | 1 Sq. Meter | 1 Sq. Meter | 1 Sq. Meter |
| Output | |
| Corn | 3 Bushels | 5 Bushels | 0 Bushel |
| Silk | 3 Sq. Meters | 0 Sq. Meter | 5 Sq. Meters |
Table 2: Techniques of Production
| Technique | Proceses |
| Alpha | (I), (II) |
| Beta | (I), (III) |
| Gamma | (II), (III) |
| Delta | (I) |
| Epsilon | (II) |
| Zeta | (III) |
The requirements for use are such that equal quantities of corn and silk are required. The numeraire consists of
a commodity basket of one bushel corn and one square meter of silk.
3.0 Quantity Flows
Which techniques can satisfy the requirements for use? Suppose, contrary to the
specification, that requirements for use specified that more bushels of
corn be supplied than square meters of silk. The Alpha technique technique could satisfy these requirements for use,
with Process I and Process II both being operated at a positive level of operations. As the requirements for corn
declined, the relative level of operation of Process II would decline. The Alpha technique satisfies the given
requirements for use with Process II operated at a level of zero. This is a corner case in which Process II still
contributes an equation to the price system.
By a symmetric argument, the Beta technique can also satisfy the requirements for use. Process III is operated
at a level of zero in the Beta techniquye.
The Gamma technique can satisfy any composition of the requirements of use, as in the theory of single
production. So it can satisfy the requirements for use in this case, too.
The Delta technique can satisfy any requirements for use, as well. However, when the requirements for
use specify an unequal number of bushels corn and square meters of silk, one commodity is in excess
supply and its price of production is zero.
Neither the Epsilon nor the Zeta technique can satisfy the requirements for use when the net output
must contain a positive quantity of both commodities.
4.0 Prices of Production
But being feasible, in the sense that a technique can satisfy the requirements for use, is not
sufficient for a technique to be cost-minimizing. Prices of production must be considered,
as in models of the production of commodities with single production. Prices of production
vary with distribution and the technique. Figure 1, at the top of this post, graphs the price
of corn for the three techniques which contribute two equations, in addition to the equation
specifying the numeraire, to determine the four price variables (price of corn, price of
silk, the wage, and the rate of profits).
4.1 The Alpha Technique
Suppose the Alpha technique is in operation. The wage can range from zero to two numeraire units per person-year.
Figure 2 shows that the Alpha technique is not cost-minimizing at low rates of profits, but is cost-minimizing at high
rates of profits. If, at low rates of profits, Process III replaces I, the Gamma technique will be adopted.
If it replaces Process II, the Beta technique is adopted. But the Beta technique is not cost-minimizing at low rates of profits.
(In a model of single production, it is unambiguous which process is replaced when a new process is
introduced into a technique.)
|
| Figure 2: Extra Profits with Prices for the Alpha Technique |
4.2 The Beta Technique
On the contrary, suppose the Beta technique is in operation. Figure 3 shows that this technique is cost-minimizing
only at high rates of profits. At low rates of profits, firms will have an incentive to operate Process II.
If they replace Process III by Process II, firms will be operating the Alpha technique. The above analysis
has shown that the Alpha technique would not be cost-minimizing in this range of the rate of profits. If Process I
is replaced by Process II, firms would be operating the Gamma technique.
|
| Figure 3: Extra Profits with Prices for the Beta Technique |
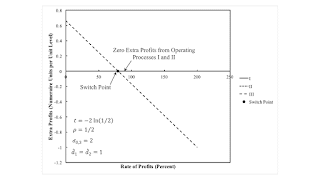
4.3 The Gamma Technique
The Gamma technique is cost-minimizing at low rates of profits. Figure 4 shows extra profits for prices for the
Gamma technique. Both the Alpha and the Beta technique are cost-minimizing at high rates of profits. Extra profits
can be made in operating Process I at Gamma prices for high rates of profits. Firms would find it profitable to
replace either Process III or Process II, resulting in either the Alpha or the Beta technique, respectively.
|
| Figure 4: Extra Profits with Prices for the Gamma Technique |
4.4 The Delta Technique
I am going to present the Delta technique in more detail. For Process I to neither make extra profits nor
to incur extra costs, the following equality must obtain.
(p1 + p2)(1 + r) + w = 3 p1 + 3 p2
The specification of the numeraire yields the following equation:
p1 + p2 = 1
For the Delta technique to be cost-minimizing, the two equations above must hold, extra profits must not
be obtainable in operating Process II, and extra profits must not be obtainable in operating Process III.
Prices drop out of the equation arising out of the requirement that Process I neither obtains
extra profits nor incurrs extra costs. The wage is an affine function of the rate of profits:
w = 2 - r
The above wage curve is identical with the wage curves for the Alpha and the Beta techniques.
For the Delta technique to be cost-minimizing, firms must not be able to obtain extra profits
in operating Process II. This condition yields an inequality:
p1 ≤ 1 + r + w
Substituting the wage curve and re-arranging terms yields an upper bound on the price of
corn:
p1 ≤ 3/5
That is, the price of corn cannot exceed the price of corn falling out of the Alpha technique.
This inequality is shown by the upper bound of the shaded region in Figure 1 at the top
of this post.
The condition that firms cannot obtain extra profits in operating Process III also
yields an inequality:
p2 ≤ 1 + r + (e/16) w
Or the price of corn cannot fall below a lower bound:
(1/80)[64 - 2 e - (16 - e)r ≤ p1
This inequality is shown by the lower bound of the shaded region in Figure 1.
The Delta technique can be consistent with cost-minimizing for any price
of corn in the shaded region, including the boundaries. The two constraints
combined impose a lower bound of the rate of profits:
[2 (8 - e)]/(16 - e) ≤ r
The lower bound on the rate of profits is the rate of profits at the switch point.
As with the Alpha, Beta, and Gamma techniques, one can plot extra profits
versus the rate of profits for all processes, given the price system for the
Delta technique. Since the Delta technique has an extra degree of freedom,
one must choose a price, as well as, say, the rate of profits for such an
analysis. Figure 5 shows such a graph for a price of corn of 3/5 numeraire
units per bushel. The switch point here is at the same rate of profits
as for the switch point shown in Figures 2 and 3. For rates of profits
below the switch point, firms will want to adopt the Gamma technique.
For rates of profits above the switch point, the Delta technique
is cost-minimizing, but not uniquely so. Firms would also be
willing to adopt the Alpha technique.
|
| Figure 5: Extra Profits with One Set of Prices for Delta |
But suppose the price of corn happens to be 1/2 numeraire units per
bushel. Figure 6 plots extra profits in the three processes against the
rate of profits. Firms will no longer be willing to choose to operate
Process II along side Process I for some distribution of income. Costs exceed
revenues for Process II, whatever the rate of profits.
|
| Figure 6: Extra Profits with Another Set of Prices for Delta |
For low rates of profits, the Delta technique is not cost-minimizing;
firms will want to adopt the Beta technique. The "switch point" in Figure
6 is to the right of the switch point shown in all the other graphs in this
post. From Figure 3, we know the adoption of the Beta technique is not the
end of the story if the rate of profits lies below the rate of profits
in the original switch point. For rates of profits between the two
"switch points", prices must adjust until no extra profits can be
obtained by operating the Beta technique. For rates of profits above
the new "switch point", the Delta technique is uniquely cost minimizing
at these prices and distribution of income. The Beta and Delta techniques
are both cost-minimizing only at the new "switch point".
4.5 Summary
I find the possibilities in joint production confusing. I am fairly convinced of
the above analysis, but I would not be surprised if my exposition could be
improved. Anyway, here is a summary of the analysis of the choice of technique
for this numerical example:
- When the rate of profits is smaller than the rate of profits at the switch point (or, equivalently, the wage is
greater than the wage at the switch point), the Gamma technique is uniquely cost-minimizing. Prices are
determined, given, say, the wage.
- When the rate of profits is larger than the rate of profits at the switch point (or the wage is
lower than the wage at the switch point), the Alpha, Beta, and Delta techniques can all be cost-minimizing.
Prices are indeterminate, with the price of corn confined to lie in the limits shown in Figure 1 by the curves
for the Alpha and Beta techniques. Processes II and III in the technology are each operated at a
level of zero, whatever the technique.
- When the rate of profits and the wage are as at the switch point, the Alpha, Beta, Gamma, or Delta
technique are all cost-minimizing. Prices are determined, with a bushel corn priced at 3/5 numeraire
units and a square meter of silk at 2/5 numeraire units.
5.0 Conclusion
This is a fluke case. If the proportions in which corn and silk enter into the commodity basket specified by
requirements for use are varied at all, the indeterminancy of prices associated with a low wage vanishes.
If bushels of corn exceeds square meters of silk in requirements for use, the Alpha and Gamma techniques
are feasible. The Beta technique cannot satisfy the requirements for use. The Delta technique can satisfy
the requirements for use, with an excess supply of silk at a price of zero. But then extra profits would be
available by operating the second process. So only the Alpha or Gamma technique would be cost-minimizing,
depending on income distribution.