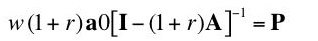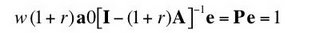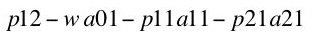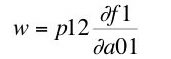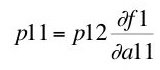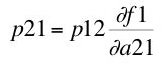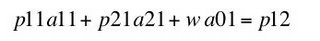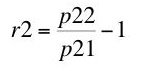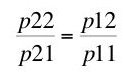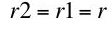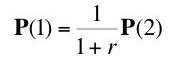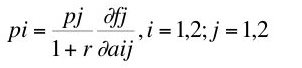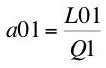3.0 Marginal Conditions Arising From Profit MaximizationPreviously, I outlined a model on an economy in which wheat and corn are produced in yearly production cycles. If the profit-maximizing competitive firm produces wheat, it must solve the following mathematical programming problem:
Given w, P(1), P(2)
Choose a01, a11, a21 to
To Maximize
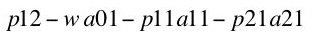 (6)
(6)
Such that

The solution gives the following marginal productivity equations:
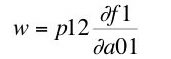 (7)
(7)
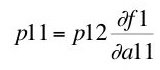 (8)
(8)
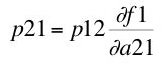 (9)
(9)
In competitive equilibrium, the price of every input is equal to the value of the marginal product for each product.
Pure economic profit must be nonnegative, for if it were negative the firm would have chosen not to produce at all. It works out that pure economic profit cannot be positive either. Equation 10 states that pure economic profit is zero in the wheat-producing industry:
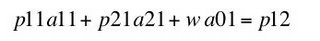 (10)
(10)
An analogous set of three marginal productivity equations and a zero economic profit condition arises from analyzing corn-producing firms.
4.0 Interest Rates In Steady StatesConsider the following definitions:
 (11)
(11)
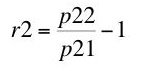 (12)
(12)
These are known as the own rates of interest of wheat and corn, respectively.
In a long run equilibrium, the quantities of wheat and corn inputs are not given. Assume they have been adjusted such that relative spot prices of corn, wheat, and labor remain unchanged from year to year. Almost all economists up until the late 1920s, as far as I am aware, thought of this constancy of relative prices, or an equivalent condition, as a defining property of long run equilibrium.
(It was about then that short-run notions of temporary and intertemporal equilibrium were introduced, and the economists' conceptions became more complex. Mistakes were made by the early neoclassicals. Walras thought he could take endowments of produced goods as given, but still consider an equilibrium with steady-state prices. Others mistakenly wanted to take the quantity of "capital" as given, but have its form, in terms of composition of wheat and corn, be endogenously determined.)
Certainly, we need to introduce some condition relating industries. Anyways, If you think about the condition of stationary spot prices, you will see that if no pure economic profits are possible, relative forward and relative spot prices must be equal:
 (13)
(13)
Otherwise, an agent could buy or sell wheat or corn in the forward market for a year and make a pure economic profit on the spot market at the end of the year.
Therefore:
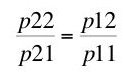 (14)
(14)
Or:
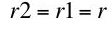 (15)
(15)
where
r is the common own rate of interest for all commodities. It is not a parameter of some unobservable utility function, although it may become equal to some such parameter in equilibrium in special cases. Such a special case could be created by closing this model with utility-maximization by a infinitely-lived representative agent.
The condition of unchanging relative spot prices allows us to remove
P(2) from our equations. We have:
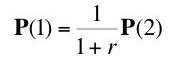 (16)
(16)
The condition of no economic profit gives the following system of two equations:
 (17)
(17)
where I have dropped the time index on the price vector as being no longer needed. The marginal productivity equations become:
 (18)
(18)
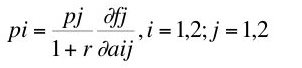 (19)
(19)
So we have a system of eight Equations - the two price equations (17), and the six marginal productivity equations (18) and (19). There are ten choice variables to be determined by the model:
- The wage w
- The common own rate of interest r
- Two prices, P = (p1, p2)
- Six production coefficients a0 and A
I assume it's obvious that the above model generalizes to an
n good model. There are two degrees of freedom. One is closed by selecting the numeraire.
There is no equation equating
r to some mystical, mythical, marginal product of capital.
In the next part, I outline the construction of the so-called factor price frontier.