|
| Figure 1: Isoquants For The Production Function |
1.0 Introduction
I often assume a discrete technology in my demonstrations that what many mainstream economists teach is mostly incoherent balderdash.
Some incompetents have told me that such well-established results "just show
that the particular production functions that you have chosen don't work. This is not a generic result."
So, for my amusement, I will go through a simple
example here to explain how any continuously differentiable production function can be approximated arbitrarily closely
by the production function for a discrete technology.
By the way as far as I know, capital-reversing is consistent with continuously differentiable production functions.
Does the late Emmanuel Farhi's work on this theme make progress on Wolfgang Eichert's work? I sometimes worry
that a serious exploration by a mainstream economist of the Cambridge capital controversy would lead to
psychological depression.
2.0 The Model
I consider a single sector of an economy where, say, Q tons steel are manufactured from
inputs of labor and iron. The managers of firm know of S processes for producing
steel, where each process is characterized by an ordered pair of coefficients of production.
That is, the technology for making steel, T, is defined as:
T = { (a0(s), a(s)) | s = 1, 2, ..., S }
In the sth process, the services of at least a0(s) person-years of labor
and a(s) tons iron must be applied for every ton steel produced.
With only two inputs, I can assume that labor coefficients are ordered to be increasing:
0 < a0(1) < a0(2) < ... < a0(S)
And that iron coefficients are decreasing:
a(1) > a(2) > ... > a(S) > 0
With this specification of technology, one can formulate a linear program (LP). Let L be the
person-years of labor available to this firm, and let X be the tons of iron available.
Define q1, q2, ..., qS to be the
tons steel produced with each of the S processes.
Consider the following LP:
Given T, L, and X, choose q1, q2, ..., qS
To maximize Q = q1 + q2 + ... + qS such that
a0(1) q1 + a0(2) q2 + ... + a0(S) qS ≤ L
a(1) q1 + a(2) q2 + ... + a(S) qS ≤ X
q1 ≥ 0, q2 ≥ 0, ..., qS ≥ 0
Let the solution of this LP be:
Q = F(L, X)
Then F is the production function for steel production.
3.0 Selected Properties of a Production Function
A production function as defined above exhibits constant returns to scale (CRS). Figure 1, at the top of this post, displays isoquants for
a particular technology with S equal to four. Any point in the interior of the line seqment
between (a0(1) Q, a(1) Q)
and (a0(2) Q, a(2) Q), for example, is a switch point. The extremes are non-switching points,
where only one process in the technology is operated.
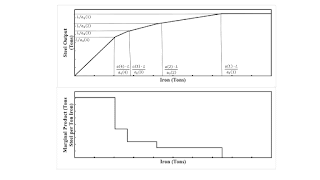
Figure 2 graphs the output of steel as a function of the labor input, given a specified quantity of iron available for input. The
physical marginal product is shown below. The marginal product is non-increasing. The horizontal steps are non-switching points,
and the vertical jumps occur at switch points.
|
| Figure 2: The Marginal Product Of Labor |
In this example, labor and iron inputs are treated formally the same. So, as Figure 3 shows, the graph of the output of steel as a function
of the iron input, and of iron's physical marginal product, look qualitatively the same as the output of steel as a function of the labor
input.
|
| Figure 3: The Marginal Product Of Iron |
Linear programming, as I understand it, is not taught as introductory mathematics. On the other hand, one can explain the above
graphs without knowledge of calculus. Are there still recent introductory textbooks for microeconomics with graphs like the above?
4.0 Conclusions
One can generalize the above to consider a production function for more than two inputs. The processes will not be ordered as above, and isoquants would be graphed in a higher dimensional space. Another generalization would consider multiple production funtions, one for each sector, with given prices for the produced outputs. Given endowments for inputs, also known as 'factors of production', the dual problem assigns shadow prices to the inputs.
Also, endowments are not given in long-period models.
References
- Eichert, Wolfgang. 2014a. Long-period positions in multi-sectoral Cobb-Douglas economies. Metroeconomica 65 (1): 136-153.
- Eichert, Wolfgang. 2014b. Technological Change in Multi-Sectoral Economies: Theoretical Change in Multi-Sectoral Economies. Doctoral thesis, University of Graz.
- Pasinetti, Luigi L. 1977. Lectures on the Theory of Production. New York: Columbia University Press.