
|
| Figure 1: The Wage Frontier at a Four-Technique Patterns |
This post presents another numerical example of one technique replacing another, along the wage frontier, with a perturbation of a model parameter.
In a previous post, I identified three sequences of patterns of switch points in which the wage curves for one technique replaces the wage curve of another. In one of these sequences, a three-technique pattern removes the middle technique from three techniques with wage curves on the wage frontier. A further perturbation of the model parameter of concern results in another three technique pattern, in which the wage curve for a new technique appears in the middle of the wage frontier. In a limiting case of this sequence of patterns, the distance in the parameter space between the two three-technique patterns reduces to zero. A four-technique pattern results.
The parameter that is increased, in this case, is not a coefficient of production. Rather, I consider a model in which barriers to entry, or some such idiosyncratic property of investment in specific industries, results in maintaining specified ratios of the rates of profits among industries. One of these ratios is the parameter that is varied in the numerical example. I have applied my pattern analysis in a limited way to such a model before. By the way, although others have recently analyzed such a model, I find that Ian Steedman outlines this model in his 1977 book, Marx after Sraffa.
This example is more complicated than previous examples of four-technique patterns. At the switch point in which the wage curves for four techniques intersect, processes in two industries are both changed. This is a fluke case - a pattern of co-dimension two, in my terminology. But, in the example, the process in a third industry does not vary with the cost-minimizing techniques around the switch point. The example also illustrates variation in the sequence of switch points, at another region in the wage frontier, with the perturbation of a model parameter. I am not totally happy with this example. The wage curves are often curved more sharply than is seen in real-world data. If I am going to look at a three-commodity example, I would like to find one where at least two wage curves intersect three times for positive, feasible rates of profits.
When I applied the terminology of co-dimension to patterns, I expected that it would be difficult to find, through numerical experimentation, examples of patterns of higher co-dimension. I expected I would have to consciously try to create them, as I did for this example of a global pattern. I argued at one point that patterns of co-dimension one are important for seeing how the sequence of switch points along the wage frontier can change with technical progress or changes in the strength of barriers to entry and so on. I am now leaning towards thinking this argument applies to at least some patterns of higher co-dimension.
Anyways, this example illustrates complications that can arise in price theory that I do not think have been previously noted.
2.0 TechnologyThe technology in this example is almost the same as in one of my previous examples. I modified one labor coefficient. The economy produces a single consumption good, called corn. Corn is also a capital good, that is, a produced commodity used in the production of other commodities. In fact, iron, steel, and corn are capital goods in this example. So three industries exist. One produces iron, another produces steel, and the last produces corn. Two processes exist in each industry for producing the output of that industry. Each process exhibits Constant Returns to Scale (CRS) and is characterized by coefficients of production. Coefficients of production (Table 1) specify the physical quantities of inputs required to produce a unit output in the specified industry. All processes require a year to complete, and the inputs of iron, steel, and corn are all consumed over the year in providing their services so as to yield output at the end of the year.
| Input | Iron Industry | Steel Industry | Corn Industry | |||
| a | b | c | d | e | f | |
| Labor | 1/3 | 1/10 | 5/2 | 7/20 | 1 | 3/2 |
| Iron | 1/6 | 2/5 | 1/200 | 1/100 | 1 | 0 |
| Steel | 1/200 | 1/400 | 1/4 | 3/10 | 0 | 1/4 |
| Corn | 1/300 | 1/300 | 1/300 | 0 | 0 | 0 |
A technique consists of a process in each industry. Table 2 specifies the eight techniques that can be formed from the processes specified by the technology. If you work through this example, you will find that to produce a net output of one bushel corn, inputs of iron, steel, and corn all need to be produced to reproduce the capital goods used up in producing that bushel.
| Technique | Processes |
| Alpha | a, c, e |
| Beta | a, c, f |
| Gamma | a, d, e |
| Delta | a, d, f |
| Epsilon | b, c, e |
| Zeta | b, c, f |
| Eta | b, d, e |
| Theta | b, d, f |
Each technique is represented by coefficients of production. For the Alpha technique, let a0, α be a three-element row vector representing the labor coefficients, and let Aα be the 3 x 3 Leontief matrix for this technique. The first element of a0, α, (1/3) person-years per ton, represents the labor input needed to produce a ton of iron. The first column of Aα represents the inputs of iron, steel, and corn needed to produce a ton of iron. A parallel notation is used for the other seven techniques.
3.0 The Price SystemPrices of production are defined to be constant spot prices that allow the smooth reproduction of the economy. Suppose Alpha is the cost-minimizing technique. Let p be the three-element row matrix designating the prices of iron, steel, and corn. I make the assumption that markets are such that the rate of profits in the iron, steel, and corn industries are (r s1), (r s2), and (r s3), respectively. Suppose S is a diagonal matrix with the obvious elements along the diagonal, and I designates the identity matrix. Then prices of production satisfy the following system of equations:
pα Aα (I + r S) + wα a0, α = pα
I choose a bushel of corn to be the numeraire. If e3 is the last column of the identity matrix, the following equation specifies the numeraire:
pα e3 = 1
As is not surprising, the above system of equations has one degree of freedom. One can solve for the wage, wα(r), as a function of the scale factor for the rate of profits, r. The is a downward-sloping curve that intercepts both the axis for the wage and the scale factor at positive values. A similar function can be derived the other techniques, and they can be graphed in the same diagram.
4.0 The Choice of TechniqueFigure 2 graphs the wage curves for all eight techniques, given specific values for the mark-ups, si, i = 1, 2, and 3. The outer envelope, called the wage frontier, represents the cost-minimizing technique for any given wage or scale factor for the rate of profits. (Although it is difficult to see in the graph, the Theta technique is cost-minimizing for a continuum of the wage between two switch points.) Notice that only two wage curves intersect at each switch point on the frontier. The techniques that are cost-minimizing at each switch point differ in only one process. This is a non-fluke example, for these markups. For what it is worth, the switch point between the Delta and Gamma techniques exhibits capital-reversing.
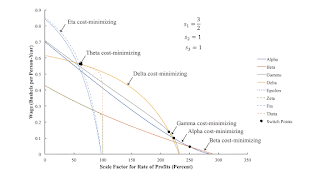
|
| Figure 2: The Wage Frontier Before a Four-Technique Pattern |
Table 3 shows the sequence of techniques that are cost-minimizing, along the wage frontier, at selected values of the markup for the iron industry. Figure 1, at the top of the post, illustrates the middle row. Presumably, two three-technique patterns have removed the Alpha and Gamma techniques from the frontier, for high values of the scale factor for the rate of profits. For the purposes of this post, I am not interested in those patterns. My point is focused on the switch point between the Eta and the Delta technique. Looking above at Table 2, one can see that, for these techniques, both processes in both the iron and corn industries are part of cost-minimizing techniques at the switch point. It follows that the Gamma and Theta techniques are cost-minimizing at this switch point, even though they do not appear on the wage frontier elsewhere. This is a fluke.
| s1 | s2 | s3 | Techniques |
| 3/2 | 1 | 1 | Eta, Theta, Delta, Gamma, Alpha, Beta |
| 2.665 | 1 | 1 | Eta, Delta, Beta |
| 4 | 1 | 1 | Eta, Gamma, Delta, Beta |
Finally, Figure 3 shows the wage frontier at the last level of the markup in the iron industry that I want to consider. The sequence of cost-minimizing techniques of Eta, Theta, and Delta, for relatively low scale factors for the rate of profits, has been replaced by the sequence of Eta, Gamma, and Delta. This example shows one sequence for how the wage frontier can be varied by lasting changes in a markup in one industry.

|
| Figure 3: The Wage Frontier After a Four-Technique Pattern |
5.0 Conclusion
Simple numerical examples are often presented in textbooks, such as Kurz and Salvadori's Theory of Production. They are often meant to illustrate phenomena that can appear in a more complicated example of a model. This post is an illustration of a fairly complicated example, where parts, in some sense, resemble simpler examples.



2 comments:
https://mpra.ub.uni-muenchen.de/84284/1/MPRA_paper_84284.pdf
Maybe It seems amusing for you.
Thanks. I am not sure your author fully takes into account that the measure of capital he proposes is dependent on prices, including the rate of profits. Sraffians have generally been skeptical that a measure of capital with these properties can satisfy the purposes of traditional neoclassical measurements. I'll have to read more to have a more adequate response.
I think the author will need to restructure this before he can publish it. He introduces equations before defining the symbols in them. He doesn't need so many examples. He needs more references. I can see writing a working paper with all these examples, though.
He could probably reference the Osborne and Davidson paper I argue about in my 2017 ROPE arcticle. They have a proposal for an average period of production. He might look through the references in my various gyrations in my anti-Austrian SSRN articles.
Post a Comment