An Example Of Fixed Capital From Salvatore Baldone

Figure 1: Wage Curves For A Technique In The Example

1.0 Introduction

I have explored this example from Baldone before, including perturbations of coefficients of production. My purpose here is to demonstrate that my Matlab code for Sraffian analysis can yield the correct results. (I have an off-by-one error that I hard-coded around in obtaining these graphs.)

My favorite method of analyzing the choice of technique applies to models of pure fixed capital. In such models, machines that last over multiple production periods are the only element of joint production. If a machine does not have constant efficiency over its physical life, the analysis of the choice of technique includes a decision on the economic life of the machine. The choice of technique can still be analyzed by the construction of the wage frontier as the outer envelope of wage curves. Unlike in single production, a wage curve can slope up off the frontier.

Baldone's numerical example illustrates an equivalent method for analyzing the economic life of a machine. It focuses attention on negative prices of old machines. The cost-minimizing technique is such that old machines are discarded, not operated. And it is an example of the reswitching of techniques.

2.0 Technology, Techniques, and Quantity Flows

Each column in Tables 1 and 2 defines a production process. Managers of firms know about each process. The first produces new machines, and the remaining three produce corn with machines of various vintages. For instance, a bushel corn and a one-year old machine are produced, in the second process, from inputs of 1/5 person-years of labor, 2/5 bushels corn, and one new machine.

Table 1: Inputs for The Technology

Input	Process
	(I)	(II)	(III)	(IV)
Labor	2/5	1/5	3/5	2/5
Corn	1/10	2/5	289/500	3/5
New Machines	0	1	0	0
One-Year Old Machines	0	0	1	0
Two-Year Old Machines	0	0	0	1

Table 2: Outputs for The Technology

Output	Process
	(I)	(II)	(III)	(IV)
Corn	0	1	1	1
New Machines	1	0	0	0
One-Year Old Machines	0	1	0	0
Two-Year Old Machines	0	0	1	0

I call Alpha the technique in which the machine is disposed of after one year and Beta the technique in which the machine is discarded after two years. In Gamma, the machine is run for its full three physical years

Suppose Alpha is adopted, and the first two processes are operated at a unit level. A new machine is simultaneously produced by the first process and operated to its economic life in the second. One bushel corn is produced. One half bushel is used to replace the corn input, leaving a net output of 1/2 bushel corn. This net output is produced by 3/5 person-years labor. Thus, Alpha requires 1.2 person-years per net bushel output ( = (3/5)/(1/2) = 6/5). I leave it for the reader that Gamma requires approximately 1.2103 person-years per net bushel corn, and that Beta requires approximately 1.3015 person-years per net-bushel produced.

3.0 Prices

In a vertically integrated firm, new and old machines are not sold on markets. Nevertheless, the accountants must enter prices on the books. The accounting I outline here can be used to derive the formula for an annuity if the efficiency of the machine were constant. However, since that is not the case, a general approach to depreciation is illustrated.

Let r be the interest rate, as given from the market, w the wage, p₀ the price of a new machine, p₁ the price of a one-year old machine, and p₂ the price of a two-year old machine. The interest rate is also known as the rate of profits. When the Gamma technique is operated, prices must satisfy the following system of four equations:

(1/10)(1 + r) + (2/5) w = p₀

((2/5) + p₀)(1 + r) + (1/5) w = 1 + p₁

((289/500) + p₁)(1 + r) + (3/5) w = 1 + p₂

((3/5) + p₂)(1 + r) + (2/5) w = 1

I take the wage as paid at the end of the year, and all prices are expressed in terms of the net product.

If the interest rate is given, the above system consists of four linear equations in four variables. It can be solved.

The price systems for the other two techniques are a subset of those. The price system for Beta, for instance, consists of the first three equations, with the price of a two-year old machine set to zero.

4.0 Non-Negative Prices and the Choice of Technique

"With decreasing or changing efficiency ... a problem of the choice of technique, that is, of the optimal truncation date, arises. Premature truncation is advantageous as soon as the price (book value) of a partly worn out instrument of production becomes negative. Since the price of a machine (either new or 'aged') is equal to the capital value one gets by discounting all future net recipts that may be obtained by further use of it, where the going rate of profit is taken as the discount rate, negative prices would indicte 'losses' and would thus contradict the assumption of a fully settled competitive position of the economy." -- Kurz and Salvadori (1995: 212).

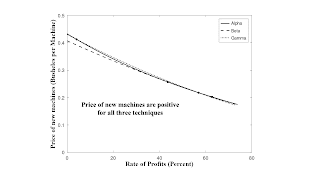
I can find when the price of each machine is positive. For new machines (Figure 2), their prices are positive:

• For Alpha, when 0 < r < 74.2 percent
• For Beta, when 0 < r < 73.8 percent
• For Gamma, when 0 < r < 72.7 percent.

The upper limits are approximate. The wage curves in Figure 1, at the top of this post, intersect the axis for the rate of profits at these upper limits.

Figure 2: Prices of New Machines

One-year old machines have positive prices (Figure 3):

• For Beta, when 43.6 percent < r < 62.7 percent
• For Gamma, when 4.1 percent < r < 56.9 percent

Under Alpha, the machine is discarded after one year, and the prices of old machines are identically zero. Beta is not operated outside the limits in which the price curve for Beta intersects the abscissa in Figure 3. If the machine were being truncated after two years, it would pay to discard it after one year. The same applies to Gamma. The analysis, so far, shows that Alpha would be adopted at the extremes of low and high rates of profits,

Figure 3: Prices of One-Year Old Machines

Two-year old machines have positive prices (Figure 4):

• For Gamma, when 0 < r < 55.7 percent

Since the price of a two year old machine is negative for rates of profits greater than at the switch point, Gamma will not be operated at those rates of profits.

Figure 4: Prices of Two-Year Old Machines

I can now summarize the analysis of the choice of technique for this example. Managers of firms will not adopt a technique when the outputs of a process in the technique has a negative price. Thus, each technique will be adopted in the following intervals:

• Alpha, for 0 < r < 4.1 percent and 62.7 percent < r < 74.2 percent
• Beta, for 55.7 percent < r < 62.7 percent
• Gamma, for 4.1 percent < r < 55.7 percent

Now, I can look at what happens around the three switch points:

• Around r = 62.7 percent, a lower interest rate is associated with a switch from Alpha to Beta, a more roundabout technique. But net output per worker falls. A more roundabout technique is less capital-intensive.
• Around r = 55.7 percent, a lower interest rate is associated with a switch from Beta to Gamma, a more roundabout technique. And net output per worker rises.
• Around r = 4.1 percent, a lower interest rate is associated with a switch from Gamma to Alpha, a less roundabout technique. And net output per worker rises. A less roundabout technique is more capital-intensive.

Only the middle switch point validates Austrian capital theory. Clearly, economists of the Austrian school have made mistakes in logic.

I like to note that the above argument is not about aggregation.

5.0 Conclusion

The above constitutes a proof that Austrian capital theory is mistaken. It relies on an identification, in the example, of more roundaboutness with a longer economic life of a machine. Austrian economists have tried to express their central insight that a greater use of capital is equivalent to a greater use of time in several disparate ways.

Perhaps greater roundaboutness should be identified with the use of different, better machines. By putting aside some time each day, Crusoe can make a net, instead of relying on whatever lies about at hand when catching fish. Or perhaps roundaboutness should be measured by a average period of production. Or by a financial measure of duration. What about those Hayekian triangles?

Since the central insight happens to be wrong, each of these formulations can be demonstrated to be, at best, ad hoc. But for each formulation, to be shown wrong in detail, requires a separate argument. Such can be provided and has been provided for most. Both Austrians and more mainstream marginalists have been in the position, for decades, that every economist is their own capital-theorist.

References

• Baldone, Salvatore (1974), Il capitale fisso nello schema teorico di Piero Sraffa, Studi Economici, XXIV(1): 45-106. Trans. in Pasinetti (1980).
• Kurz, Heinz D. and Neri Salvadori. 1995. Theory of Production: A Long-Period Analysis. Cambridge: Cambridge University Press.
• Pasinetti, Luigi L., (1980) (ed.), Essays on the Theory of Joint Production, New York: Columbia University Press