|
| Figure 1: The Choice of Technique in a Model with One Commodity |
This post presents a reswitching example in a one-good model. The single produced commodity in the example can be used as both a consumption and a capital good. It is produced by expenditure of labor with its services. It lasts for three production periods, and its technical efficiency varies over the course of its lifetime, when used as a capital good.
I do not remember any comparable numeric example in the literature. If I recall Ian Steedman's 1994 article, he gives instructions for constructing a one-good example, but does not present one. Maybe if I reread it now, I will find it clearer. I have previously worked through a reswitching example, with fixed capital, from J. E. Woods. But that is a multi-commodity model. I have also once echoed Sraffa's analysis of depreciation charges, in a case with constant efficiency.
2.0 TechnologyThis is an example of fixed capital, a kind of joint production. Three production processes are known by the manager of firms, and they each exhibit constant returns to scale. Each process requires a year to complete, and each process produces new widgets. Table 1 shows the inputs for each process, when operated at a unit level, and Table 2 shows the outputs. For example, process I requires inputs of labor and new widgets. The outputs of process I consist of new widgets and the widgets which provided their services throughout the year it is under operation. Those leftover widgets are one year older, though. Consumers consume new widgets during the year following on their purchase. The physical life of widgets, when providing services for production, is three years. Thus, three processes can be operated in production.
| Input | Process | ||
| (I) | (II) | (III) | |
| Labor | 10 | 60 | 13/2 |
| New Widgets | 1/3 | 0 | 0 |
| One-Year Old Widgets | 0 | 1/3 | 0 |
| Two-Year Old Widgets | 0 | 0 | 1/3 |
| Output | Process | ||
| (I) | (II) | (III) | |
| New Widgets | 1 | 7/12 | 79/20 |
| One-Year Old Widgets | 1/3 | 0 | 0 |
| Two-Year Old Widgets | 0 | 1/3 | 0 |
Firms are not required to operate all three processes. They can truncate the use of widgets after one or two years. Assume free disposal, that is, that discarding widgets does not incur a cost. Under these assumptions, three techniques are available to produce new widgets, as shown in Table 3.
| Technique | Processes |
| Alpha | I |
| Beta | I, II |
| Gamma | I, II, II |
3.0 Price Equations
Managers of widget-producing firms choose the technique, that is, the truncation period, on the basis of cost. As usual, consider a competitive economy, in which workers and firms are free to seek out higher wages and profits, respectively. Revenues and costs are calculated on the basis of a set of prices in which workers and firms have no incentive to move out of one process and into another. Workers receive a common wage of w new widgets per person-year. Assume workers are paid out of the surplus at the end of each year. Firms receive a rate of profits of 100 r percent in operating each process in use. For notational convenience, define R:
R = 1 + r
Let p1 be the price of a one-year old widget and p2 the price of a two-year old widget.
I confine the systems of price equations for the Alpha and Beta techniques to an appendix. Accordingly, assume the Gamma technique is in use. The wage, prices, and the rate of profits must satisfy a system of three equations:
(1/3)R + 10 w = 1 + (1/3) p1
(1/3) p1 R + 60 w = 7/12 + (1/3) p2
(1/3) p2 R + (13/2) w = 79/20
Given the rate of profits below some maximum, one can solve for the wage:
wγ = (60 R2 + 35 R + 237 - 20 R3)/(10 (60 R2 + 360 R + 39))
The price of two-year old and one-year old widgets fall out:
p2, γ = (237 - 390 wγ)/(20 R)
p1, γ = (7 + 4 p2, γ - 720 wγ)/(4 R)
If you feel like it, you can substitute on the Right Hand Sides of the above two equations so as to express prices as functions exclusively of the rate of profits.
4.0 Choice of TechniqueI have explained above how to find the wage, as a function of the rate of profits, when the Gamma technique is in use. The wage-rate of profits curves for the Alpha and Beta technique are, respectively:
wα = (3 - R)/30
wβ = (12 R + 7 - 4 R2)/(120 (R + 6))
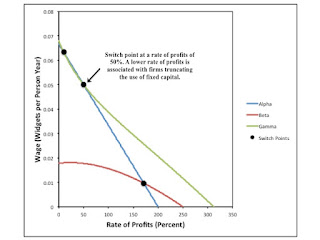
Figure 1 graphs all three wage curves. The cost-minimizing technique, at any given rate of profits, is the technique on the outer envelope of the wage curves. The switch points between the Alpha and Gamma techniques are at rates of profits of 10% and 50%. Below 10% and above 50%, the Gamma technique is cost-minimizing. Widgets are used in production processes to the extent of their physical life. Between these rate of profits, the Alpha technique is cost minimizing. The use of widgets, as capital goods, is truncated after one year. For what it is worth, the switch point between the Alpha and Beta techniques, within the outer envelope, is at a rate of profits of 41/24, approximately 171%.
4.1 A Direct Method with Alpha PricesIn the general theory of joint production, an analysis of the choice of technique cannot generally be based on wage-rate of profits curves. Such an analysis does work in this model of fixed capital. But I checked it with a more direct method of analysis.
Suppose the Alpha technique is in use. The prices of one-year old and two-year old widgets are zero. The wage is as found from the system of price equations associated with the Alpha technique. Would it pay to produce new widgets with one-year old or two-year old widgets? Figure 2 shows calculations to determine if supernormal profits can be earned with the Beta or Gamma technique.

|
| Figure 2: Supernormal Profits at Alpha Prices |
Since the Alpha technique is in use, its net present value is zero. Extra profits are assumed to have been competed away.
If the Beta technique is operated, no extra profits or losses are earned in operating process I under the Beta technique. In operating process II, the services of old widgets are free, and no revenues are received for the two-year old widgets disposed of at the end of the year. At low rates of profits and high wages, the revenues received for new widgets produced with process II do not cover labor costs. At high rates of profits, the opposite is the case. These prices, when wages are low, signal to firms that they can earn extra profits by extending the truncation period one year.
The analysis for the Gamma technique is more cumbersome. Firms can not adopt process III without also operating process II. Accordingly, the net present value for the Gamma technique is found by accumulating all costs and revenues for all three processes to the end of the third year. In such a weighted sum, the revenues for process I are multiplied by (1 + r)2, and the revenues for process II are multiplied by (1 + r). At a rate of profits below 10% and above 50%, firms will want to adopt the Gamma technique and produce with old widgets to the end of their physical life.
4.2 A Direct Method with Beta PricesI find of interest some complications that arise in applying this direct method with wages and prices, as calculated for the Beta price system. Figure 3 shows the net present value for the processes comprising each of the three techniques. At all rates of profits, these prices signal that firms should extend the truncation period, from two years, to the three years specified by the Gamma technique. This is so, even for rates of profits between 10% and 50%. If firms start at a two-year truncation period, they will only find that they need to truncate to one year after first extending production to three years. (See A.3 in the Appendix for graphs associated with the Gamma price system.)

|
| Figure 3: Supernormal Profits at Beta Prices |
When the Beta technique is operated, a price must be assigned to the price of a one-year old widget. In the theory of joint production, prices can be negative when calculated for rates of profits below the maximum. (This is not so for pure circular capital models without joint production.) Figure 4 graphs the price of one-year old widgets, under the system of prices associated with the Beta technique. This price is negative for rates of profits of approximately 171%. Confine your attention to the Alpha and Beta techniques for a second. The negative price of one-year old widgets signals firms that it is profitable to truncate production from two years to one year.

|
| Figure 4: Price of One-Year Widget with Beta Technique |
The application of a direct method for comparing costs and revenues for techniques of production confirms, in the context of this model of fixed capital, the results of constructing the outer envelope curve from the wage-rate of profits curves for the techniques.
5.0 ConclusionThe literature on macroeconomics contains many models with aggregate production functions and in which the one produced commodity can be either consumed by households or used as a capital good in further production. And, in many of these models, this capital good depreciates over many periods. These models are one-good models, in the sense of this post. Some mainstream economists ignorantly assert that the Cambridge Capital Controversy was exclusively about problems in aggregating capital goods. Since mainstream economists are aware of aggregation issues, they somehow conclude they are justified in ignoring the controversy. I usually refute this rot by pointing out consequences for microeconomics of the analysis of the choice of technique. This post takes an alternative approach. It examines a highly aggregated model. And issues related to Sraffa effects arise in the one-good model, too.
This example also has a bearing on a misunderstanding common among the Austrian school of economics. Böhm Bawerk, at least, thought of production processes taking a longer amount of time as being more capital intensive and, therefore, more productive, in some sense. Firms are supposedly restricted in how willing they are to temporally extend production processes because of the scarcity of capital, as reflected in the interest rate. If households were less impatient and more willing to save, the interest rate would fall and firms would adopt longer processes. One can find many Austrian school economists (for example, Hayek in the 1930s) rejecting the idea that there exists a meaningful quantitative measure of roundaboutness or the period of production, whether independent of prices or not. But Austrian school economists generally retain a sense that the theory is insightful and somehow qualitatively true. The numeric example challenges this idea. One would think that a truncation of the production process, with the capital good not reaching its physical lifetime, is unambiguously less roundabout. As noted in Figure 1, for one switch point in the example, such a truncation can be associated with a lower interest rate.
Appendix AI confine various mathematical details to this appendix.
A.1 Alpha Price EquationsIf the Alpha technique is in use, the prices of one-year old and two-year old widgets is zero:
p1, α = p2, α = 0The wage and the rate of profits are related by the coefficients of production for process I:
(1/3)R + 10 w = 1
The wage, under the Alpha technique, can be expressed as a function of the rate of profits, as illustrated in Figure 1.
A.2 Beta Price EquationsIf the Beta technique is in use, the price two-year old widgets is zero:
p2, β = 0
A system of two equations arises for the Beta technique:
(1/3)R + 10 w = 1 + (1/3) p1
(1/3) p1 R + 60 w = 7/12
The wage as a function of the rate of profits, for the Beta technique, is also illustrated above. The price of one-year old widgets is:
p1, β = R + 30 wβ - 3A.3 Direct Method with Gamma Prices
This section presents two graphs with wages and the rate of profits found from the system of prices for the Gamma technique. Figure 5 shows the net present value of truncating the use of widgets after one, two, or three years. For all techniques, revenues and costs are accumulated, at the going rate of profits to the end of the last year in which widgets are produced with the technique. The net present value for operating the Alpha technique (truncating after one year) is positive between the switch points at rates of profits of 10% and 50%.

|
| Figure 5: Supernormal Profits at Gamma Prices |
Figure 6 shows the prices of one-year old and two-year old widgets for the solution to the Gamma price system. Although not very easy to see in the graph, the price of one-year old widgets is negative at rates of profits between 10% and 50%.

|
| Figure 6: Price of Widgets with Gamma Technique |
References
- Ian Steedman. 1994. 'Perverse' Behaviour in a 'One Commodity' Model. Cambridge Journal of Economics, V. 18, No. 3: pp. 299-311.



6 comments:
That's quite interesting. My superficial impression then is that more than one capital commodities is not necessary to generate "kinks" in the aggregate "production function", it is sufficient to have just different processes for that one capital good with different schedules, instead of different processes for different capital goods. I guess that means that to handwave that away neoclassical economists will just assume suitably well behaved frontier/outer envelopes.
In further wicksellian news, Brad DeLong has recently vehemently objected to the notion of the one true "natural rate of interest" because a 20 year old paper showed that it can't be estimated:
www.bradford-delong.com/2016/12/must-read-i-do-not-get-this-it-was-21-years-ago-that-i-learned-from-an-early-draft-of-staiger-stock-and-watson-199.html
«it was 21 years ago that I learned--from an early draft of Staiger, Stock, and Watson (1997)--that nobody had any business thinking or acting on any belief that they had the correct estimate of the natural rate. The natural rate shifts. And because the natural rate shifts there is no way to estimate it precisely, even in retrospect, let along in prospect»
It surprises me somewhat that a paper is needed to establish that a hand-waving metaphysical concept is not that useful to understand political economies; it does not surprise me though that vigorous debate on the true level of the natural rate of interest continues, and I wonder how many PhD dissertations have had, in the past 20 years, titles like "Towards an improve method for estimating the natural rate of interest". :-)
As to the continuing vigorous debate on the true level of the natural rate of interest, an article from "The Economist" quoting Brad DeLong dated 2013:
www.economist.com/blogs/freeexchange/2013/10/are-real-rates-too-high-or-too-low
Thanks. For what it is worth, here is Delong's comment as a link. And here is the Economist link.
Colin Rogers is good to read on why the results of the Cambridge Capital Controversy invalidates Wicksell's theory of the natural rate. Gunnar Myrdal had a Keynes-like, internal critique of Wicksell in his book Monetary Equilibrium.
Can't stay away from this blog... :-)
I have just remember this excellent summary by Joan Robinson of (some of) the troubles with the handwaving on production, amply quoted by the erudite "Sandwichman":
http://econospeak.blogspot.co.uk/2016/09/nine-spades-are-lump-of-leets.html
«In long-period analysis, the neo-neoclassics are prone to confuse a comparison of positions of equilibrium (as in a pseudo-production function) with a "Wicksell process" of accumulation without technical progress. "A given state of technical knowledge" consists simply of a production function in terms of leets and labour. Accumulation consists of adding some leets to the pre-existing stock and squeezing it into a new quantity per man employed. This entails raising the wage rate and reducing the return per ton of leets. Thus a process of raising the capital-labour ratio means creeping along the production function, moving step by step from lower to higher ratios of leets to labour. (It is notable that when Professor Samuelson conceded defeat in the "reswitching" controversy, he did so in this form. He seemed to suppose that if the process of accumulation hit a backward switch, where a lower rate of profit is associated with a lower value of capital per man, the economy would suddenly find itself able to consume part of its capital without reducing its productive capacity.)»
And "Sandwidchman" also quotes from a Stanley Bober:
«The neoclassical explanation of the distribution of income is based on [ ... ] the demand for the resource being derived ultimately from its contribution to output at the margin, [ ... ] Now Sraffa was able to show that a system of equilibrium prices could be derived independently of any notion of marginal change and without any direct relation to the role played by the demand for factor services. There was simply no need to rely on the ideas of marginal disutility or marginal productivity to determine equilibrium prices.»
Hi Robert, in this book there is a chapter by Ian Steedman (Ch 5) where the same topic is treated.
https://books.google.es/books?id=Z8esAgAAQBAJ&pg=PA217&lpg=PA217&dq=caspari+schefold&source=bl&ots=s7ypccXcHC&sig=XkVyuNEG6HA9BqnBrQspM2dGbTM&hl=es&sa=X&ved=0ahUKEwjB8MKL1q3RAhVHPBQKHfrhAuwQ6AEIKjAC#v=onepage&q=caspari%20schefold&f=false
I don't know if at the end it is just the same paper specially selected for the Contribution to Schefold.
Feliz 17
Feliz, thanks. I thought I might have had a two or three page paper.
Post a Comment