What is held constant when defining the marginal product of labor? A correct answer, in the context of a neoclassical long period theory, is the interest rate. This is part of the answer Paul Samuelson gave to Joan Robinson in the early 1960s when she visited MIT. My exposition of this answer is indebted to an explanation of Frank Hahn's.
2.0 The Model Economy
Consider an economy that produces wheat and corn in yearly production cycles. At the start of the year, a firm producing wheat buys inputs of labor, corn, and wheat. The production process takes a year. The firm's output of wheat is available at the end of the year. Likewise, a firm buying corn purchases inputs of labor, corn, and wheat at the start of the year and has outputs of corn at the end of the year.
In neoclassical theory, goods are differentiated by their availability at different times. So there will be five prices to consider for a yearly production cycle:
- w, the wage, which I arbitrarily assume here is paid at the beginning of the year.
- P(1) = (p11, p21), the row vector of spot prices of wheat and corn for immediate delivery at the beginning of the year.
- P(2) = (p12, p22), the vector of forward prices of wheat and corn for delivery at the end of the year. For example, p12 is the price that must be paid at the start of the year for a contract in which the buyer will receive a bushel of wheat at the end of the year.
Now consider a competitive firm producing wheat. Assume the firm faces a constant returns to scale production function:
(1)
where Q1 is the output of bushels wheat, L01 is inputs of labor, X11 is inputs of wheat, and X21 is inputs of corn. Since I assume Constant Returns to Scale, I can separate questions of scale and relative proportions:
(2)
where
(3)
(4)
(5)
I make the usual assumption that diminishing marginal returns exist for each input in both production functions.
In the next part, I derive the marginal productivity equations for a competitive wheat-producing firms.


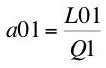





No comments:
Post a Comment