Consider a very simple capitalist economy in which the value of all net output is distributed as wages or (accounting) profits:
where Y is net output, W is total wages, and P is total profits. The term "profits" is used in some economic traditions to mean what some neoclassical economists call "interest". If this causes confusions, read "profit" as "interest" throughout this essay, except where "economic profit" is used.(1)
If there is some homogeneous unit in which to measure the labor force (person-years), the wage w is related to total wages as in Equation 2:
where L is the number of person-years employed. Similarly, if the capital K used up in a year can be valued in the same units as output, total profits relate to the interest rate r as in Equation 3:(2)
Equations 1, 2, and 3 are accounting identities, true by definition. No assumptions have been made yet about how any of these variables are determined.(3)
Continuing with the manipulation of accounting identities, one can transform Equation 1 to Equation 4:
Or:(4)
where y is net output per head and k is the value of capital per head. Note that the value of output per head, the wage, and the value of capital per head are all measured in the same units, say bushels of wheat. The interest rate is a percentage rate with no units attached (other than, perhaps, an implicit time dimension).(5)
Some neoclassical economists relate net output to inputs of labor and capital by means of an aggregate production function, which, when written in per capita form looks like Equation 6:
The function f is supposed to satisfy certain assumptions that characterize Constant Returns to Scale and diminishing marginal returns to each factor. Given these assumptions and perfect competition, cost minimization (or the maximization of economic profit) is supposed to ensure the equilibrium conditions given by Equations 7 and 8:(6)
(7)
Equation 7 shows the interest rate is equal to the marginal product of capital, while Equation 8 shows an equality between the wage and the marginal product of labor [3]. I intend to challenge Equation 7 in a framework that includes Equations 5, 6, 7, and 8.(8)
The argument for the aggregate production function, when written in per capita form, is the value of capital per head. How can the value of capital per head vary? Consider a multi-commodity model in a steady state. Suppose the same technique is adopted at different interest rates. The corresponding price structure will vary with the interest rate. Even though the same capital goods may be used at different interest rates, the value of capital per head will differ with the interest rate. This variation in the value of a given set of capital goods with the interest rate is known as a price Wicksell effect.
Typically, though, the cost-minimizing technique will also vary with the interest rate. Consider the prices ruling at a given interest rate, where that interest rate is a switch point. That is, at least two techniques are cost minimizing at the given interest rate. We can then consider variations in capital goods resulting from a variation in the usage of two cost minimizing techniques. The resulting variation in the value of capital per head at the given prices is known as a real Wicksell effect. The chain-rule for differentiation shows how the price and real Wicksell effects combine to determine the total variation in the value of capital per head with the interest rate [4].
For completeness, I note there is a third manner in which the value of capital per head can vary, namely if the composition of final output varies, for example, due to a difference in the rate of growth. This possibility is not important to my argument.
Now I want to prove a theorem by some simple formal manipulations. Given Equation 5, the marginal product of capital is equal to the interest rate (Equation 7) if and only if Equation 9 holds [5]:
(9)
Proof: Equation 10 gives the total differential of both sides of Equation 5:
Thus, the interest rate is equal to the marginal product of capital (Equation 7) if and only if Equation 11 holds:(10)
Equation 9 follows. Q.E.D.(11)
A demonstration that the value of capital per head need not be equal to the additive inverse of the slope of the factor price frontier (Equation 9) demonstrates that the interest rate need not be equal to the marginal product of capital (Equation 7).
Footnotes
[3] A more general statement of these relations, abstracting from price Wicksell effects, is given by Equations 7' and 8' in terms of left-hand and right-hand derivatives:
(7')
In the discrete case without price Wicksell effects, the neoclassical aggregate production function is supposed to resemble the function in Figure 1.(8')
 |
| Figure 1: Interest Rate Bounded By Marginal Products |
[4] A good explanation of price and real Wicksell effects can be found in:
- Edwin Burmeister, "Wicksell Effects," The New Palgrave.
"The value of capital, however, is not an appropriate measure of the 'aggregate capital stock' as a factor of production except under extremely restrictive assumptions. Wicksell (1893, 1934) originally recognized this fact, which subsequently was emphasized by Robinson (1956)."
[5] Equation 9 follows from Equation 7' at a non-switching point in the discrete case. Consider a second set of values of y, w, r, and k, related as in Equation 5:
The difference between these two sets of values is given by Equation II:(I)
Or, in obvious notation:(II)
Assume Equation 7' holds. Two cases arise.(III)
Case 1:
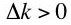 . By diminishing marginal productivity, one also has
. By diminishing marginal productivity, one also has 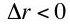 . Ignoring higher order terms, the production function is:
. Ignoring higher order terms, the production function is:From Equation 7', one has:(IV)
Or:(V)
Substitute from Equation III:(VI)
A little algebra yields:(VII)
Take the limit as the value of capital per head approaches k from above (and therefore the interest rate approaches r from below):(VIII)
(IX)
Case 2:
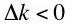 and thus
and thus 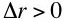 Ignoring higher order terms, one has:
Ignoring higher order terms, one has:The inequality in Display V follows, once again, from Display 7'. An argument parallel to the first case yields the inequality in Display XI:(X)
The left-hand and right-hand derivatives of the factor-price frontier are equal at a non-switching point in the discrete case. The two cases establish that that derivative is equal to the value of capital per head:(XI)
which was to be shown.(XII)
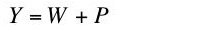

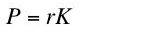

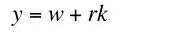
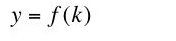
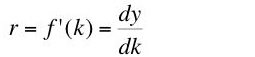
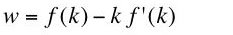
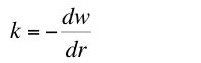






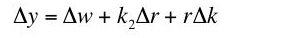

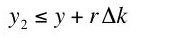

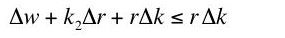

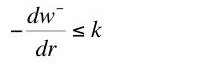


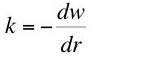



No comments:
Post a Comment