Proof Of The Falsity Of The Factor Price Equalization "Theorem" (Part 2)

3.0 Prices And The Choice Of Technique
In the previous part, I presented a specification of the technology in a numeric example created by Lynn Mainwaring. Which technique specified by this technology is cost minimizing at equilibrium prices? In this context, equilibria have the following properties:

• The iron-producing process, at least one steel-producing process, and at least one corn-producing process are operated.
• The costs of inputs for each process in operation does not exceed revenues.
• No process can be used to obtain pure economic profits.

Suppose, for example, that the Alpha technique is cost minimizing. Given these properties, then the following equations must be satisfied:

(1/5) p2 (1 + r) + (1/20) w = p1

[(1/5) p1 + (1/10)](1 + r) + (1/5) w = p2

[(1/10) p1 + (1/2) p2](1 + r) + (9/20) w = 1

where

• w is the wage (in units of bushels per person-year)
• r is the rate of profits
• p1 is the price of iron (in units of bushels per ton iron)
• p2 is the price of steel (in units of bushels per ton steel)

The above equations specify that, for each process in the Alpha technique, costs of inputs in the process equal revenues. The costs do not exceed revenues. Furthermore, no process, at least in the Alpha technique, can be operated to obtain pure economic process.

Suppose, for mathematical convenience, the rate of profits is externally specified. Then the above is a system of three linear equations in three variables. It can be solved, and the solution is:

w = 2 [500 - 45(1 + r)^2 - (1 + r)^3]/[450 + 105(1 + r) - 9 (1 + r)^2]

p1 = (1/2) [100 + 80(1 + r) + 13(1 + r)^2]/[450 + 105(1 + r) - 9(1 + r)^2]

p2 = (1/2)[400 + 110(1 + r) + (1 + r)^2]/[450 + 105(1 + r) - 9(1 + r)^2]

A system of equations is associated each of the remaining three techniques defined by the technology. The statement of those systems and their solutions is relegated to an appendix. The cost minimizing technique at any given rate of profits can be found from these solutions. In particular, Figure 3-1 shows a graph of the wage as a function of the rate of profits for each technique. The cost minimizing technique at a given rate of profits is the technique for which the wage is greatest. The figure shows the frontier defined by this criteria as a heavy black line. The Delta technique is cost minimizing at low rates of profits. The Beta technique is cost minimizing at intermediate rates of profits, and the Alpha technique is cost minimizing at intermediate rates of profits.

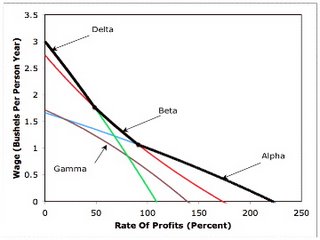Figure 3-1: The Wage-Rate Of Profits Frontier

But what does all of this have to do with the theory of international trade? This question will be answered in the next part.

Appendix 3.A: Price Equations For Three Techniques
Appendix 3.A.1: The Beta Technique
The price equations for the Beta technique are:

(1/5) p2 (1 + r) + (1/20) w = p1

[(1/5) p1 + (1/10)](1 + r) + (1/5) w = p2

(43/25) p1 (1 + r) + (19/100) w = 1

The solution to the Beta price equations is:

w = (2)[1,250 - 50(1 + r)^2 - 43(1 + r)^3]/[153(1 + r)^2 + 215(1 + r) + 475]

p1 = (1/2)[19(1 + r)^2 + 200(1 + r) + 250]/[153(1 + r)^2 + 215(1 + r) + 475]

p2 = (1/2)[43(1 + r)^2 + 145(1 + r) + 1,000]/[153(1 + r)^2 + 215(1 + r) + 475]

Appendix 3.A.2: The Gamma Technique

(1/5) p2 (1 + r) + (1/20) w = p1

(8/25)(1 + r) + (3/50) w = p2

[(1/10) p1 + (1/2) p2](1 + r) + (9/20) w = 1

The solution to the Gamma price equations is:

w = 8[625 - 100(1 + r)^2 - 4(1 + r)^3]/[6(1 + r)^2 + 175(1 + r) + 2,250]

p1 = 2[52(1 + r)^2 + 30(1 + r) + 125]/[6(1 + r)^2 + 175(1 + r) + 2,250]

p2 = 4 [2(1 + r)^2 + 180(1 + r) + 75]/[6(1 + r)^2 + 175(1 + r) + 2,250]

Appendix 3.A.3: The Delta Technique
The price equations for the Delta technique are:

(1/5) p2 (1 + r) + (1/20) w = p1

(8/25)(1 + r) + (3/50) w = p2

(43/25) p1 (1 + r) + (19/100) w = 1

The solution to the Delta price equations is:

w = 4 [3,125 - 344(1 + r)^3]/[258(1 + r)^2 + 1,075(1 + r) + 2,375]

p1 = [152(1 + r)^2 + 150(1 + r) + 625]/[258(1 + r)^2 + 1,075(1 + r) + 2,375]

p2 = [344(1 + r)^2 + 760(1 + r) + 750]/[258(1 + r)^2 + 1,075(1 + r) + 2,375]

Proof Of The Falsity Of The Factor Price Equalization "Theorem" (Part 1)

1.0 Introduction
This sequence of posts explores a numeric example. The example was created by L. Mainwaring (1976). Mainwaring used the example to prove the factor price equalization theorem to be false. Before explaining this implication of the example, I want to consider a single country.

2.0 Technology
Consider a simple economy in which three commodities, iron, steel, and corn, are produced from inputs of labor, iron, steel, and corn. All production processes in in this example require a year to complete and exhibit Constant Returns to Scale. One process is known for producing iron, and two processes each are known for producing steel and corn. These processes are shown in Table 2-1. The inputs for each process are purchased at the beginning of year. The inputs provide their services over the course of the year, and the iron, steel, and corn inputs are totally used up each year in the production processes. The outputs become available at the end of the year.

Table 2-1: Technology

INPUTS HIRED AT START OF YEAR	IRON- PRODUCING PROCESS (A)	FIRST STEEL- PRODUCING PROCESS (B)	SECOND STEEL- PRODUCING PROCESS (C)	FIRST CORN- PRODUCING PROCESS (D)	SECOND CORN- PRODUCING PROCESS (E)
Labor	1/20 Person-Year	1/5 Person-Year	3/50 Person-Year	9/20 Person-Year	19/100 Person-Year
Iron	0 Ton Iron	1/5 Ton Iron	0 Ton Iron	1/10 Ton Iron	1 18/25 Tons Iron
Steel	1/5 Ton Steel	0 Ton Steel	0 Ton Steel	1/2 Ton Steel	0 Ton Steel
Corn	0 Bushel Corn	1/10 Bushel Corn	8/25 Bushel Corn	0 Bushel Corn	0 Bushel Corn
OUTPUT	1 Ton Iron	1 Ton Steel	1 Ton Steel	1 Bushel Corn	1 Bushel Corn

A technique consists of three processes, where one process is used to produce iron, a second process produces steel, and the third process produces corn. As shown in Table 2-2, three techniques are available in this economy. Note that for each technique, no commodity can be produced without inputs either directly or indirectly of each other commodity For example, consider the Delta technique. Since corn is produced in this technique with process E, iron is required to be reproduced for production to continue year after year. Steel is required to reproduce iron by process A in this technique. And corn is required to produce steel by process C. In the jargon, iron, steel, and corn are all said to be “basic commodities”. Sraffa invented this terminology.

Table 2-2: Techniques And Processes

Technique	Processes
Alpha	A, B, D
Beta	A, B, E
Gamma	A, C, D
Delta	A, C, E

I leave as an exercise for the reader to check that, for each technique, some level of operation of the processes comprising the technique results in a positive net output. That is, after replacing the commodities used up in production, some output is left over to be used for consumption or accumulation. One method of checking this condition is to confirm the Hawkins-Simon conditions are met for each technique.

Consider cost-minimizing (or profit-maximizing) competitive firms facing this technology. Suppose that, although labor is hired at the start of the year, the workers are paid their wages at the end of the year. Iron, steel, and corn inputs are paid for at the beginning of the year, and interest (or profit) is charged on these payments. For each level of the rate of profits, which technique is cost minimizing? Is one technique not cost-minimizing at any rate of profits? I answer these questions in the next part by presenting the results of some tedious algebra.

References

• Mainwaring, L. (1976). "Relative Prices and 'Factor Price' Equalisation in a Heterogeneous Capital Goods Model", Australian Economic Papers, Republished in Fundamental Issues in Trade Theory (Ed. by Ian Steedman), Macmillan, 1979.

Vacation Versus Pressure To Blog

I've seen that once I started this blog, I feel pressure to post. But as is obvious, I don't post often. It would only be polite to respond to comments. But as long as an actual discussion is going on in the comments to a post, I can get away with saying nothing. I'm fairly slow to respond to e-mail too.

I will be even more intermittent in the next few weeks. I'm taking a vacation next week, and I am thinking of taking a few days off in the week after next. So I won't be posting then.

Lawrence Lessig Has A Blog

Lawrence Lessig is a lawyer and law professor in the United States. He is most well known, I guess, for his interest in intellectual property law. I take it that he is aware that property rights are shaped and defined by a plethora of laws and customs. I think he thinks that these laws should be judged instrumentally. So I think his views exhibit a family resemblance to those of Dean Baker and those pointed out on this blog in this series of posts.

Gramsci Quote, At Least Some Recited At Sraffa's Funeral

I know, from reading Geoff Harcourt, that at least some of this was quoted at Sraffa's funeral:

"It would be worth compiling a 'reasoned' catalogue of the men of learning whose opinions are widely quoted or contested in the book, each name to be accompanied by notes on their significance and scientific importance (this to be done also for the supporters of the philosophy of praxis who are certainly not quoted in the light of their originality and significance). In fact there are only the most passing references to the great intellectuals. The question is raised: would it not have been better to have referred only to the major intellectuals on the enemy side, leaving aside the men in the second rank, the regurgitators of second-hand phrases? One gets the impression that the author wants to combat only the weakest of their positions (or the ones which the weakest adversaries have maintained least adequately), in order to obtain facile verbal victories - for one can hardly speak of real victories. The illusion is created that there exists some kind of more than formal and metaphorical resemblance between an ideological and a politico-military front. In the political and military struggle it can be correct tactics to break through at the points of least resistance in order to be able to assault the strongest point with maximum forces that have been precisely made available by the elimination of the weaker auxiliaries. Political and military victories, within certain limits, have a permanent and universal value and the strategic end can be attained decisively with a general effect for everyone. On the ideological front, however, the defeat of the auxiliaries and the minor hangers-on is of all but negligible importance. Here it is necessary to engage battle with the most eminent of one's adversaries. Otherwise one confuses newspapers with books, and petty daily polemic with scientific work. The lesser figures must be abandoned to the infinite casebook of newspaper polemic.

A new science proves its efficacy and vitality when it demonstrates that it is capable of confronting the great champions of the tendencies opposed to it and when it either resolves by its own means the vital questions which they have posed or demonstrates, in peremptory fashion, that these questions are false problems.

It is true that an historical epoch and a given society are characterised rather by the average run of intellectuals, and therefore by the more mediocre. But widespread, mass ideology must be distinguished from the scientific works and the great philosophical syntheses which are its real cornerstones. It is the latter which must be overcome, either negatively, by demonstrating that they are without foundation, or positively, by opposing to them philosophical syntheses of greater importance and significance. Reading the Manual one has the impression of someone who cannot sleep for the moonlight and who struggles to massacre the fireflies in the belief that by so doing he will make the brightness lessen or disappear." (Gramsci 1971, pp. 432-433, "Critical Notes on an Attempt at Popular Sociology")

(The attempt being considered here is The Theory of Historical Materialism: A Manual of Popular Sociology, a book by Nikolai Bukharin.)

References

• Harcourt, G. C. (1986). "On the Contributions of Joan Robinson and Piero Sraffa to Economic Theory", in Controversies in Political Economy: Selected Essays, New York University Press
• Gramsci, Antonio (1971). Selections from the Prison Notebooks of Anonio Gramsci (Trans. by Quintin Hoare and Geoffrey Nowell Smith), International Publishers.

Daily Kos Diarist Discovers My Existence

Shattering 'Market Theory'

Programs For Post-Capitalist Society

This is a topic that I could see myself exploring some time in the distant future.

The author of an utopia is promoting his vision in some virtual place that I sometimes read. I only glanced at this page, but I could not quickly find any discussion of competing programs. I think the most serious such programs around these days are:

• Michael Albert and Robin Hahnel's participatory economics
• W. Paul Cockshott and Allin Cottrell's Towards A New Socialism

More On The Incorrect Heckscher-Ohlin-Samuelson (HOS) Theory

I have some comments in "Unregulated International Trade Unjustified By Comparative Advantage (TOC)". Radek offers an admittably speculative explanation of why there is a loss from trade in my numeric example:

"Increasing returns isn't the correct term. Nonconvex production set is what I'm guessing."

I think that explanation is wrong. I pointed out in the comments that the numeric example is not a reswitching example. Radek comments on this observation:

"I think Metcalfe and Steedman emphasized reswitching as necessary for this kind of result then later folks realized that reswitching wasn't it. But like I said, I'm not too familiar and it's been awhile.

Ok - I think I found the MS article and will read up on it (JIL May'77)."

The phrase "this kind of result" is doing too much work here. As I mentioned, Metcalfe, Steedman, and others have a variety of criticisms of the logic of HOS theory. The criticism illustrated by my example is from Metcalfe and Steedman (1974). Steedman and Metcalfe (1977) is a different criticism, a criticism that stretches my knowledge of trade theory by the by. They conclude:

"We have examined a version of the familiar H-O-S analysis, with two countries, two commodities and two factors; we have made all the normal assumptions except that, instead of a common zero rate of profit, we have assumed a common positive rate of profit. Since the existence of a positive profit rate does not affect the properties of the familiar relationship between commodity-prices and factor-prices it does not affect the factor-price-equalisation and Stolper-Samuelson theorems. In general, however, nothing can be said a priori about the relationship between factor-prices and the factor-intensity of production methods, when the profit rate is positive, and it follows that nothing can be said a priori about the shape of the relative supply curve. This does not prevent the H-O-S theorem about the pattern of trade from holding in its 'quantity' form, but does make the theorem invalid in its 'price' form, does mean that trade need not 'harm' a country's scarce factor, and does mean that uniqueness of international equilibrium is to be regarded as a special case when the common rate of profit is positive." - Steedman and Metcalfe (1977)

The demonstration in Steedman and Metcalfe (1977) draws on an earlier analysis of a closed economy, Metcalfe and Steedman (1972). Here M. and S. present a reswitching example with two homogeneous unproduced inputs, labor and land. They find, at a certain given positive rate of profit, that the technique of production that minimizes cost at the higher ratio of the rent to wage will be more land-intensive. I think of this example as analogous to one of capital-reversing. It too is destructive of supply and demand explanations of prices.

I don't recall if they say so explicitly, but this article certainly gives the impression that this counter-intuitive result - at least to those who believe in the out-dated neoclassical theory of value and distribution - is due to the presence of reswitching. If I recall correctly, this result was later shown to be compatible with the absence of reswitching. I believe Steedman selected the article first demonstrating this compatibility for republication in Steedman (1989).

If I ever get around to discussing recent empirical results on the labor theory of value, I will point to some criticisms of Steedman.

Update: Radek reminds me that Montet (1979) demonstrated that the results in Metcalfe and Steedman (1972) and in Steedman and Metcalfe (1977) are compatible with the absence of reswitching.

References

• Metcalfe, J. S. and I. Steedman (1972). "Reswitching and Primary Input Use", Economic Journal (Reprinted in Fundamental Issues in Trade Theory (edited by I. Steedman), Macmillan, 1979).
• Steedman, I. and J. S. Metcalfe (1977). "Reswitching, Primary Inputs and the Heckscher-Ohlin-Samuelson Theory of Trade", Journal of International Economics (Reprinted in Fundamental Issues in Trade Theory (edited by I. Steedman), Macmillan, 1979).
• Metcalfe, J. S. and I. Steedman (1974). "A Note on the Gain From Trade", Economic Record (Reprinted in Fundamental Issues in Trade Theory (edited by I. Steedman), Macmillan, 1979).
• Montet, C. (1979). "Reswitching and Primary Input Use: A Comment", Economic Journal, V. 89, N. 355 (Sep.): 642-647.
• Steedman, I. (editor, 1989). Sraffian Economics (2 volumes), Edward Elgar.

Capitalism Seen As Unfree In Its Infancy

A charactistic transaction under capitalism is the selling of labor power for money wages. How was this transaction perceived in capitalism's early days? Consider:

"[the commonwealth] consisteth only of freemen... Day labourers ... have no voice nor authority in our commonwealth, and no account is made of them but only to be ruled ... [those who] be hired for wages ... be called servants." -- Thomas Smith (1565)

"If the common people have no more freedom in England but only to live among their elder brothers and work for them for hire, what freedom have they in England more than we have in Turkey or France? ... The poor that have no land are left still in the straits of beggary, and they are shut out of all livelihood but what they shall pick out of sore bondage, by working for others as masters over them." -- G. Winstanley (1649)

"Rather than go with cap in hand and bended knee to gentlemen and farmers, begging and entreating to work with them for 8d. or 10d. a day, which doth give them an occasion to tyrannize over poor people (which are their fellow-creatures), if poor man would not go in such a slavish posture..." -- R. Coster (1649)

"[The relations of employer and wage labourer] approach much nearer to that of a planter and slave in our American colonies than might be expected in such a country as England." -- Josiah Tucker (1757)

"...the ingenuity and dexterity of [England's] working artists and manufacturers, which have heretofore given credit and reputation to British wares in general [whose skill was] owing to that freedom and liberty they enjoy to divert themselves in their own way... Were they obliged to toil the year round, the whole six days in the week, in a repetition of the same work, might it not blunt their ingenuity and render them stupid instead of alert and dexterous?" -- M. Postlethwayt (1774)

All quotes are secondhand from:

• Christopher Hill (1967). "Pottage for Freeborn Englishmen: Attitudes to Wage Labour in the Sixteenth and Seventeenth Centuries," Socialism, Capitalism, & Economic Growth: Essays Presented to Maurice Dobb, Cambridge University Press.

Unregulated International Trade Unjustified By Comparative Advantage (TOC)

• Part 1
• Part 2
• Part 3
• Part 4
• Part 5