One Technique Replacing Another: An Example

Figure 1: The Wage Frontier at a Four-Technique Patterns

1.0 Introduction

This post presents another numerical example of one technique replacing another, along the wage frontier, with a perturbation of a model parameter.

In a previous post, I identified three sequences of patterns of switch points in which the wage curves for one technique replaces the wage curve of another. In one of these sequences, a three-technique pattern removes the middle technique from three techniques with wage curves on the wage frontier. A further perturbation of the model parameter of concern results in another three technique pattern, in which the wage curve for a new technique appears in the middle of the wage frontier. In a limiting case of this sequence of patterns, the distance in the parameter space between the two three-technique patterns reduces to zero. A four-technique pattern results.

The parameter that is increased, in this case, is not a coefficient of production. Rather, I consider a model in which barriers to entry, or some such idiosyncratic property of investment in specific industries, results in maintaining specified ratios of the rates of profits among industries. One of these ratios is the parameter that is varied in the numerical example. I have applied my pattern analysis in a limited way to such a model before. By the way, although others have recently analyzed such a model, I find that Ian Steedman outlines this model in his 1977 book, Marx after Sraffa.

This example is more complicated than previous examples of four-technique patterns. At the switch point in which the wage curves for four techniques intersect, processes in two industries are both changed. This is a fluke case - a pattern of co-dimension two, in my terminology. But, in the example, the process in a third industry does not vary with the cost-minimizing techniques around the switch point. The example also illustrates variation in the sequence of switch points, at another region in the wage frontier, with the perturbation of a model parameter. I am not totally happy with this example. The wage curves are often curved more sharply than is seen in real-world data. If I am going to look at a three-commodity example, I would like to find one where at least two wage curves intersect three times for positive, feasible rates of profits.

When I applied the terminology of co-dimension to patterns, I expected that it would be difficult to find, through numerical experimentation, examples of patterns of higher co-dimension. I expected I would have to consciously try to create them, as I did for this example of a global pattern. I argued at one point that patterns of co-dimension one are important for seeing how the sequence of switch points along the wage frontier can change with technical progress or changes in the strength of barriers to entry and so on. I am now leaning towards thinking this argument applies to at least some patterns of higher co-dimension.

Anyways, this example illustrates complications that can arise in price theory that I do not think have been previously noted.

2.0 Technology

The technology in this example is almost the same as in one of my previous examples. I modified one labor coefficient. The economy produces a single consumption good, called corn. Corn is also a capital good, that is, a produced commodity used in the production of other commodities. In fact, iron, steel, and corn are capital goods in this example. So three industries exist. One produces iron, another produces steel, and the last produces corn. Two processes exist in each industry for producing the output of that industry. Each process exhibits Constant Returns to Scale (CRS) and is characterized by coefficients of production. Coefficients of production (Table 1) specify the physical quantities of inputs required to produce a unit output in the specified industry. All processes require a year to complete, and the inputs of iron, steel, and corn are all consumed over the year in providing their services so as to yield output at the end of the year.

Table 1: The Technology

Input	Iron Industry		Steel Industry		Corn Industry
	a	b	c	d	e	f
Labor	1/3	1/10	5/2	7/20	1	3/2
Iron	1/6	2/5	1/200	1/100	1	0
Steel	1/200	1/400	1/4	3/10	0	1/4
Corn	1/300	1/300	1/300	0	0	0

A technique consists of a process in each industry. Table 2 specifies the eight techniques that can be formed from the processes specified by the technology. If you work through this example, you will find that to produce a net output of one bushel corn, inputs of iron, steel, and corn all need to be produced to reproduce the capital goods used up in producing that bushel.

Table 2: Techniques

Technique	Processes
Alpha	a, c, e
Beta	a, c, f
Gamma	a, d, e
Delta	a, d, f
Epsilon	b, c, e
Zeta	b, c, f
Eta	b, d, e
Theta	b, d, f

Each technique is represented by coefficients of production. For the Alpha technique, let a_{0, α} be a three-element row vector representing the labor coefficients, and let A_α be the 3 x 3 Leontief matrix for this technique. The first element of a_{0, α}, (1/3) person-years per ton, represents the labor input needed to produce a ton of iron. The first column of A_α represents the inputs of iron, steel, and corn needed to produce a ton of iron. A parallel notation is used for the other seven techniques.

3.0 The Price System

Prices of production are defined to be constant spot prices that allow the smooth reproduction of the economy. Suppose Alpha is the cost-minimizing technique. Let p be the three-element row matrix designating the prices of iron, steel, and corn. I make the assumption that markets are such that the rate of profits in the iron, steel, and corn industries are (r s₁), (r s₂), and (r s₃), respectively. Suppose S is a diagonal matrix with the obvious elements along the diagonal, and I designates the identity matrix. Then prices of production satisfy the following system of equations:

p_α A_α (I + r S) + w_α a_{0, α} = p_α

I choose a bushel of corn to be the numeraire. If e₃ is the last column of the identity matrix, the following equation specifies the numeraire:

p_α e₃ = 1

As is not surprising, the above system of equations has one degree of freedom. One can solve for the wage, w_α(r), as a function of the scale factor for the rate of profits, r. The is a downward-sloping curve that intercepts both the axis for the wage and the scale factor at positive values. A similar function can be derived the other techniques, and they can be graphed in the same diagram.

4.0 The Choice of Technique

Figure 2 graphs the wage curves for all eight techniques, given specific values for the mark-ups, s_i, i = 1, 2, and 3. The outer envelope, called the wage frontier, represents the cost-minimizing technique for any given wage or scale factor for the rate of profits. (Although it is difficult to see in the graph, the Theta technique is cost-minimizing for a continuum of the wage between two switch points.) Notice that only two wage curves intersect at each switch point on the frontier. The techniques that are cost-minimizing at each switch point differ in only one process. This is a non-fluke example, for these markups. For what it is worth, the switch point between the Delta and Gamma techniques exhibits capital-reversing.

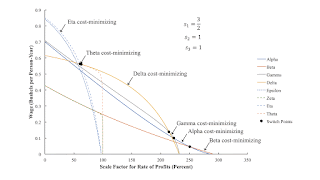
Figure 2: The Wage Frontier Before a Four-Technique Pattern

Table 3 shows the sequence of techniques that are cost-minimizing, along the wage frontier, at selected values of the markup for the iron industry. Figure 1, at the top of the post, illustrates the middle row. Presumably, two three-technique patterns have removed the Alpha and Gamma techniques from the frontier, for high values of the scale factor for the rate of profits. For the purposes of this post, I am not interested in those patterns. My point is focused on the switch point between the Eta and the Delta technique. Looking above at Table 2, one can see that, for these techniques, both processes in both the iron and corn industries are part of cost-minimizing techniques at the switch point. It follows that the Gamma and Theta techniques are cost-minimizing at this switch point, even though they do not appear on the wage frontier elsewhere. This is a fluke.

Table 3: Cost-Minimizing Techniques

s1	s2	s3	Techniques
3/2	1	1	Eta, Theta, Delta, Gamma, Alpha, Beta
2.665	1	1	Eta, Delta, Beta
4	1	1	Eta, Gamma, Delta, Beta

Finally, Figure 3 shows the wage frontier at the last level of the markup in the iron industry that I want to consider. The sequence of cost-minimizing techniques of Eta, Theta, and Delta, for relatively low scale factors for the rate of profits, has been replaced by the sequence of Eta, Gamma, and Delta. This example shows one sequence for how the wage frontier can be varied by lasting changes in a markup in one industry.

Figure 3: The Wage Frontier After a Four-Technique Pattern

5.0 Conclusion

Simple numerical examples are often presented in textbooks, such as Kurz and Salvadori's Theory of Production. They are often meant to illustrate phenomena that can appear in a more complicated example of a model. This post is an illustration of a fairly complicated example, where parts, in some sense, resemble simpler examples.

One Technique Replacing Another

Figure 1: One Way One Technique Can Replace Another

The wage-rate of profits frontier (or wage frontier) is calculated with prices of production, given the techniques of production, available in the economy, for producing a given output. Suppose at one point in time, the techniques that lie along the wage frontier consist of the Alpha, Beta, and Gamma techniques, in order of an increasing rate of profits. As time passes, technical innovation alters coefficients of production, including for techniques that were not on the wage frontier at the initial point in time. Suppose at a later point in time, the techniques along the wage frontier now consist of the Alpha, Delta, and Gamma techniques. How did this replacement of the Beta technique by the Delta technique occur? What happened in the intervening time interval?

The pattern analysis I have been developing suggests answers to these questions. A pattern is a qualitative characterization of a part of the wage frontier associated with a change of switch points. And the patterns I have identified suggest three possibilities for the postulated change in techniques.

Figure 1, above, illustrates the first possibility. These illustrations are only schematic; the illustrated curves need not be straight lines. In the first pattern, two three-technique patterns succeed one another in time. A three-technique pattern arises when a switch point on the frontier is an intersection of the wage curves for three techniques. For the temporally first three-technique pattern, a switch point is replaced by two switch points, with a new technique being cost-minimizing for rates of profits between the two switch points. Four techniques, instead of three techniques, now lie on the wage frontier. For the later three-technique pattern, two switch points are replaced by one switch point. The middle technique at the original point in time is no longer cost-minimizing, for any rate of profits. The postulated initial sequence of techniques occurs before the first pattern, and the final sequence occurs after the second pattern.

A second possibility is that a reswitching pattern is followed by two three-technique patterns. (The shape of the curves are definitely off in Figure 2.) For the reswitching pattern, a new switch point occurs at which the wage curves for two techniques are tangent. For some time afterwards, this possibility is a case of reswitching. The two three-technique patterns remove the wage curve for the originally middle technique from the wage frontier. Once again, the postulated observations for the first and last point in time are consistent with this story.

Figure 2: A Second Way One Technique Can Replace Another

A third possibility (Figure 3) also involves a sequence of two three-technique patterns. In this case, the temporally first three-technique pattern removes the wage-curve for the middle technique from the wage frontier. The wage frontier now has a succession of two cost-minimizing techniques along it. The second three-technique pattern puts a new technique in the middle of the wage frontier.

Figure 3: A Third Way One Technique Can Replace Another

Two other stories can arise out of symmetries of, at least, the first and second possibility. And one might complicate the story by superimposing wage curves for other techniques somewhere in this story. In my exploration of numerical examples, I have usually found the switch points in reswitching examples disappearing with patterns over the axis for the rate of profits and the wage axis. That is not the case here.

I think that wage curves can be calculated from Leontief matrices, as derived from the National Income and Product Accounts (NIPA). Zonghie Han & Bertram Schefold and Stefano Zambelli have calculated wage frontiers from empirical data. But I think confirming these stories of technical change fit data is a challenge for those who know more about empirical research following on from Leontief's work. I suspect one would have to look at stylized facts, in some sense. I think I have been developing a perspective on technical innovation that would be worth exploring for empirical applications, even if I am not the one to do this.

Marx Versus Classical Economics

Marx can be read as both a continuation and a critique of classical economics. A not-too-radical reading might emphasize his claim to find distinctions in economic theory glossed over by classical economists such as Adam Smith and David Ricardo. According to Marx, classical economists (as opposed to vulgar economists such as Frédéric Bastiat, Jean-Baptiste Say, and and Nassau William Senior) penetrated beneath surface phenomena to reveal the anatomy of capitalism. A more radical reading questions the soundness of the classical theory, while historicizing its emergence as a necessary illusion. The spokesmen for the emerging and progressive capitalist class sought for a theory justifying their opposition to aristocrats and the ancien régime. And classical economics was that theory.

This post presents three distinctions offered in the first, less radical reading. Marx had great respect for classical economists. I do not think he was always fair to them, insofar as he accused them of error by reading muddle into them for not seeing his new ideas. In this post, I do not document this charge by citing specific passages in, for example, Theories of Surplus Value. So more work would need to be done to extend this from a mere blog post. (This 8 January 1868 letter from Marx to Friedrich Engels is apposite here.) I also put aside the transformation problem here.

First distinction: between labor and labor power. Marx distinguishes between the capability of a member of the proletariat to work under the direction or control of a capitalist and the work done under that direction. The former is a commodity, labor power. The latter is the use value of that commodity, that is, labor. Both Marx and Ricardo treated labor power, like all commodities, as representing a certain quantity of embodied labor, namely, the labor value of the commodities necessarily consumed by the laborers, taking as given certain conventions about the hours and severity of work, the standard of living of the workers, the size of their families, which members were expected to work, and so on.

Without this distinction, Ricardo writes about such nonsense as the labor value of labor. (I need a direct quote here.) Marx argues that Ricardo is also unable to explain why capitalists are able to regularly generate profits. I suppose one could expand on this to analyze some of the evident difficulties in understanding Ricardo.

Second distinction: Between surplus value and profits, rent, and interest. Surplus value, for Marx, is the value added by labor not paid out in wages. It is an abstraction, akin to (some of) Ricardo's profits before his chapter on rent. Marx focuses on surplus value in the first volume of Capital. Surplus value is manifested at a more concrete level in the form of profits, rent, and interest on financial instruments. Would Ricardo's work be better if he had a separate label for surplus value?

Third distinction: Between prices of production and labor values. William Petty, Adam Smith, and David Ricardo all have a theoretical conception of market prices and natural prices. Natural prices are centers of gravity, in some sense, around which market prices fluctuate. Marx offered a trichotomy of market prices, prices of production, and labor values. The price of production, sometimes called the cost price, is Marx's equivalent for Smith and Ricardo's natural value. Marx can criticize passages in the classical economists for confusing prices of production and labor values. (A further confusion is that between the labor commanded by and the labor embodied in a commodity.)

I conclude with noting some complications not to be found in the above schematic divisions. In speaking of the labor value of labor power, I am implicitly assuming that all wages are consumed, and that wages are paid in commodities. But some workers, especially those deemed skilled, are able to save, even over and above what they need for a conventional retirement. And wages are paid in money, with the general level of prices of wage goods only determined after a bargain with workers has been struck.

In talking about surplus value, I have ignored the possibility of profits on alienation. This case has to be considered in a complete taxonomy of capital. Traders and speculators look for the possibility of bargains, of buying low and selling high. Both classical economists and Marx were aware of this possibility.

In speaking of labor values and prices of production, I seem to be assuming that all firms in an industry use the same processes and have the same costs. But Marx looks at variations in such processes. (I am never sure whether the processes that Sraffa takes as given should be the best practice or an average process. Perhaps, which is correct might vary among industries.) Finally, one might add a fourth distinction in Marx's theory of absolute rent, which is not to be found in the classical economists.

Another Way Reswitching Can Appear

Figure 1: Wage Curves for a Reswitching Example

1.0 Introduction

This post illustrates another fluke case. In this example economy, two techniques exist for producing a net output of corn. The wage curves for the two techniques have two switch points. One switch point is on the wage axis, corresponding to a rate of profits of zero. The other is on the axis for the rate of profits, corresponding to a wage of zero.

This example is a fluke in two ways. In the jargon I have been inventing, it is simultaneously a pattern across the wage axis and a pattern over the axis for the rate of profits. It differs from this previous example in that the switch points in both patterns arise for the same pair of techniques. In my jargon, it is a global pattern.

I created this example by simplifying and perturbing this one.

2.0 The Model

As usual, managers of firms know of a number of production processes (Table 1). A single commodity - a ton iron, a ton steel, or a bushel corn in the example - is the output of each process. Each process lasts a year and exhibits constant returns to scale. Inputs are defined in physical units, as indicated in the column for the iron-producing process. All inputs are used up in production; there is no fixed capital or joint production.

Table 1: The Technology for a Three-Industry Model

Input	Iron Industry	Steel Industry	Corn Industry
			Alpha	Beta
Labor	1/3 Person-Yr.	1/2	0.061628	0.420472
Iron	1/6 Ton	1/200	1	0
Steel	1/200 Ton	1/4	0	0.070079
Corn	1/300 Bushel	1/300	0	0

Two techniques are available. The Alpha technique consists of the iron-producing process, the steel-producing process, and the corn-producing process labeled Alpha. The Beta technique consists of same iron-producing and steel-producing processes, with the corn-producing process replaced by the one labeled Beta.

The choice of technique in a capitalist economy is assumed here to be based on cost-minimization for prices of production. Prices of production, for each technique, are characterized by a system of three equations in which the same rate of profits is earned in all three industries, for the processes comprising the technique. I assume that labor is advanced, and wages are paid out of the surplus. And I take a bushel corn as the numeraire.

Under these assumptions, one can draw the wage curve for each technique, as in Figure 1. The outer frontier of the wage curves illustrates the cost-minimizing technique. In the example, the Beta technique is cost-minimizing whatever the distribution of income. It is not uniquely cost-minimizing, however, for the switch points. In the two cases of a zero rate of profits and a wage of zero, any linear combination of the two techniques is cost-minimizing.

3.0 Conclusion

Suppose the coefficients of production for the corn-producing process in the Alpha technique were slightly higher. Then no switch points would exist, and the Beta technique would be uniquely cost-minimizing, whatever the distribution of income between wages and profits. The coefficients in the example illustrate a boundary case, just as technical progress creates a situation where prices of production arise for a case of reswitching. If technical progress were to decrease the coefficients of production for the Alpha process, the switch points would be closer together and further from the axes. It might be that what I am now calling a reswitching pattern might never occur. Some other processes for producing iron or steel might supplant the ones in the example, like in this previous example.

Books That Seem Interesting

I am thinking of maybe buying one of these:

• Roger E. Backhouse (2017). Founder of Modern Economics: Paul A. Samuelson: Volume 1: Becoming Samuelson, 1915-1948
• Robert Leonard (2012). Von Neumann, Morgenstern and the Creation of Game Theory: From Chess to Social Science, 1900-1960
• Philip Mirowski and Edward Nik-Khan (2017). The Knowledge We Have Lost in Information: The History of Information in Modern Economics
• Angela Penrose (2017). No Ordinary Woman: The Life of Edith Penrose
• Yanis Varoufakis (2017). Adults in the Room: My Battle with the European and American Deep Establishment. Update: Josh Mason has a review

I already have many books on which I am behind, for instance, Anwar Shaikh's Capitalism. I suspect the Penrose biography will strike me like Adelman's biography. I've read some of the economics the subject produced, but did not know about the Nazi-fighting.