Foreign Trade And Non-Uniform Rates Of Profits

This post raises a question. Supposedly, the classical concept of prices of production with non-uniform rates of profits can be recast as a theory of foreign trade. I do not see how wages can properly be treated in such recasting.

D'Agata (2018) and Zambelli (2018) are two recent papers that argue prices of production can be formulated with non-uniform rates of profits. They argue that this introduces a certain indeterminateness into prices, as in some of my examples of foreign trade. Both D'Agata and Zambelli cite Adam Smith and David Ricardo to justify their models as of classical inspiration. If somebody is to draw on this research for a theory of foreign trade, I hope they cite this passage from Adam Smith:

… every individual … endeavors as much as he can both to employ his capital in the support of domestic industry, and so to direct that its produce may be of the greatest value; every individual necessarily labours to render the of the society as great as he can. He generally, indeed, intends to promote the public interest, nor knows how much he is promoting it. By preferring the support of domestic to that of foreign industry, he only intends his own security; and by directing that industry in such a manner as its produce may be of the greatest value, he intends only his own gain, and he is in this, as in so many other cases, led by an invisible hand to promote an end which was no part of his intention.

I suspect many propertarians are not aware that Smith was arguing that a lack of foreign direct investment is desirable, that enough barriers exist against entrepreneurs investing in other countries that no need exist for certain protectionist laws to be passed by government.

D'Agata models non-uniform rates of profits as arising due to both "objective and idiosyncratic factors affecting producers' investment decisions". Objective factors are modeled by different groups of producers having access to different techniques of production for producing the same commodities. For example, firms in England and Portugal might have access to different techniques for producing corn and wine, as in Ricardo's Principles. I guess countries having different endowments of land and labor, thereby limiting the scale at which some processes can be operated, is also an objective factor important to the theory of foreign trade.

Idiosyncratic factors are formalized by different producers having different valuation functions, where a valuation function is a continuous, strictly increasing function of the rate of profits obtained in a given industry. In terms of the theory of foreign trade, one might model entrepreneurs in England all having identical valuation functions, while entrepreneurs in Portugal have another valuation function, common among the Portuguese. Each valuation function might be assumed not to vary among industries. For example, English entrepreneurs value the rate of profits made in making corn the same as the rate of profits made in making wine.

From these considerations, one can obtain a theory of foreign trade in which:

• Countries differ among themselves in the technology or endowments they have access to.
• In a full employment position with balanced trade, countries specialize in the production of different commodities.
• In such an equilibrium position, the rate of profits varies among countries.

(I do not claim such a theory is complete, since it does not consider Keynesian effective demand, paths with unbalanced trade, fluctuations in exchange rates, and so on.)

When I have tried to develop such a theory of foreign trade, I have created examples in which the wage also varies across countries. This is easy to justify based on an assumption of a lack of a free movement of people across national borders. But how is this idea formalized in D'Agata's approach?

References

• Antonio D'Agata, 2018. Freeing long-period prices from the uniform profit rate hypothesis: A general model of long-period positions. Metroeconomica 69: 847-861.
• Stefano Zambelli, 2018. Production of commodities by means of commodities and uniform rates of profits. Metroeconomica 69: 791-819.

Variation Of Gains From Trade With International Prices

Figure 1: Intercepts of Production Possibilities Frontiers for England

1.0 Introduction

In this example, gains and losses from trade vary with international prices. Given rates of profits are compatible with an interval of relative international prices for linen and corn, when trade exists only in consumer goods. I explore whether, when trade exists in capital and consumer goods, more than one pattern of specialization among countries is possible, depending on relative international prices. I am beginning to think that specialization, in this model, in corn and linen is infeasible, except in knife-edge cases.

The theory of comparative advantage provides no valid justification for the abolition or the lowering of tariffs. Unregulated international trade is not about efficient use of an international allocation of resources. Many existing textbooks, including Krugman and Obstfeld's, should be ripped up, and the authors should start again.

2.0 Technology, Endowments, And The Rate Of Profits

I assume each of two countries (Tables 1 and 2) have a fixed-coefficients technology for producing three commodities. The technology varies between countries, although it has the same structure in both. Steel is the only capital good. Each commodity can be produced, in a year, from inputs of labor and steel. A coefficient of production shows the quantity of an input needed per unit output. For example, in England, one person-year and 1/30 tons of steel must be purchased per square meter of produced linen. Steel is totally used up in production, and constant returns to scale obtains.

Table 1: Coefficients of Production in England

Inputs	Industry
	Steel	Corn	Linen
Labor	a0, 1(E) = 1	a0, 2(E) = 8	a0, 3(E) = 12
Steel	a1, 1(E) = 1/5	a1, 2(E) = 1	a1, 3(E) = 1

Table 2: Coefficients of Production in Portugal

Inputs	Industry
	Steel	Corn	Linen
Labor	a0, 1(P) = 6/5	a0, 2(P) = 12	a0, 3(P) = 20
Steel	a1, 1(P) = 1/4	a1, 2(P) = 2	a1, 3(P) = 3/2

I take endowments of labor as given, as in the Ricardian model of foreign trade. Let England and Portugal both have available a labor force consisting of one person-year. So Production Possibilities Frontiers (PPFs) are found per person-year. By assumption, workers neither immigrate nor emigrate. In this model, full employment is assumed.

I also take the rate of profits as given, at 100 per cent in England and at 20 percent in Portugal. I assume that financial capital cannot flow between countries. So the rate of profits need not be the same across countries.

3.0 Summary

I apply my usual analysis to determine patterns of specialization, given technology, endowments, and rates of profits in each country. When foreign trade is possible in corn and linen, but not steel, the domestic price of steel and the wage in each country must be such that the going rate of profit is earned in producing steel. Likewise, firms in, say, England make neither extra profits nor incur extra costs in producing the consumer good in which England specializes. The firms would incur extra costs if they were to produce the other consumer good. The same principles extend to the case in which foreign trade is possible in all produced commodities.

In this analysis, which is an example of a small country model, prices for goods bought or sold in foreign trade are taken as given by firms in all countries. I find prices and specializations which are consistent with the given parameters. One can draw Production Possibility Frontiers (PPFs) for each country, given prices in foreign markets and specializations. A PPF shows possible baskets of consumer goods when labor is fully employed. In this model, each PPF is a decreasing function in the first sector of the two-dimensional space formed by quantities of corn and linen. Such a PPF is fully specified by the intercepts. The intercept with the corn axis is maximum amount of corn that can be consumer, per employed worker, given that no linen is consumed. Similarly, the intercept with the linen axis is the maximum amount of linen that can be consumed. Figure 1, above, and Figure 2, show the intercepts for the PPFs for England and Portugal, respectively.

Figure 2: Intercepts of PPFs for Portugal

In the example:

• When foreign markets exist only for corn and linen:
• England specializes in the production of linen (and steel), while Portugal specializes in corn (and steel).
• England suffers a loss from trade, except when the international relative price of linen is at its highest feasible level.
• Portugal obtains a gain from trade.
• England’s loss and Portugal’s gain is smaller for larger relative prices of linen on international markets.
• When foreign markets exist for steel, corn, and linen:
• For a relatively small ratio of the international price of linen to the international price of corn, England specializes in corn and linen, and Portugal specializes in steel.
• In this range, prices compatible with England specializing in linen and Portugal specializing in steel and corn provide England with extra profits in producing corn.
• This case is infeasible. England only obtains steel by trading corn for it. England is unwilling to trade linen for steel, and Portugal is unable to acquire linen by selling steel.
• For a relatively large ratio of the international price of linen to the international price of corn, England specializes in linen, and Portugal specializes in steel and corn.
• In this range, prices compatible with England specializing in corn and linen and Portugal specializing in steel provide Portugal with extra profits in producing corn.
• England obtains a gain from trade, as compared to when foreign trade is only possible in consumer goods
• For a low price of linen in this range and a consumer basket heavily weighted to corn, England suffers a loss from trade, as compared to autarky.
• Otherwise, England obtains a gain from trade, as compared to autarky.
• Portugal’s PPF is identical to what it would be if foreign trade were possible only in consumer goods.
• Accordingly, Portugal obtains a gain from trade, as compared to autarky.

Gain or Loss from Trade with Multiple Equilibria

Figure 1: Production Possibility Frontiers

1.0 Introduction

Suppose foreign trade is possible in consumption goods, but not in capital goods. In this example, whether or not England achieves gains from trade depends on relative international prices. If foreign trade were possible in both consumption and capital goods, both England and Portugal would obtain gains from trade. The numeric example in this post is a modification of one in a previous post.

As I understand it, most students of economics are taught this numeric example cannot exist. And it raises questions on, for example, tariffs and the distribution of income that you will be hard-pressed to find discussed.

2.0 Technology, Endowments, And The Rate Of Profits

I assume each of two countries (Tables 1 and 2) have a fixed-coefficients technology for producing three commodities. The technology varies between countries, although it has the same structure in both. Steel is the only capital good. Each commodity can be produced, in a year, from inputs of labor and steel. A coefficient of production shows the quantity of an input needed per unit output. For example, in England, one person-year and 1/30 tons of steel must be purchased per square meter of produced linen. Steel is totally used up in production, and constant returns to scale obtains.

Table 1: Coefficients of Production in England

Inputs	Industry
	Steel	Corn	Linen
Labor	a0, 1(E) = 2	a0, 2(E) = 3	a0, 3(E) = 1
Steel	a1, 1(E) = 1/20	a1, 2(E) = 1	a1, 3(E) = 1/30

Table 2: Coefficients of Production in Portugal

Inputs	Industry
	Steel	Corn	Linen
Labor	a0, 1(P) = 2	a0, 2(P) = 7	a0, 3(P) = 2
Steel	a1, 1(P) = 1/40	a1, 2(P) = 1	a1, 3(P) = 1/100

I take endowments of labor as given, as in the Ricardian model of foreign trade. Let England and Portugal both have available a labor force consisting of one person-year. So Production Possibilities Frontiers (PPFs) are found per person-year. By assumption, workers neither immigrate nor emigrate. In this model, full employment is assumed.

I also take the rate of profits as given, at 25 per cent, in both countries. I originally intended to assume that financial capital cannot flow between countries. So the rate of profits need not be the same across countries.

3.0 One of Two Equilibria

One can analyze each country under autarky, that is, under the assumption that foreign trade is not possible. One can find, given the rate of profits in each country, relative prices of corn and linen in each country. Suppose foreign trade is possible in corn and linen, but not in steel. And suppose the ratio of the international price of linen to the international price of corn is between the corresponding ratio of autarkic prices in England and Portugal. (I have chosen the rates of profits so this ratio is lower in England than in Portugal under autarky.) Then the English specialize in producing linen, and the Portuguese specialize in producing corn. I consider international prices at the two extreme ends of this range. This section presents the first extreme.

3.1 Trade in Corn and Linen

Table 3 present prices and costs when trade is only possible in corn and linen. I follow the notation in a previous post. The rows show the international price of corn, the international price of linen, wages in each country, the domestic price of steel, the cost of producing corn, and the cost of producing linen. If anybody wants to work it out, wages and the price of steel are such that the given rate of profits is made in producing steel in each country.

Table 3: Trade in Consumer Goods

Variable	England	Portugal
P2	$15 per Bushel
P3	$49/17 per Sq. Meter
w(n)	$45/17 Person-Yr.	$155/99 per Person-Yr.
p1(n)	$96/17 per Ton	$320/99 per Ton
p1(n)a1,2(n)(1 + r(n)) + a0, 2(n) w(n)	$15 per Bushel	$15 per Bushel
p1(n)a1,3(n)(1 + r(n)) + a0, 3(n) w(n)	$49/17 per Sq. Meter	$314/99 per Sq. Meter

Firms in a country will only produce a commodity if its cost of production does not exceed its price. With the prices in the above table, the English are willing to produce both corn and linen, while the Portuguese produce only corn. I want to ignore that the English might want to produce corn. If the price of linen on international markets was just an infinitesimal higher, the English would not be willing to produce corn.

The upper half of the figure at the top of this post illustrates this case. When, at these prices, England specializes in linen, they obtain a loss from trade. Portugal obtains gains from trade throughout.

3.2 Trade in Steel, Corn, and Linen

I now consider this case with foreign trade in steel also. Table 4 shows prices and costs. The first row is for the price of steel on international markets. I also introduce a row for the cost of producing steel. With the same logic as above, I ignore that England can produce steel, as well as corn and linen, with these prices. I take the international prices of corn and linen as unchanged from the previous subsection.

Table 4: Trade in Capital and Consumer Goods

Variable	England	Portugal
P1	$96/17 per Bushel
P2	$15 per Bushel
P3	$49/17 per Sq. Meter
w(n)	$45/17 per Person-Yr.	$93/34 per Person-Yr.
P1 a1,1(n)(1 + r(n)) + a0, 1(n) w(n)	$96/17 per Ton	$96/17 per Ton
P1a1,2(n)(1 + r(n)) + a0, 2(n) w(n)	$15 per Bushel	$891/34 per Bushel
P1a1,3(n)(1 + r(n)) + a0, 3(n) w(n)	$49/17 per Sq. Meter	$471/85 per Sq. Meter

In this case, both England and Portugal gain from trade. England specializes in corn and linen, and Portugal specializes in steel. The possible consumption baskets for both England and Portugal, under trade in all commodities, is also shown in the upper half of the figure at the top of this page. Even if you click through, it is hard to see that the maximum amount of linen that can be consumed in England is strictly greater than autarky in this case. Samuelson calls the additional gains from trade obtained through foreign trade in capital goods as the "Sraffian bonus". I have previously shown that the Sraffian bonus can be negative.

4.0 A Second Equilibrium

Now suppose the international price of linen is at the opposite extreme, with the same specializations. Again, this is the endpoint of what should be an open interval.

4.1 Trade in Corn and Linen

Table 5 shows prices and costs when foreign trade is possible only in consumer goods. English firms make the going rate of profits in producing steel and linen, but would incur extra costs if they produced corn domestically. Portuguese firms make the going rate of profits in producing any of steel, corn, and linen. But I treat them here as specializing in producing corn for foreign trade and obtaining linen only through foreign trade.

Table 5: Trade in Consumer Goods

Variable	England	Portugal
P2	$15 per Bushel
P3	$314/99 per Sq. Meter
w(n)	$4710/1617 Person-Yr.	$155/99 per Person-Yr.
p1(n)	$10048/1617 per Ton	$320/99 per Ton
p1(n)a1,2(n)(1 + r(n)) + a0, 2(n) w(n)	$26690/1617 per Bushel	$15 per Bushel
p1(n)a1,3(n)(1 + r(n)) + a0, 3(n) w(n)	$314/99 per Sq. Meter	$314/99 per Sq. Meter

The bottom half of the figure above shows Production Possibility Frontiers for this case. Both England and Portugal obtain gains from trade. (The PPF for England, under trade in consumption goods, is not easy to visually distinguish from the PPF under autarky.) A given technology and given rates of profits is compatible with a country both obtaining gains and suffering losses from foreign trade in consumption goods, depending on international prices.

4.2 Trade in Steel, Corn, and Linen

International prices of corn and linen are the same in Table 6 below and Table 5 above. Table 6 is drawn up for the possibility of foreign trade in steel, corn, and linen. England specializes in corn and linen, and Portugal specializes in steel. As seen in the bottom half of the figure at the top of this post, both England and Portugal have gains in trade, as compared to autarky and to foreign trade in consumer goods, when trade is possible in all produced commodities.

Table 6: Trade in Capital and Consumer Goods

Variable	England	Portugal
P1	$1448/297 per Bushel
P2	$15 per Bushel
P3	$314/99 per Sq. Meter
w(n)	$2645/891 per Person-Yr.	$5611/2376 per Person-Yr.
P1 a1,1(n)(1 + r(n)) + a0, 1(n) w(n)	$11123/1782 per Ton	$1448/297 per Ton
P1a1,2(n)(1 + r(n)) + a0, 2(n) w(n)	$15 per Bushel	$181/8 per Bushel
P1a1,3(n)(1 + r(n)) + a0, 3(n) w(n)	$314/99 per Sq. Meter	$28417/5940 per Sq. Meter

5.0 Conclusion

In this example, only one process is known in each country for producing each commodity domestically. The possibility of foreign trade creates a choice of technique. I wonder if more processes existed for each country's technology, would the range of international prices for consumer goods consistent with certain national specializations be narrowed? Would the introduction of consumer demand in the model remove the indeterminism? I suppose, for exploring the last question, I should see what has been done with J. S. Mill's approach to analyzing foreign trade.

Elsewhere

• Matthew Klein writes, in Barron's, about "Tarrifs and the Minimum Wage Are More Alike Than You Think". I disagree with some of the stuff in the middle about efficiency and reject the dualistic notion that government intervention is a meaningful concept. But this article otherwise parallels some of my arguments here.
• Josh Mason has made available his piece in Jacobin about the state of economics after the global financial catastrophe.
• The Review of Political Economy has made available Pierangelo Garegnani's posthumous On the Labour Theory of Value in Marx and in the Marxist Tradition. I have yet to read Fabio Petri's introduction. Some points from Garegnani's article:
• Chapter 1 of volume 1 of Capital is not meant to be a proof of the Labor Theory of Value (LTV).
• The LTV fills an instrumental role in providing a calculation of the rate of profits prior to the system of prices of production.
• Much of volume 1 remains valid, even after correcting the mathematical theory. For a given technology, there is a trade-off between wages and the rate of profits. Capitalists try to increase relative and absolute surplus value.
• Marx's account of profits as the result of the exploitation of workers is descriptive, not a moral or ethical judgement.
• Rudolf Hilferding did not have the mathematical machinery (e.g., theorems on the principal Eigenvalue of a matrix) to counter Eugen Böhm von Bawerk's criticism of Marx. Consequently, his attempt is misdirected.

Gains And Losses From Foreign Trade: A Numeric Example

Figure 1: Production Possibility Frontiers

1.0 Introduction

This post presents a numeric example of foreign trade in a model of the production of commodities by means of commodities. This is a modification of the model here, which considers a flow-input, point output technology. As usual, I show neoclassical economics is mistaken. Frictions, increasing returns, information asymmetries, principal agent problems, and so on do not need to be introduced to explain why the outcomes of free markets are not always ideal. Even under ideal conditions, problems can arise.

2.0 Technology, Endowments, And The Rate Of Profits

I assume each of two countries (Tables 1 and 2) have a fixed-coefficients technology for producing three commodities. The technology varies between countries, although it has the same structure in both. Steel is the only capital good. Each commodity can be produced, in a year, from inputs of labor and steel. A coefficient of production shows the quantity of an input needed per unit output. For example, in England, one person-year and 1/30 tons of steel must be purchased per square meter of produced linen. Steel is totally used up in production, and constant returns to scale obtains.

Table 1: Coefficients of Production in England

Inputs	Industry
	Steel	Corn	Linen
Labor	a0, 1(E) = 2	a0, 2(E) = 3	a0, 3(E) = 1
Steel	a1, 1(E) = 1/20	a1, 2(E) = 1	a1, 3(E) = 1/30

Table 2: Coefficients of Production in Portugal

Inputs	Industry
	Steel	Corn	Linen
Labor	a0, 1(P) = 2	a0, 2(P) = 7	a0, 3(P) = 2
Steel	a1, 1(P) = 1/40	a1, 2(P) = 1	a1, 3(P) = 1/100

I take endowments of labor as given, as in the Ricardian model of foreign trade. Let England and Portugal both have available a labor force consisting of one person-year. So Production Possibilities Frontiers (PPFs) are found per person-year. By assumption, workers neither immigrate nor emigrate. In this model, full employment is assumed.

I also take the rate of profits as given, at 300 per cent, in both countries. I originally intended to assume that financial capital cannot flow between countries. So the rate of profits need not be the same across countries. (If you find the rate of profits unacceptably high, read "year" as "decade" throughout this post.)

3.0 Aspects of Autarky

Suppose all three commodities are each produced in each country. Foreign trade is not possible. The technology allows one to calculate the labor embodied in each commodity. For steel, the number of person-years embodied in each ton of steel is:

v₁(n) = a_{0, 1}(n)/(1 - a_{1, 1}(n))

The labor embodied in corn and linen is:

v_j(n) = a_{0, 1}(n) a_{1, j}(n)/(1 - a_{1, 1}(n)) + a_{0, j}(n), j = 2, 3.

Labor values are useful in drawing the PPF for each country, under autarky. Consumers in England can consume 1/v₂(E) bushels of corn per person-year of labor hired, if they consume no linen. Or they can consume 1/v₃(E) square meters per person-year, with no corn. Any linear combination of these two consumption baskets, with positive quantities of both corn and linen, can also be consumed.

Each PPF embodies a rate of transformation between corn and linen, in a comparison of stationary states. For example, in England 61 bushels of corn can be traded off, in some sense, for 291 square meters of line. England has a comparative advantage in linen, as compared to corn, at a rate of profits of zero.

v₃(E)/v₂(E) < v₃(P)/v₂(P)

Portugal has a comparative advantage in steel, as compared to both corn and linen, at a rate of profits of zero.

4.0 Trade in Corn and Linen

In this section, I assume that foreign trade is possible in the consumer commodities, corn and linen. But international markets do not exist in the capital good, steel. The introducition of the possibility of foreign trade creates a choice of technique.

In the small country model, firms take prices, including on international markets, as given. I introduce the following notation:

• P₂: The price of a bushel corn on international markets.
• P₃: The price of a square meter of linen on international markets.
• w(n), n = E, P: The wage.
• r(n), n = E, P: The rate of profits.
• p₁(n), n = E, P: The domestic price of steel.
• p₁(n)a_1,2(n)(1 + r(n)) + a_{0, 2}(n) w(n), n = E, P: The cost of producing a bushel corn domestically.
• p₁(n)a_1,3(n)(1 + r(n)) + a_{0, 3}(n) w(n), n = E, P: The cost of producing a square meter of linen domestically.

Table 3 shows the value of each of these variables. Firms will not produce commodities when their cost of producing it exceeds what it can be purchased for on international markets. Accordingly, England specializes in producing linen and the necessary steel at these prices. Portugal produces corn and linen. The domestic price of steel and wages are such that firms cannot make extra profits in steel, corn, or iron production.

Table 3: Trade in Consumer Goods

Variable	England	Portugal
P2	$6 per Bushel
P3	$2/3 per Sq. Meter
w(n)	$19/32 Person-Yr.	$117/286 per Person-Yr.
p1(n)	$35/64 per Ton	$69/88 per Ton
p1(n)a1,2(n)(1 + r(n)) + a0, 2(n) w(n)	$127/32 per Bushel	$6 per Bushel
p1(n)a1,3(n)(1 + r(n)) + a0, 3(n) w(n)	$2/3 per Sq. Meter	$1869/2200 per Sq. Meter

The ratio of the prices of linen and corn are a key variable here. Countries specialize in the consumer commodity in which relative international prices exceeds the domestic relative price, as calculated under autarky. Since the rate of profits is positive, relative domestic prices differ from the slope of the autarkic PPF. That is, the relative autarky price is what determines comparative advantage, in some sense. But the slope of the autarkic PPF is important in analyzing whether gains from trade are positive or negative.

The possibility of foreign trade in consumer goods has made consumers in England worse off, in a comparison of stationary states. The English PPF is rotated inwards, when firms specialize as induced by these prices. Consumers in Portugal, on the other hand, are better off. Their PPF is rotated outwards.

4.0 Trade in Steel, Corn, and Linen

I now assume trade is possible in all goods, including the capital good. Let P₁ be the price of steel on international markets. Cost of domestic production are modified in the obvious way in Table 4.

Table 4: Trade in Capital and Consumer Goods

Variable	England	Portugal
P1	$10/9 per Bushel
P2	$6 per Bushel
P3	$2/3 per Sq. Meter
w(n)	$14/27 Person-Yr.	$1/2 per Person-Yr.
P1 a1,1(n)(1 + r(n)) + a0, 1(n) w(n)	$34/27 per Ton	$10/9 per Ton
P1a1,2(n)(1 + r(n)) + a0, 2(n) w(n)	$6 per Bushel	$143/18 per Bushel
P1a1,3(n)(1 + r(n)) + a0, 3(n) w(n)	$2/3 per Sq. Meter	$47/45 per Sq. Meter

England specializes in the production of corn and linen, and Portugal specializes in the production of steel. Firms in England obtain the steel they need to continue production by trading corn and linen in foreign trade. Likewise, consumers in Portugal obtain corn and linen from firms selling the surplus steel product in foreign trade. No firm incurs extra costs or obtains extra profits in any process which they operate. And operated process would incur extra costs.

The opening up of foreign markets in steel has made England better off, both in comparison to autarky and in comparison with foreign trade only being possible in consumer goods. (Although it is difficult to see in Figure 1, the intercept of the PPF, for trade in all commodities, with the ordinate strictly exceeds the intercept for the other PPFs). The opening up of foreign trade in steel has made Portugal worse off, as compared to trade only in consumer goods. Whether the Portuguese are better off as compared to autarky is ambiguous. It depends on the consumption basket.

5.0 Conclusion

Why, oh why, do mainstream economists teach untruths about the theory of trade?

A Country Worse Off With Trade In Capital Goods

Figure 1: PPFs in Portugal

1.0 Introduction

This post continues these two posts. I change the model here to have wages advanced, not paid out of the surplus at the end of the year.

I here consider an example of a model of stationary states in which two countries can trade in produced commodities to be used for consumption. The countries face given prices on international markets for traded commodities. (They are small open economies, in the jargon.) I take the rate of profits as given in each country. They may differ, since I assume that finance capital cannot be traded internationally. I also assume labor is immobile between countries.

I contrast the model with and without foreign trade being possible in capital goods. Paul Samuelson calls the supposed gains from trade in capital goods the Sraffian bonus. This post demonstrates that the Sraffian bonus can be negative. The inhabitants of a country might be better off, in the sense that the total bundle of consumption goods is larger, if international markets do not exist in capital goods.

2.0 Parameter Values

I assign the numeric values in Table 1 to coefficients of production. For those who do not want to click, a unit of steel can be made in England from a direct and unassisted labor input of l_{2, C, E} person-years. A unit of corn can be made from one unit of steel and l_{1, C, E}. A unit of linen is made from l_{1, L, E} person-years of direct and unassisted labor.

Table 1: Technology for the Example

Parameter	England	Portugal
l1, C, n	3	7
l2, C, n	2	2
l1, L, n	1	2
Ln	1	1
rn	300%	400%

I take the endowments of labor - L_E and L_P person-years, respectively - as given. Production Possibility Frontiers (PPFs) are constructed per worker.

I also take rates of profits, r_E and r_P, as given. I do not strive for realism. But, if you are concerned by the sizes of the rates of profits, pretend that my "year" is actually a decade or so.

3.0 Stationary States with and without Trade in Capital Goods

I now consider what prices could be consistent with stationary states.

First, suppose foreign trade is not possible in capital goods. Only corn and linen can be traded on international markets. Suppose prices are as in Table 2. The cost of producing linen in England:

l_{1, L, E} w_E (1 + r_E) = 1 (1/6) (1 + 3) = 2/3

If firms in England manufacture linen for both domestic consumption and for foreign trade, they make the going rate of profits. The cost of producing corn in England is:

[l_{2, L, E} (1 + r_E) + l_{1, L, E}] w_E (1 + r_E) = [2 (4) + 3](1/6)(4) = 22/3

Firms in England will not want to produce corn. They would be undercut by foreign competition. You can do the analogous calculations for Portugal. Portuguese firms will produce corn and the needed steel to continue production. They will not produce linen. With these prices and this specialization, consumers in both countries can consume baskets of commodities containing both corn and linen. And firms will be minimizing costs.

Table 2: Example with Foreign Trade in Corn and Linen

Variable	England	Portugal
PC	6
PL	2/3
Cost of producing corn	22/3	6
Cost of producing linen	2/3	12/7
Specialization	Linen	Corn and Steel
wn	1/6	6/85

Suppose now that international markets exist in corn, linen, and steel. Table 3 shows prices for consideration in this case. One tabulates the cost of producing corn with the steel input evaluated at the international price. For example, the cost of producing corn in England is:

(P_S + l_{1, C, E} w_E) (1 + r_E) = [1 + 3 (1/6)](4) = 6

Going through these tabulations, one will find that the firms in England specialize in producing corn and linen. The cost of producing steel in England exceeds its price. Likewise, firms in Portugal specialize in producing steel. Cost-minimizing firms in Portugal are unwilling to produce either corn or linen.

Table 3: Example with Foreign Trade in Corn, Linen, and Steel

Variable	England	Portugal
PC	6
PL	2/3
PS	1
Cost of producing corn	6	17/2
Cost of producing linen	2/3	1
Cost of producing steel	4/3	1
Specialization	Corn and Linen	Steel
wn	1/6	1/10

Notice that the international prices of corn and linen are unchanged between Tables 2 and 3. Steady states are here shown as resulting in an increased wage in Portugal when foreign trade is possible in steel. But rates of profits and the wage in England are shown as constant.

3.0 Production Possibility Frontiers

What about physical quantities of commodities? I restrict myself to stationary states. Figure 2 shows PPFs in England. The PPF under autarky is constructed from technical data on coefficients of production and the endowment of labor in England. When only linen is produced in England, whether foreign trade is possible or not, the same amount of linen is produced as under autarky. Consequently, all three PPFs are shown as rotated around the same intercept in Figure 2.

Figure 2: PPFs in England

Consider England when foreign trade is only possible in corn and linen. Since England specializes in linen, the maximum amount of corn consumed by the English is (L_E/l_{1, L, E})(P_L/P_C). In this example, that quantity is less than L_E/(l_{1, C, E} + l_{2, C, E}), the maximum quantity of corn consumed in England without foreign trade.

When foreign trade is also possible in steel, the maximum quantity of corn manufactured in England is (L_E/l_{1, C, E}) units. But not all of this corn can be consumed. Steel must be purchased from Portugal to continue production on the same scale. That is, (L_E/l_{1, C, E})(P_C - P_S) numéraire units are available for consumption. So the maximum corn consumption in England is (L_E/l_{1, C, E})(P_C - P_S)/P_C units of corn. For England, the Sraffian bonus is positive. The possibility of foreign trade in steel has left the PPF for domestic consumption rotated outwards, even beyond the maximum consumption under autarky.

The situation in Portugal, as illustrated by Figure 1 at the top of this post, is quite different, however. Foreign trade in consumer, but not capital goods, results in a PPF rotated outwards from the autarkic PPF. This conforms to the nonsense long-suffering students in economics taught out of mainstream textbooks must endure. At the prices considered above, Portugal produces only steel when foreign trade is possible in all produced goods. The maximum amount of linen that can be consumed in Portugal is (L_P/l_{2, C, E})(P_S/P_L) units. Neither intercept with an axis for this PPF is equal to the corresponding intercept for autarky. Furthermore, the PPF with foreign trade in all goods is strictly inside the PPF with foreign trade only in consumer goods. The Sraffian bonus is negative. Suppose one compares the PPF with foreign trade in all goods to the autarkic PPF for Portugal. Whether or not there are gains from trade is ambiguous. It depends on the consumption basket.

4.0 Conclusion

So this post has extended long-ignored proofs that the theory of comparative advantage does not provide a valid a-priori argument for so-called free trade. Opening up markets in capital goods may not provide a country with more goods, setting aside problems of adjustment.

I know of some empirical work purporting to demonstrate gains from trade. I do not know of any that addresses the issues brought forth in this post.

References

• Paul A. Samuelson (2001). A Ricardo-Sraffa Paradigm Comparing Gains from Trade in Inputs and Finished Goods. Journal of Economic Literature 39, 4: 1204-1214.
• Ian Steedman (1980). Trade amongst Growing Economics. Cambridge University Press.

More On Foreign Trade In Consumer And Capital Goods

Figure 1: Rates Of Profits for Specialization in Consumer Goods

1.0 Introduction

This post is a continuation of this example. How a country specializes in foreign trade depends on distribution. And foreign trade can reduce the consumption basket to be divided among the inhabitants of a country, as compared with autarky.

2.0 Patterns of Specialization

Assume that the consumption basket in both countries contains both corn and linen. In a steady state, international prices and the distribution of income in both countries must be such that at least one country produces each one of the three commodities. Table 1 lists the six possible patterns of specialization in which each commodity is produced in exactly one country. If foreign trade is possible in consumer goods, but not in capital goods, steel must be produced in the same country in which corn is produced. Only cases 2 and 5 are possible. All six cases must be analyzed if foreign trade is possible in both consumer and capital goods.

Table 1: Patterns of Specialization

Case	England	Portugal
1	Corn	Linen, Steel
2	Linen	Corn, Steel
3	Steel	Corn, Linen
4	Linen, Steel	Corn
5	Corn, Steel	Linen
6	Corn, Linen	Steel

A pattern of specialization is compatible, given the technology, with certain rates of profits between the trading countries. Under the assumption that financial capital does not flow between countries, the rate of profits may vary between countries. Insofar as the determinants of distribution is unspecified, the model is open. A neoclassical closure would specify intertemporal utility-maximizing consumers in each country

Disequilibrium transitions paths are also not considered here. Firms could find their expectations, with which they have produced or bought capital goods, disappointed. Presumably along such paths, trade might be unbalanced, and exchange rates could vary. Keynesian considerations of effective demand come into play. The elasticities of the demands for imports and exports might be of some importance, as reflected in the Marshall-Lerner conditions. The convergence of such transition paths to steady states does not seem assured.

3.0 Trade in Consumer Goods

Consider the model under the assumption that international markets do not exist for steel. Suppose England specializes in the production of linen, and Portugal specializes in the production of corn, as in case 2. Then the international prices of linen and corn must be related:

l_{1, L, E}/(v_{C, E} + l_{2, C, E} r_E) < P_L/P_C

P_L/P_C < l_{1, L, P}/(v_{C, P} + l_{2, C, P} r_P)

Hence:

l_{1, L, E}/(v_{C, E} + l_{2, C, E} r_E) < l_{1, L, P}/(v_{C, P} + l_{2, C, P} r_P)

Or:

r_P < (l_{1, L, P} l_{2, C, E} r_E + l_{1, L, P} v_{C, E} - l_{1, L, E} v_{C, P})/(l_{1, L, E} l_{2, C, P})

A specific region in the space for the national rates of profits corresponds to each pattern of specialization. Figure 1, above, shows these two regions, as divided by the upward-sloping line. The figure is drawn under the assumption that England has a comparative advantage in producing linen.

4.0 Production Possibility Frontiers (PPFs)

A production possibility frontier (PPF) shows the upper limits on how much linen or corn can be consumed in a given country in a stationary state. Let Y_{C, n} represent bushels corn consumed, and let Y_{L, n} be the square-yards of linen consumed, where n = E or P for England or Portugal. Let L_E and L_P be the endowments of labor in England and Portugal, respectively.

I want to consider three PPFs. Here is the PPF for autarky, when a country does not have the possibility to engage in foreign trade:

l_{1, L, n} Y_{L, n} + v_{C, n} Y_{C, n} = L_n

The PPF for a country specializing in the production of corn is:

v_{C, n} (P_L/P_C)Y_{L, n} + v_{C, n} Y_{C, n} = L_n

The PPF for a country specializing in the production of linen is:

l_{1, L, n} Y_{L, n} + l_{1, L, n} (P_C/P_L) Y_{C, n} = L_n

Figure 2 graphs these PPFs. The possibility of foreign trade rotates the autarkic PPF, with the pivot on an axis, depending on which product the country specializes in. I have drawn the PPFs such that when the country specializes in the production of linen, it is worse off as a whole. If any corn is consumed at all, foreign trade results in a smaller commodity basket than under autarky.

Figure 2: Production Possibility Frontiers for One Country

4.1 Comparison of PPFs for Autarky and Specialization in Corn

For a country specializing in corn, the ratio of the international price of linen to the international price of corn is bounded above:

P_L/P_C < l_{1, L, n}/(v_{C, n} + l_{2, C, n} r_n)

For a non-negative rate of profits, the right-hand side cannot exceed l_{1, L, n}/v_{C, n}. Hence:

P_L/P_C < l_{1, L, n}/v_{C, n}

Or:

(L_n/l_{1, L, n}) < (L_n/v_{C, n})(P_C/P_L)

The left-hand side is the maximum consumption of linen for this country under autarky. The right-hand side is the corresponding maximum consumption when the country specializes in producing corn. Thus, in this simple model, specialization in corn when no foreign markets in steel exist, unambiguously rotates the PPF outwards. In a comparison of stationary states, foreign trade gives the country specializing in producing corn a greater consumption basket to distribute among its inhabitants.

4.2 Comparison of PPFs for Autarky and Specialization in Linen

On the other hand, specialization in linen could make a country worse off. For the PPF to be rotated inward, one must have:

(L_n/l_{1, L, n})(P_L/P_C) < (L_n/v_{C, n})

Or:

P_L/P_C < l_{1, L, n}/v_{C, n}

So a country experiences a loss from trade when it specializes in linen and the following condition holds:

l_{1, L, n}/(v_{C, n} + l_{2, C, n} r_n) < P_L/P_C < l_{1, L, n}/v_{C, n}

Notice a loss from trade is not possible when the rate of profits is zero.

Suppose rates of profits and prices are such that England specializes in the production of linen. Prices can be such that England can gain from trade if and only if:

l_{1, L, E}/v_{C, E} < l_{1, L, P}/(v_{C, P} + l_{2, C, P} r_P)

Or:

r_P < (l_{1, L, P} v_{C, E} - l_{1, L, E} v_{C, P})/(l_{1, L, E} l_{2, C, P})

The right-hand side can be positive if and only if England has a comparative advantage in producing linen when rates of profits are zero in both countries.

5.0 Conclusion

So in this simple model, when international markets exist in consumer goods, but not in capital goods:

• Which country specializes in producing corn and which in producing linen depends on domestic rates of profits.
• Only one pattern of specialization for a given pair of rates of profits is possible.
• For each pattern of specialization, a pair of rates of profits exists for that specialization.
• If a country specializes in producing corn, its PPF is rotated outwards.
• If a country specializes in producing linen, its PPF may be rotated outwards, but only if:
• The country has a (technologically-defined) comparative advantage in producing linen.
• The relative price of linen on international markets is high enough.
• The PPF may be rotated inwards when a country specializes in producing linen; the terms of trade matter.

I am finding it non-obvious how to complete this analysis when steel can be traded in foreign markets. Also, I should create numerical examples just to confirm my results.

Foreign Trade In Capital And Consumer Goods

Figure 1: Specialization In A Single Country

1.0 Introduction

This post considers how the firms in a small open economy will specialize, given prices on international markets and the domestic rate of profits. The example would only be interesting as part of a larger argument, which I have not yet worked out.

2.0 Technology

Consider a small, open economy which has a flow-input, point-output technology for producing two consumption goods, corn and linen. Corn is manufactured from inputs of direct labor and steel. Steel and linen are each manufactured from inputs of direct, unassisted labor. Table 1 shows an input-output table for the technology. The technology is thus specified by three coefficients of production, (l_{1, C, n}, l_{2, C, n}, and l_{1, L, n}).

Table 1: Example Technology

Input	Industry
	Steel	Corn	Linen
Labor	l2, C, n Person-Yrs	l1, C, n Person-Yrs	l1, L, n Person-Yrs
Steel	0	1 Ton	0
Linen	0	0	0
Corn	0	0	0
Output	1 Ton	1 Bushel	1 Square-Yd

Comparative advantage when the rates of profits is zero in each country is determined by relative ratios of labor embodied in each commodity. The labor value of steel is:

v_{S, n} = l_{2, C, n}

The labor value of corn is the sum of the labor embodied in steel used in producing corn and the direct labor used in producing corn:

v_{C, n} = l_{1, C, n} + l_{2, C, n}

The labor value of linen is:

v_{L, n} = l_{1, L, n}

For a technology in which dated labor inputs extend for a larger number of time periods, finding labor values can require the calculation of sums with a greater number of terms.

3.0 Autarky

In this section, I assume foreign trade is not possible for the country being analyzed.

Let p_{C, n}, p_{L, n}, and p_{S, n} be the domestic prices of corn, linen, and steel when no foreign trade is possible. Let w_n be the wage paid for a person-year of labor, and let r_n be the rate of profits. Assume labor is advanced and wages are paid out of the surplus at the end of the year.

Under these assumptions, prices, with labor-commanded as the numeraire, are:

p_{S, n}/w_n = l_{2, C, n} = v_{S, n}

p_{C, n}/w_n = v_{C, n} + l_{2, C, n} r_n

p_{L, n}/w_n = l_{1, L, n} = v_{L, n}

4.0 Trade in Consumer Goods

Now suppose foreign trade is possible in consumer goods, but not in capital goods. In terms of the example, the firm can trade in corn and linen, but not in steel. Let P_C and P_L be international prices of corn and linen, respectively.

Two patterns of complete specialization are possible. Suppose the firms in the country want to produce linen (and the required steel), but not corn. Linen is sold on international markets, and corn is purchased. For firms to be unwilling to produce corn, the cost of producing a unit of corn, at the going rate of profits, must exceed the given international price:

[l_{2, C, n}( 1 + r_n) + l_{1, C, n}] w_n > P_C

In a steady state, the cost of producing linen must be equal to its price:

l_{1, L, n} w_n = P_L

Solving for the wage and substituting, one obtains the following inequality.

P_L/P_C > l_{1, L, n}/(v_{C, n} + l_{2, C, n} r_n)

Or:

P_L/P_C > p_{L, n}/p_{C, n}

For domestic firms to want to specialize in producing corn, the above inequality is reversed. In words, the country specializes in producing those goods whose international prices exceed autarkic prices.

5.0 Trade in Capital and Consumer Goods

In this section, I assume that the country can trade steel on international markets, as well as corn and linen.

Suppose the country specializes in producing linen. The following inequalities and equalities must be satisfied in a steady state:

l_{2, C, n} w_n > P_S

P_S ( 1 + r_n) + l_{1, C, n} w_n > P_C

l_{1, L, n} w_n = P_L

Following my usual practice of solving for wages and substituting, I obtain two inequalities:

P_L > (l_{1, L, n}/l_{2, C, n}) P_S

P_L > (l_{1, L, n}/l_{1, C, n})[P_C - P_S ( 1 + r_n)]

When the country specializes in corn, the system of inequalities and equalities is modified in a way that I hope is obvious. As above, two conditions characterize prices on international markets. The same is true for when the country specializes in the production of steel. For the country to specialize in linen, it is necessary but not sufficient that the country would have specialized in linen in trade in steel were impossible. This is not so for specialization in corn. For some combinations of international prices, the country will specialize in corn even when the country would not have so specialized when trade in capital goods was not possible. Likewise, a set of prices exists in which the country specializes in steel when the country would have specialized in corn without the possibility of trade in steel.

6.0 Conclusion

Figure 1, at the head of this post summarizes the analysis. The upward-sloping line extending from the origin divides regions of specialization under the assumption that foreign markets exist for consumer goods, but not for capital goods. When the international prices of corn and linen are in the region above this line, the country specializes in producing linen. When they are in the region below this line, the country specializes in producing corn.

With the possibility of international trade in steel, additional regions appear. If prices of linen and corn are low enough, for a given price of steel, they fall in the rectangle at the lower left in the figure. The country specializes in steel. All of each year's output of steel is sold in foreign trade, and linen and corn are bought with the revenues thereby obtained. A wedge appears in the upper right. If prices are in this region, the country does not specialize in producing linen. It becomes more cost-effective to produce corn, with inputs of steel purchased on international markets.

On the Gain and Loss from Trade

I have written up my recent explorations in the theory of international trade.

Abstract: This article considers a model of international trade in which the number of produced commodities does not exceed the number of countries engaged in trade. Technology is modeled such that each commodity can be produced in each country from a finite series of dated labor inputs. The existence of a positive rate of profits may lead a country to specialize differently than how it would with a zero rate of profits. Trade may leave consumers in a country worse off, as compared with autarky, when the rate of profits is positive. The existence of more than two countries provides a possibility that the Production Possibilities Frontier (PPF) with trade is neither unambiguously above or below the PPF under autarky. This article re-iterates, in a setting with more than two produced commodities and more than two countries, demonstrations that the argument for free trade is logically invalid, given positive rates of profits.

Class Struggle And Specialization In International Trade

This post continues a previous numeric example. The firms in each of three countries are assumed to know a technology for producing corn, wine, and linen. The technology is such that each commodity can be produced in each country. The technology varies among countries.

Each of these small open economies can specialize and obtain non-produced commodities through foreign trade. I confine myself to patterns of specialization in which:

• Each country produces exactly one commodity domestically.
• Each commodity is produced in one country.

Six patterns of specializations meet these criteria. Table 1 lists the commodity produced in each country for each pattern of specialization.

Table 1: Patterns of Specialization

	England	Portugal	Germany
I	Corn	Wine	Linen
II	Corn	Linen	Wine
III	Wine	Corn	Linen
IV	Wine	Linen	Corn
V	Linen	Corn	Wine
V	Linen	Wine	Corn

I have found out that, in my example, each specialization is consistent with a long period position. I take the international price of corn as numeraire. That is, p₁ = 1. Table 2 lists the prices of the other commodities, p₂ and p₃, that are traded domestically. It also lists rates of profits, r₁, r₂, and r₃, in each country. This data is sufficient to calculate the wage in each country. The wage is such that supernormal profits are not earned in the commodity produced domestically, but the cost (including profits) does not exceed revenues for produced commodities. With these wages, the costs of producing a commodity in which a country does not specialize will exceed the price. It is cheaper in each country to acquire such commodities on international markets.

Table 2: International Prices and Rates of Profits

	Price of Wine	Price of Linen	Rate of Profits
			England	Portugal	Germany
I	3/4	2/3	0%	0%	0%
II	0.83	0.7	50%	0%	20%
III	0.883	3/4	20%	60%	0%
IV	1.06	1.3	60%	50%	90%
V	1.1	5/4	40%	150%	70%
VI	4/5	0.754	0%	20%	20%

The prices shown in Table 2 are not unique. For the given set of rates of profits, international prices must fall within a certain range to obtain a long period position consistent with the pattern of specialization. And rates of profits may vary in certain ranges too. I have not figured out a good way of visualizing how the spaces of prices and rates of profits is divided up by the patterns of specialization. Maybe a region for a given pattern of specialization if, contrary to this example, restitching was possible under autarky.

The numeric example illustrates that:

• The pattern of specialization in foreign trade can be driven by technology and the distribution of income.
• Only some distributions are compatible with all countries being able to specialize in a consistent way.
• The results of such specialization may not provide a country with overall gains from trade, nevermind individual groups defined by the functional distribution of income.

I have assumed constant returns to scale, but which commodity a country specializes in producing may be of importance because of considerations of learning-by-doing. Technological progress may be easier to obtain in some commodities (e.g., manufactured industrial products) than others (e.g., products of agriculture). I suspect these observations generalize to a more comprehensive Neo-Ricardian theory of trade, such as that of Yoshinori Shiozawa.

These theoretical observations, I guess, are enough to blow up much mainstream teaching on trade. I might have even made some progress on the work of Mainwaring, Metcalfe, and Steedman. Nevertheless, this model puts much aside. I am thinking of, especially, Keynesian issues of exports, imports, and effective demand; foreign exchange rates and monetary policy; and international finance.

The Gain And Loss From Trade: More On A Numeric Example

Figure 1: The Production Possibility Frontier, With And Without Trade, In "Germany"

1.0 Introduction

I continue to blunder around in parameter space in exploring my numeric example in the previous post. In this post, I continue to adopt the same assumptions for a model of three countries engaged in international trade with three produced commodities. In particular, workers are assumed to be unable to immigrate, capitalists only invest in their own country, and produced means of production are not traded. Thus, wage rates and rates of profits may vary among countries, with no tendency to change or approach equality.

2.0 Outline of the Model

For this intellectual exercise, I make the same assumptions about technology, available in each country, but differing among them. Corn, wine, and linen can each be produced from a dated series of labor inputs. Under the restrictive assumptions illustrated by the numeric example, one can rank commodities by how labor-intensive they are. Corn is most labor-intensive, and linen is least. Wine is of an intermediate labor-intensive. The endowment of labor is also taken as given.

The rate of profits is taken as given in each country. One then wants to find a set of international prices for corn, wine, and linen such that a pattern of specialization can arise for the given data. Under a model of small, open economies, the firms in each country take prices as given. In such specialization, each country will specialize in producing at least one commodity, and each commodity will be produced in one or another country. The wage in each country will be such that no pure economic profits (also known as supernormal profits) will be earned in the production of any commodities. And costs, including charges for the prevailing rate of profits, will exceed the price of all commodities that firms in each country are unwilling to produce.

3.0 Countries Specializing in Producing One Commodity

Table 1 exhibits a set of prices, for the given rates of profits, that meets these conditions. Each country specializes in the production of one commodity. England produces linen, Portugal produces corn, and Germany produces wine. The wages in each country are as shown.

Table 1: Prices with Trade

Commodity	England	Portugal	Germany
Corn	p1 = 3240/11
Wine	p2 = 324
Linen	p3 = 4050/11
Rate of Profits	r1 = 2/5	r2 = 3/2	r3 = 7/10
Wage	w1 = 4050/1199	w2 = 162/121	w3 = 1

For this particular set of prices, each country specializes differently than they would if the rates of profits were zero in each country. And they specialize differently than they would at the prices and positive rates of profits in my previous exploration of this example.

4.0 Production Possibility Frontiers (PPFs)

In the textbook theory of comparative advantage, an unambiguous gain from trade is shown by comparing the Production Possibilities Frontier (PPF) with trade and under autarky. The claim is that the with-trade PPF is moved outward from what it would be under autarky. If the consumption basket contains any commodities that must be bought on international markets, the with-trade equilibrium is supposedly unambiguously better for the country. No commodity must be consumed in a smaller amount than under autarky, and some commodities can be produced in larger quantities. Some may be hurt by trade, perhaps because they receive profits from industries whose domestic production has been replaced by imports. But they could be compensated out of the increased consumption basket, while still leaving everybody else better off in the country under consideration.

To check the textbook argument, one would look at the PPFs in each of England, Portugal, and Germany. And the textbook story is validated for England in this numeric example, with these prices and pattern of specialization. The PPF for England is rotated outwards, as compared with autarky. They coincide at the intersection with the linen axis. For every other consumption basket with non-negative quantities, the English with-trade PPF lies outside the autarkic PPF. England gains from trade.

The with-trade and autarkic PPFs for Portugal (Figure 2) replicate my previous finding that specialization can result in a loss from trade. The argument from comparative advantage is logically invalid, given positive rates of profits among countries engaged in international trade. The with-trade PPF in Portugal is rotated inwards. Portugal is unambiguously worse off with trade.

Figure 2: The Production Possibility Frontier, With And Without Trade, In "Portugal"

The story from Germany illustrates a possibility that cannot arise in the two-country, two-commodity model. The with-trade PPF (Figure 1) is neither rotated outwards nor inwards, as compared with the autarkic PPF. Along one dimension (linen), the with-trade PPF lies outside the autarkic PPF. Along another dimension (corn), it lies inside the autarkic PPF. Whether Germany is worse or better off with-trade depends on the composition of the commodity basket.

5.0 Remarks on Krugman and Obstfeld

I am unsure what I think of Krugman and Obstfeld, so far. Chapter 2 presents the argument from comparative advantage. They hammer home that, in the Ricardian model, countries are better off with-trade, no question about it. In this chapter, inputs consist only of labor, and no profits are earned. I do not know that they are clear that labor inputs are only direct. (In my example, I have labor inputs distributed over time, thereby providing a role for a rate of profits.)

In Chapter 3, they have manufacturing goods produced from labor and capital, as specified by a production function. I am not sure they ever take the marginal product of capital. They show output as a function of labor, with a diminishing marginal product. Although they do have some remarks on the supply of labor, they seem to be considering a medium term model where manufacturing output is produced with given technical conditions and a given set of production facilities. The point is to show that trade has impacts on the distribution of income in a country and can hurt some, if they are not compensated out of the supposed gains.

Chapter 4 sets out the Heckscher-Ohlin-Samuelson model in the two-factor, two-country, two-commodity case. The factors are labeled labor and land. This is as far as I've gotten in my reading.

One reading of the above is that Krugman and Obstfeld are carefully working around the Cambridge Capital Controversy. I do not know that they entirely succeed in Chapter 3. Their chapters have points, and I, of course, question their Chapter 2 claim that the gains of trade are unambiguously positive. Presumably, they would point to later chapters that put forth qualifications about imperfect competition and increasing returns to scale - a textbook presentation of the work that won Krugman a Nobel prize. Or they might point to a need in pedagogy to drum home simple points. Furthermore, their textbook, they could argues, teaches what (mainstream) economists have settled on as a consensus of what international economics is.

But what happens when the consensus has been shown to be simply wrong almost half a century ago? I know I have previously thought Krugman's offhand remarks on his blog about the CCC did not seem particularly informed. Has he ever referenced, say, Ian Steedman, in his academic work?

References

• Paul R. Krugman and Maurice Obstfeld (2003). International Economics: Theory and Policy, sixth edition.

The Loss From Trade: A Numeric Example With Three Countries And Three Produced Commodities

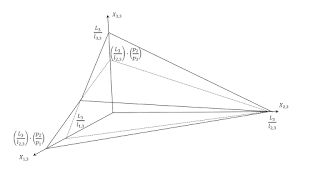
Figure 1: The Production Possibility Frontier, With And Without Trade, In "Germany"

1.0 Introduction

This post presents a numeric example of a Ricardian model of small, open economies engaged in trade. Each of three countries specializes in producing one of three commodities. Technology is modeled following an Austrian approach. Each commodity can be produced in each country from inputs of labor and "capital". Endowments of labor are taken as given parameters. It makes no sense to take the endowment of capital as a given parameter.

The with-trade Production Possibilities Frontier (PPF) can be compared to the autarkic PPF in each of the three countries. And it is unambiguously rotated inwards in one country for the set of international prices and rates of profits I consider. One cannot correctly conclude, in the traditional textbook approach, that free trade makes the inhabitants of a country better off in the aggregate.

I have previously written up an analogous argument in the two-commodity, two-country case. I should have cited Steedman and Metcalfe (1973). If I had, I would have known that my originality was less than I suggested. Shiozawa argues convincingly that the sort of model illustrated in this post can only be offered as an intellectual exercise. A more empirically applicable model would have trade in intermediate products, and the number of traded commodities would exceed the number of countries. On the other hand, I do not know of any comparable write-up of an example with three or more commodities and countries, as here.

2.0 Assumptions

Consider a model of three countries - England, Portugal, and Germany - in which three commodities are potentially traded on international markets by each country.

• Each country can produce any of the three commodities.
• The managers of firms in each country know a given flow input-point output technology with the structure described in Section 3. The technology differs among countries.
• Each country has a given endowment of labor, the only non-produced factor of production in each country. The endowment of labor may vary between countries.
• Only commodities produced for consumption can be traded internationally. Workers can neither immigrate nor emigrate. Intermediate goods, also known as capital goods, cannot be traded internationally.
• Financial capital is only invested domestically. Consequently, the rate of profits may vary across countries.
• Free competition obtains in all domestic markets; transport costs are negligible; and free trade exists in all commodities produced for consumption.

3.0 Technology

In each country, each commodity can be produced by a uniform application of labor for a specified number of years (Table 1). In each country, less total labor is required to produce a unit wine than is required to produce a unit of corn, with the labor uniformly distributed over a longer period of time in producing wine. Wine is a less labor-intensive and more capital-intensive commodity than corn, in some sense. In the same sense, linen is a less labor-intensive and more capital-intensive commodity, as compared with wine. England has an absolute advantage over Portugal, and Portugal has an absolute advantage over Germany, in producing each commodity. Nevertheless, a set of prices on international markets can exist, for corn, wine, and linen, such that firms in each country will want to specialize in producing a single commodity.

Table 1: Example Technology

Produced Commodity	Years of Labor	Labor Input per Year (Person-Yrs)
		England	Portugal	Germany
Corn	1	100	220	320
Wine	2	40	75	120
Linen	3	25	45	200/3 ≈ 66.6

The data on technology, along with the endowment of labor in each country, is enough to draw the Production Possibility Frontier (PPF) for each country in an autarky (without trade). Let X_{1, n}, X_{2, n}, and X_{3, n} be the quantity of corn, wine, and linen consumed in the nth country (n = 1, 2, 3). The plane outlined by the heavy lines in Figure 1, above, is the autarkic PPF for Germany. L₃ is the endowment of labor in Germany. l_{1, 3}, l_{2, 3}, and l_{3, 3} is the labor embodied in each commodity, when produced in Germany. These quantities are 320, 240, and 200 labor-years for this technology.

4.0 Prices and Specialization With Trade at a Rate of Profits of Zero

Next, consider an equilibrium with trade. Suppose the prices of a unit of corn, wine, and linen are as in Table 2. The question arises of whether there is a pattern of specialization among countries and a distribution of income in each country consistent with the given international prices. At this point, I take the rate of profits as zero. And I have calculated the wages shown for each country.

Table 2: Prices with Trade with Zero Rate of Profits

Commodity	England	Portugal	Germany
Corn	p1 = $300
Wine	p2 = $225
Linen	p3 = $200
Rate of Profits	r1 = 0	r2 = 0	r3 = 0
Wage	w1 = $3	w2 = $3/2	w3 = $1

Table 3 shows relative prices in each country, where the numeraire varies among countries. That is, a person-year of domestic labor is taken as the numeraire. (In Table 2, I have implicitly taken German labor - the lowest paid, as numeraire.) Notice that, in Table 3, the prices of corn in England, wine in Portugal, and linen in Germany are all equal to the labor values in the respective countries. And the prices of all other commodities falls below their labor values. Thus, since the rate of profits is zero, English firms will specialize in producing corn, Portuguese firms will produce only wine, and German firms will produce only linen. To obtain a domestic consumption basket, in any country, that contains all three commodities, each country must engage in international trade. It turns out that the PPF is unambiguously rotated outward for each country, for a pattern of specialization with a rate of profits of zero.

Table 3: Renormalized Prices with Zero Rate of Profits

Commodity	England	Portugal	Germany
Corn	p1/w1 = 100	p1/w2 = 200	p1/w3 = 300
Wine	p2/w1 = 75	p2/w2 = 150	p2/w3 = 225
Linen	p3/w1 = 200/3	p3/w2 = 400/3	p3/w3 = 200

5.0 Prices and Specialization With Trade at Positive Rates of Profits

It is well-known that, in general, prices deviate from labor values when the rate of profits is positive. Suppose the prices of corn, wine, and linen are as shown in Table 4. I also take the rates of profits as given in each country. These data yield the wages shown in the Table.

Table 4: Prices with Trade

Commodity	England	Portugal	Germany
Corn	p1 = 4275/26
Wine	p2 = 9063/52
Linen	p3 = 855/4
Rate of Profits	r1 = 3/5	r2 = 1/2	r3 = 9/10
Wage	w1 = 9063/5408	w2 = 1	w3 = 855/1664

I suppose the fractions are somewhat less awkward when normalized, as in Table 3. Unlike the case with a zero rate of profits, one should not compare these prices with labor values, in order to figure out the pattern of specialization. Rather, one should compare these prices with dated labor inputs costed up at the going rate of profits. For example, consider England. Since corn is produced with only one year of labor, its labor cost is still 100 person-years. (I am assuming wages are paid at the end of the year, not advanced.) Since p₁/w₁ is less than 100, England will import corn and not produce any. The cost of wine is 40(1 + 3/5) + 40 = 104. England will produce wine, and no super-normal profits are earned in its production. Linen is costed up as 25(1 + 3/5)² +25(1 + 3/5) + 25 = 129. p₃/w₁ is, approximately, 127.55. It is more costly to produce linen domestically, and, so, England will not do that. As a result of similar calculations, one can see that Portugal will specialize in producing linen and Germany in corn. The prices permit a consistent pattern of specialization, with all commodities being produced in some country and no firm earning more than the going rate of profits. And every country specializes in producing a different commodity shown above for the pattern with a zero rate of profits.

Table 3: Renormalized Prices

Commodity	England	Portugal	Germany
Corn	p1/w1 = 5200/53	p1/w2 = 4275/26	p1/w3 = 320
Wine	p2/w1 = 104	p2/w2 = 9063/52	p2/w3 = 1696/5
Linen	p3/w1 = 128440/1007	p3/w2 = 855/4	p3/w3 = 416

One can draw the PPFs, for each country, with this pattern of specialization and prices on international markets. The PPFs for England and Portugal are rotated out. For any consumption basket that contains some commodity not produced domestically, more is available to the country as a whole in England and Portugal. But the PPF is rotated inwards in Germany, as illustrated in Figure 1. The possibility of trade has diminished the commodities available for consumption in Germany.

6.0 Conclusion

I like that, in the above example, the pattern of specialization has each country producing a different commodity in the case with a positive rates of profits, as compared to the case with a rate of profits of zero. I'd like to convince myself that no other pattern of specialization is possible when the rate of profits is zero. I'd also like to find an example where the with-trade PPF is rotated outwards on one dimension and inwards on another. So whether every commodity in a nation's consumption basket is improved or decreased by trade would depend on its composition. I can show in the above model how a country's endowment of capital varies in value with the domestic rate of profits. And the model can be set out, in general, with any number of produced commodities and countries, with the number of commodities not exceeding the number of countries. In such a general setting, I think I will retain the severe restrictions of an Austrian model so as to exhibit that my point does not depend on, for example, capital-reversing.

It has been known for decades that the argument from comparative advantage is not a valid justification for a lack of tariffs (also known as free trade). Even setting aside such matters as, for example, increasing returns to scale or Keynesian failures of aggregate demand preventing a country from being on its PPF, the argument fails on its own terrain. This post is one more demonstration. Of course, this does not imply that any random, ill-natured, and ill-considered imposition of tariffs is likely to be a good idea in any specific case.

References

• Kurose, Kazuhiro and Naoki Yoshihara (2016). The Heckscher-Ohlin-Samuelson Model and the Cambridge Capital Controversies. Working paper.
• Metcalfe, J. S. and Ian Steedman. 1974. A Note on the Gain from Trade, Economic Record. Reprinted in Fundamental Issues in Trade Theory (Ed. by I. Steedman). Aldershot: Greg Revivals (1979, 1991).
• Shiozawa, Yoshinori. 2018. An Origin of the Neoclassical Revolution: Mill’s ‘Reversion’ and its Consequences.
• Steedman, Ian and J. S. Metcalfe. 1973. ’On Foreign Trade,’ Economia Internazionale. Reprinted in Fundamental Issues in Trade Theory (Ed. by I. Steedman). Aldershot: Greg Revivals (1979, 1991).
• Vienneau, Robert (2014). On the Loss from Trade