Bastard Keynesianism From Krugman

Consider this claim:

"Until John Maynard Keynes published The General Theory of Employment, Interest, and Money in 1936, economics - at least in the English-speaking world - was completely dominated by free-market orthodoxy. Heresies would occasionally pop up, but they were always suppressed. Classical economics, wrote Keynes in 1936, 'conquered England as completely as the Holy Inquisition conquered Spain.' And classical economics said that the answer to almost all problems was to let the forces of supply and demand do their job." -- Paul Krugman

A lot of historians of economics have been discussing this claim, under a thread titled "QUERY - All pre-1936 economists were laissez-faire advocates".

I want to consider why Krugman understates the impact of the General Theory, if you read this as a statement about policy. In Britain, some economists certainly opposed both the building of Keynesian institutions and fiscal countercyclical policy, as later promoted, for example, by Abba Lerner. As such opponents, I cite Hayek and Robbins at the London School of Economics and the "Treasury view". I also think that many economists were arguing for something like Keynesian policy.

But I think these "Keynesian" advocates were not basing themselves on a theory strongly integrated with the central neoclassical (Marshallian?) price theory. For example, American Institutionalists of the time could be accused of advocating "measurement without theory", as Koopmans later put it. And those, such as some Keynes' British colleagues, looking into business cycle theory or monetary theory could be accused of ad-hoc short term theory.

A Post Keynesian perspective is that Keynes was addressing this lack of theoretical support for pragmatic policy more than the lack of reasonable policy itself. He says so himself in the second sentence of the preface:

"But [this book's] main purpose is to deal with difficult questions of theory, and only in the second place with the applications of this theory to practice." - John Maynard Keynes, The General Theory of Employment, Interest, and Money, p. v

I find this perspective lacking in the HES discussion so far. (I do not want to argue, in this place, against any argument that, for example, (early) Joan Robinson is a source of what she later labeled "bastard Keynesianism.")

Mumpsimus

Apparently, Gary Becker and Richard Posner have an editorial in the 26 January 2007 issue of the Wall Street Journal. They oppose an increase in the minimum wage:

"An increase in the minimum wage raises the costs of fast foods and other goods produced with large inputs of unskilled labor. Producers adjust both by substituting capital inputs and/or high-skilled labor for minimum-wage workers and, because the substitutes are more costly (otherwise the substitutions would have been made already), by raising prices. " -- Gary Becker and Richard Posner

I know about this editorial from posts from Frederic Sautet and Don Boudreaux. Both Sautet and Boudreaux endorse Becker and Posner's "reasoning". When will economists accept arithmetic?

Welcome To The Party

Compare and contrast this:

"When Friedman was beginning his career as a public intellectual, the times were ripe for a counterreformation against Keynesianism and all that went with it. But what the world needs now, I'd argue, is a counter-counterreformation." - Paul Krugman (2007). Who Was Milton Friedman?, New York Review of Books, V. 54, N 2 (February 15)

And this:

"What professional economics now needs is a rebellion against supply and demand. We need a rebellion against the idea that people are actually paid in proportion to the value of what they produce. We need a rebellion against the metaphor of the labor market - an entity that no one has ever seen, where no one has ever been, an entity that lacks the mechanishms of price adjustment that would be required for the marginal productivity theory to work. Economics needs a rebellion that is almost less against the system under which we live, as against the sources of our complacency about that system. We need a rebellion, not so much as against existing market institutions, as against the analytical tyranny of the idea of the market, as it applies to pay.

[Footnote:] Such a rebellion almost got going in the 1960s, when a dispute known as the 'Cambridge controversies' challenged the concept of capital as a factor of production and hence the coherence of the notion of marginal productivity. But the marginal productivity theory of the labor market survived that challenge, and its success in so doing is the root of the difficulty today." - James K. Galbraith (1998). Created Unequal: The Crisis in American Pay, Free Press: 265-266

Steedman's Full Industry Equilibrium

Ian Steedman, over a couple of decades, has been considering a coherent comparative statics analysis of industries in equilibrium. He points out that all industries typically cannot be in equilibrium if just one input price, say, varies. More than one price must vary for the industries in the economy to remain in long-run equilibrium, that is, in what Steedman calls Full Industry Equilibrium (FIE). And he has produced many examples, often without reswitching or even capital-reversing, in which competitive firms facing Constant-Returns-to-Scale technology desire to employ more of an input per unit output when that input's price is higher.

Although he has occasionally taken excursions into consumer theory or the Heckscher-Ohlin-Samuelson (HOS) theory of international trade, Steedman's analysis is not of General Equilibrium. He does not consider utility maximization. Thus, he does not consider the supply of non-produced inputs or the demand for consumer goods. FIE does not imply that the economy as a whole is in equilibrium or that supply and demand match in every industry. It is an open partial analysis.

I read the earliest couple of these papers a while ago. (I reference them in my 2005 Manchester School paper.) But only in the last few years did I become aware that one of Steedman's research agendas is so focused.

• Opocher, Arrigo and Ian Steedman (2006). "Long-Run Rising Supply Price and the Numeraire", Discussion Papers in Economics, Manchester Metropolitan University, ISSN 1460-4906
• Opocher, Arrigo and Ian Steedman (2005). "The Industry Supply Curve: Two Different Traditions", Manchester Metropolitan University, ISSN 1460-4906
• Steedman, Ian (2006a). "Long Run Demand for Labour in the Consumer Good Industry", Metroeconomica, V. 57, N. 2: 158-164
• Steedman, Ian (2006b). "Differential Depreciation and the 2x2 Model of Distribution, Pricing and Production", Metroeconomica, V. 57, N. 1: 112-119
• Steedman, Ian (2005). "Long Run Input Use-Input Price Relations and the Cost Function Hessian" (working paper?)
• Steedman, Ian (2004). "Consumer Substitution Effects Under Full Industry Equilibrium", Metroeconomica, V. 55, N. 1: 41-48.
• Steedman, Ian (2003). "The Comparative Statics of Industry-Level Produced-Input-Use in HOS Trade Theory" (working paper?)
• Steedman, Ian (2002). "Process Recurrence and Input Use at the Industry Level: A Coherent Long-Period Analysis", Economic Issues, V. 17, P. 1 (March): 59-66
• Steedman, Ian (1998). "Produced Input Use Per Unit of Output", Economic Letters, V. 59: 195-199
• Steedman, Ian (1988). "Sraffian Interdependence and Partial Equilibrium Analysis", Cambridge Journal of Economics, V. 12: 85-95
• Steedman, Ian (1985). "On Input 'Demand Curves'", Cambridge Journal of Economics, V. 9, N. 2: 165-172

An Institutionalist Before Joan Robinson

"...An eminent professor of law once defined the legal mind in this way. If, he said, there are two things so closely related that one cannot be conceived except in terms of the other, but if you can think of one without thinking of the other, then you have a legal mind. In somewhat similar fashion it might be said that if two things are utterly and completely distinct, but if you nevertheless think of them as being identical, then you have an economic mind...

...This is the idea of capital. Unfortunately for all of us, it is quite false. As everybody knows, the progress of any society depends upon its ability to enlarge the productive apparatus of the community...But since money will buy anything in commercial society, those who control accumulations of money are in a position to buy and control the increasing productive apparatus that spells progress. Therefore, it seems that money is the instrument of progress...

...Some people call it nature, but others call it capital. Even in early modern times industry was growing fast. That growth was a function of the industrial equipment of the community, as anybody could see even in early times. To identify that function with the accumulation of money was to attribute the whole thing to the men who made money. This is what we accomplish by calling both things 'capital.' The argument runs as follows: Economic progress results from the growth of the material equipment of industry, that is to say, capital; capital, that is to say, money, is created by 'saving'; therefore economic progress is made possible by 'saving.' In this fashion the money power became functional.

...The double-talk of capital has become an ingrained habit. It runs through virtually every textbook. Textbook writers solemnly warn their students of confusion which lurk behind this word. Resolutely they insist that it must be used to refer to one thing or the other, and not both. With exemplary clarity they declare, for example, that they propose to use it to refer only to the physical equipment of industry: plant, machines, raw materials, and so forth. And in the very next paragraph we find them saying that capital is brought into existence by saving! But now, obviously, they are talking about money!

That is how it is done." -- C. E. Ayres, The Divine Right of Capital (1946)

Sicklied O'er With The Pale Cast Of Thought

"'In truth, however, value is here [in capital] the active factor in a process, in which, while constantly assuming the form in turn of money and commodities, it at the same time changes in magnitude, differentiates itself by throwing off surplus-vaule from itself; the original value, in other words, expands spontaneously. For the movement, in the course of which it adds surplus-value, is its own movement, its expansion, therefore, is automatic expansion. Because it is value, it has acquired the occult quality of being able to add value to itself. It brings forth living offspring, or, at the least, lays golden eggs...

In simple circulation, C-M-C, the value of commodities attained at the most a form independent of their use-values, i.e., the form of money; but the same value now in the circulation M-C-M, or the circulation of capital, suddenly presents itself as an independent substance, endowed with a motion of its own, in which money and commodities are mere forms which it assumes and casts off in turn. Nay, more: instead of simply representing the relations of commodities, it enters now, so to say, into private relations with itself. It differentiates itself as original value from itself as surplus value; as the father differentiates himself from himself qua the son, yet both are one and of one age: for only by the surplus-value of 10 pounds does the 100 pounds originally advanced become capital, and so on as this takes place, so soon as the son, and by the son, the father is begotton, so soon does their difference vanish, and they again become one, 110 pounds.' [Marx, Capital, V. 1, 171-173]

...Is capital, then, the true Subject/Substance? Yes and no: for Marx, this self-engendering circular movement is - to put it in Freudian terms - precisely the capitalist 'unconscious fantasy' which parasitizes upon the proletariat as the 'pure substanceless subjectivity'; for this reason, capital's speculative self-generating dance has a limit, and it brings about the conditions of its own collapse. This insight allows us to solve the key interpretative problem of the quote above: how are we to read its first three words, 'In truth, however'? First, of course, they imply that this truth has to be asserted against some false appearance or experience: the everyday experience that the ultimate goal of capital's circulation is still the satisfaction of human needs, that capital is just a means to bring this satisfaction about in a more efficient way. This 'truth', however, is not the reality of capitalism: in reality, capital does not engender itself, but exploits the worker's surplus-value. There is thus a necessary third level to be added to the simple opposition of subjective experience (of capital as a simple means of efficiently satisfying people's needs) and objective social reality (of exploitation): the 'objective deception', the disavowed 'unconscious' fantasy (of the mysterious self-generating circular movement of capital), which is the truth (although not the reality) of the capitalist process. Again - to quote Lacan - truth has the structure of a fiction: the only way to formulate the truth of capital is to present this fiction of its 'immaculate' self-generating movement. And this insight also enables us to locate the weakness of the 'deconstructionist' appropriation of Marx's analysis of capitalism: although it emphasizes the endless process of deferral which characterizes this movement, as well as its fundamental inconclusiveness, its self-blockade, the 'deconstructionist' retelling still describes the 'fantasy' of capital - it describes what individuals believe, although they don't know it." -- Slavoj Zizek (2006). The Parallax View, MIT Press: 59-60.

Reification and the Consciousness of the Proletariat

If you grow up in a capitalist society, like the United States, you will be inclined to all sorts of odd beliefs, about human nature, laws of economics, and earning one's pay, for example. These beliefs will condition how you feel about, for example, labor unions. Academic economics is an expression of this tendency. As such, the best it can be, without a lot of pushback from within and without, is confused. Since it is confused, one can find self-contradictions in its teachings, and one will find which theoretical trends are marginalized and which are valorized have little to do with the worth of their contents. (Note that one can argue about specific self-contradictions and the worth of specific trends independently of one's opinions about the above claims.)

I suggest that one can find some such claims in some of the texts of Karl Marx. And those specific texts are still worth exploring. I refer to, for example:

• The Poverty of Philosophy (I suppose specifically, Chapter II, The Metaphysics of Political Economy, is a more narrow reference)
• The distinction between "Classical political economy" and "Vulgar political economy" in the author's preface to the second edition of Capital
• Capital, Volume 1, Part 1, Chapter I, Section 4: The Fetishism of Commodities and the Secret Thereof
• Capital, Volume 3, Part Seven: The Revenues and Their Sources
• Theories of Surplus Value, Part III, Addenda: Revenue and Its Sources. Vulgar Political Economy

Nothing is New Under the Sun

A lot of neoclassical textbooks echo ideas developed by J. R. Hicks. I believe Shove's criticisms are still applicable to mainstream teaching.

"The central thesis is this: that if wage-rates generally are forced above 'the competitive level' (whatever exactly that may be), unemployment will be caused in two ways: (i) by the 'tendency for capital to shift from the less capitalistic to the more capitalistic trades' (and methods) ..., i.e. to 'those which use a relatively large proportion of capital to labour in making a unit of product' ..., from those which use a relatively small proportion; (ii) because 'the total supply of capital' will be diminished ..., since capital will be 'lost' ..., 'eaten into' ..., 'consumed' ..., 'destroyed' ..., 'cut into' ..., 'dissipated' ... or 'decumulated', and 'savings' therefore checked ... Unfortunately, 'capital' is not defined and we are not told how quantities of it (or indeed of labour) are to be measured, and similarly of 'saving'. Presumably, these are 'matters which properly belong to the theory of capital' ... But until they are cleared up it is impossible to follow Mr. Hicks's reasoning; and surely a theory of wages may not unreasonably be expected to include a precise and intelligible explanation of the processes through which wage-rates influence employment. For instance, it is not immediately apparent why employment should be diminished in the first of the two ways above distinguished...

...Again, Mr. Hicks excludes from consideration the monetary reactions of wage-policy. He recognises that 'the kind of processes we have been examining would itself have reactions on the monetary machine; and these would have further repercussions on the "real" process' ... 'But', he continues, 'perhaps the writer will be excused if he decides that, for the present, these repercussions lie outside the Theory of Wages' on the grounds that there is no general agreement among economists about the character of the reactions. But it is not possible to separate 'the real process' from 'its monetary reactions' in this way when we are dealing with all-round changes in wage-rates - even if it be possible when we are concerned with changes in a single occupation playing a small part in the total activity of the community. For in a monetary economy it is through the monetary mechanism that the effects of such a change are brought about, and their nature cannot be discovered or understood without a clear analysis of that mechanism: the monetary reactions, in fact, are not simply 'repercussions of' the process set up by the change, they are the process and must occupy a central position in the analysis of it. The only way to get rid of them is to postulate a barter-economy; and this Mr. Hicks does not do - his discussion hovers between what would happen in a barter economy and what does happen in a money-economy. He seems, for example, to suppose that monetary disturbances may be neglected if the wages fixed are supposed to be 'real wages' in the sense of 'money wages corrected for movements in the price-level of consumption goods' by means of 'cost of living sliding-scales' ... - which is manifestly untrue.

Thus, the obscurity and lack of precision which mar these chapters spring, I believe, from the attempt to narrow down the theory of wages by excluding from it any discussion, first, of the nature of capital and processes governing its supply, and, secondly, of the monetary reactions set up by changes, or disequilibria, in wage-rates." -- G. F. Shove, (1933). "Review of Hicks's The Theory of Wages, Economic Journal

See also:

• Molina, Mario Garcia (2005). "Capital Theory and the Origins of the Elasticity of Substitution (1932-35)", Cambridge Journal of Economics, V. 29: 423-437

Additions To Blog Roll

You might notice I recently added Chris Hayes and David Warsh to my blogroll. I may soon add Franklin Serrano to my blog roll. He describes his blog:

"The purpose of this blog is to be a forum for discussing political economy issues in the tradition of Piero Sraffa and Mikhail Kalecki."

I assume he'll be more policy-oriented than I am.

I've been thinking about saying something about Michel Kalecki myself, if only to document that it is a strawperson to say leftists imagine democratic governments will be run by altruistic idealist politicians looking out for the nation as a whole.

No One Can Repent And Will At Once; The Law of Contradiction Won't Allow It

Don Boudreaux confuses a shift in production functions - that is an innovation - with a choice among techniques in response to changes in relative factor prices. Not only that, he is simply incorrect about the analysis of the choice of technique.

Gabriel Mihalache also pretends that the logic of perfect competition with ideal rational behavior supports his exploded ideas about the minimum wage.

The Wretched of My Earth

I was born and raised in the Rochester metropolitian area. Long before I was born, the speech containing the following extract was delivered at Rochester:

"What to the American slave is your Fourth of July? I answer: a day that reveals to him, more than all other days in the year, the gross injustice and cruelty to which he is the constant victim. To him your celebration is a sham; your boasted liberty, an unholy licence; your national greatness, swelling vanity; your sounds of rejoicing are empty and heartless; your denunciation of tyrants, brass-fronted impudence; your shouts of liberty and equality, hollow mockery; your prayers and hymns, your sermons and thanksgivings, with all your religious parade and solemnity, are, to him, more bombast, fraud, deception, impiety and hypocrisy - a thin veil to cover up crimes which would disgrace a nation of savages...

...You boast of your love of liberty, your superior civilization, and your pure Christianity, while the whole political power of the nation (as embodied in the two great political parties) is solemnly pledged to support and perpetuate the enslavement of three millions of your countrymen. You hurl your anathemas at the crown-headed tyrants of Russia and Austri and pride yourselves on your democratic institutions, while you yourselves consent to be mere tools and bodyguards of the tyrants of Virginia and Carolina. You invite to your shores fugitives of oppression from abroad, honor them with banguets, greet them with ovations, cheer them, toast them, salute them, protect them, and pour out your money to them like wate; but the fugitive from your own land you advertise, hunt, arrest, shoot, and kill. You glory in your refinement and your universal education; yet you maintain a system as barbarous and dreadful as ever stained the character of a nation - a system begun in avarice, supported in pride, and perpetuated in cruelty. You shed tears over fallen Hungary, and make the sad story of her wrongs the theme of your poets, statesmen, and orators, till your gallant sons are ready to fly to arms to vindicate her cause against the oppressor; but in regard to the ten thousand wrongs of the American slave, you would enforce the strictest silence, and would hail him as an enemy of the nation who dares to make these wrongs the subject of public discourse!" -- Frederick Douglas, 5 July 1852

A Daniel Come To Judgement! Yea, A Daniel!

A blog post from a guest blogger at Glenn Greenwald's argues that Catholic teaching does not support some stances in opposition to an increase in the minimum wage in the United States. Catholic teaching on economic matters predates the establishment of capitalism. I happen to have recently read a claim by Alessandro Roncaglia that Pribram (1983) is a good scholarly work on medieval economics.

While I'm bringing attention to Catholic teaching on economics, I might as well mention some other texts. I don't claim to be authoritative on Catholic theology. These are just some texts I am aware of the existence of. Popes Leo XIII and Pius XI both issued encyclicals on the social question. I provide some quotes from a second Vatican Council document:

"...the picture is not without its disturbing elements. Many people, especially in economically advanced areas, seem to be dominated by economics; almost all of their personal and social lives are premeated with a kind of economic mentality, and this is true of nations that favor a collective economy as well as other nations. At the very time when economic progress (provided it is directed and organized in a reasonable and human way) could do so much to reduce social inequalities, it serves all too often to aggravate them; in some places it even leads to a decline in the position of the underprivileged and contempt for the poor. In the midst of vast numbers of people deprived of the absolute necessaries of life there are some who live in luxury and squander their wealth, and this happens in less developed areas as well. Luxury and misery exist side by side. While a few individuals enjoy an almost unlimited opportunity to choose for themselves, the vast majority have no chance whatever of exercising personal initiative and responsibility, and quite often they have to live and work in conditions unworthy of human beings...

...Justice and equity also demand that the livelihood of individuals and their families should not become insecure and precarious through a kind of mobility which is a necessary feature of developing economies. All kinds of discrimination in wages and working conditions should be avoided in regard to workers who come from other countries or areas and contribute by their work to the economic development of a people or a region. Furthermore, no one, especially public authorities, should treat them simply as mere tools of production rather than as persons; they should facilitate matters so that they may have their families with them and be able to acquire decent housing conditions, and they should endeavor to integrate them into the social life of the country or area to which they have come. However, employment should be found for them in their own countries whenever possible...

...we believe by faith that, through the homage of work offered to God, man is associated with the redemptive work of Jesus Christ whose labor with his hands at Nazareth greatly ennobled the dignity of work. This is the source of every man's duty to work faithfully, as well as the basis of his right to work; moreover, it is the duty of society, according to the prevailing circumstances, to see to it that all citizens have the opportunity of finding employment. Finally, renumeration for work should guarantee man the opportunity to provide a dignified livelihood for himself and his family on the material, social, cultural and spiritual level to correspond to the role and the productivity of each, the relevant economic factors in his employment, and the common good.

Since economic activity is, for the most part, the fruit of the collaboration of many men, it is unjust and inhuman to organize and direct it in such a way that some workers are exploited. But it frequently happens, even today, that workers are almost enslaved by the work they do. Under no circumstances can this fact be justified by so-called laws of economics. Therefore, the entire process of productive work must be adapted to the needs of the human person and to his way of life, with special attention to domestic life and mothers of families in particular, always taking sex and age into account. Workers should have the opportunity to develop their talents and their personality through the performance of their work. While devoting their time and energy to the performance of their work with a due sense of responsibility, they should also be allowed sufficient rest and leisure to cultivate their family, cultural, social and religious life. In addition, they should be given the opportunity to develop those energies and talents to which their professional work may perhaps give little scope...

...Among the fundamental rights of the individual must be numbered the right of workers to form themselves into associations which truly represent them and are able to cooperate in organizing economic life properly. Included is the right to freely take part in the activities of such associations without fear of reprisal..." - Paul VI (1965)

More parochially, Catholics in the United States can look to a U. S. Bishops' pastoral letter of two decades ago.

• Leo XIII (1891). Rerum Novarum
• Paul VI (1965). De Ecclesia in Mundo Huius Temporis
• Pius XI (1931). Quadragesimo Anno
• Pribram, K. (1983). A History of Economic Reasoning, Baltimore: John Hopkins University Press
• United States Catholic Conference (1986). Economic Justice for All: Pastoral Letter on Catholic Social Teaching and the U.S. Economy

A Post Keynesian Model of Growth and Distribution (Part 4 of 4)

3.0 SUMMARY

The previous three parts specify a steady-state growth model applicable to an advanced capitalist economy. Figure 2 summarizes the structure of this model. The arrows indicate how variables are determined, including accounting identities, in the mathematical structure of the model. Notice that the major macroeconomic variables are determined by decisions within the corporations. Household savings decisions can affect only the overall value of stocks and the personal distribution of income. Control over the means of production determines the functional distribution of income.

Figure 2: Dependencies Among Variables and Parameters

The above model is one of a family of models. Table 2 shows two important special cases in the development of this model. A generalization would assume saving propensities vary by source of income, as well as class.

Table 2: Variants

Variant	Characterization	Parameters
Kaldor (1966) variant	No class of pure capitalists	sr = 0, j = 1
Pasinetti (1962) variant	No corporate sector	sc = 0, f = 1, v = 1

A number of research programs can be organized around these models. The generalization of the production models to more commodities has been long accomplished. Kaldor also included endogenous technical change in his models. One might assume industries exhibit various barriers to entry. This is Paolo Sylos Labini's (old) Industrial Organization. The model shows the rate of industrial profits as depending on corporate decisions about growth and finance. Related issues are explored in managerial theories of the firm, as developed by Edith Penrose, Robin Marris, Adrian Wood, Alfred Eichner, and Edward Nell. I don't think this family of models is particularly strong on environmental issues; nevertheless, the extension of the production model to include joint production provides an essential tool for environmental economics. Some work has been done on including government and international trade in this family of models. Some have examined the relationship of this family of models to other theories of distribution, such as a monetary theory of distribution. One might see this theory as a long period extension of Keynes' General Theory. Kregel, who emphasizes the role of money and uncertainty have questioned whether such elements were adequately incorporated into this family of models. Man-Seop Park, building on and criticizing recent work by Thomas Palley, is investigating incorporating more elements of the financial system into this family of models. I do not claim the above brief survey is comprehensive.

REFERENCES

• Kahn, R. F. (1959). "Exercises in the Analysis of Growth", Oxford Economic Papers, New Series, V. 11: 143-156
• Kaldor, Nicholas (1956). "Alternative Theories of Distribution", Review of Economic Studies, V. XXIII: 83-100
• Kaldor, Nicholas (1966). "Marginal Productivity and the Macroeconomic Theories of Distribution: Comment on Samuelson and Modigliani", Review of Economic Studies, V. XXXIII, N. 4 (Oct.): 309-319
• Kregel, J. A. (1985). "Hamlet without the Prince: Cambridge Macroeconomics without Money", American Economic Review, V. 75, N. 2 (May): 133-139
• Moss, S. J. (1978). "The Post-Keynesian Theory of Income Distribution in the Corporate Economy", Australian Economic Papers, V. 17, N. 31 (Dec.):303-322
• Park, Man-Seop (2006). "The Financial System and the Pasinetti Theorem", Cambridge Journal of Economics, V. 30: 201-217
• Pasinetti, Luigi L. (1962). "Rate of Profit and Income Distribution in Relation to the Rate of Economic Growth", Review of Economic Studies, V. XXIX, N. 4 (Oct.): 267-279
• Robinson, Joan (1962). Essays in the Theory of Economic Growth, Macmillan

A Post Keynesian Model of Growth and Distribution (Part 3 of 4)

2.5 The Valuation Ratio, Dividends, Capital Gains, and the Interest Rate

The previous part describes the corporate sector in a model of steady-state growth. The first part introduces the model. This part extends the model to consider how financial institutions mediate household ownership of corporations.

The value of the capital goods owned by corporations is K. Households do not own these capital goods. Rather, they own stock. The market value of stock is (v K). The ratio of the market value of stock to the value of the capital goods used by corporations (the "book value") is known as the valuation ratio, v. I assume that the valuation ratio is constant along a steady-state growth path; variations in the valuation ration reflect short-term speculation.

The steady-state valuation ratio cannot be below unity. Otherwise, corporations would expand by purchasing financial assets, rather than capital goods. Since households typically do not buy blast-furnaces and other real capital goods, the valuation ratio can exceed unity.

Profits not retained by the corporate sector are paid out to households in the form of dividends. By assumption, dividends are (1 - sc)P. The increase in the value at the end of a year of the capital goods owned by corporations is net investment, I. The increase in the value of all shares is v I, while the value of new shares sold is f I. This latter quantity is needed to finance that portion of net investment not covered by retained profits. The difference in these quantities (v - f) I, is the value of capital gains.

Interest payments on financial capital are such that one consume them entirely and leave one's capital value unaltered. Thus, interest payments in this model are equivalent to the sum of dividends and capital gains. The rate of interest, i, is then defined by Equation 23:

(23)

Some algebraic manipulations and the definitions of the rate of profits and the rate of growth given by Equations 3 and 2, respectively, yield Equation 24:

(24)

Substituting from Equation 8, I obtain:

(25)

Or:

(26)

Assume that the rate of interest is greater than the rate of growth. Then, a valuation ratio greater than unity is equivalent to the rate of profits on industrial capital exceeding the rate of interest on financial capital along a steady state growth path.

2.6 Savings Decisions and Increases in Wealth

I assume the existence of a class of workers and a class of pure capitalists (rentiers) in the steady state. Members of both classes save, and therefore both obtain a share of profits. The rentiers obtain all their income from profits.

If both classes are to persist, the wealth of each class must grow at the steady-state growth rate, g. Equation 27 equates the rate of growth o rentier wealth:

(27)

where sr is the capitalists' (marginal and average) savings propensity and j is the proportion of stock owned by the workers. Equation 28 equates the steady-state rate of growth and the rate of growth of workers' wealth:

(28)

where sw is the workers' (marginal and average) savings propensity.

Equations 27 and 28 determine the valuation ratio and the proportion of stock owned by the workers. Some variables in these two equations have already been determined: wages, profits, net investment, and the value of capital. The rate of growth, the proportion of net investment financed by additional stock, the retention ratio, and the workers' and the capitalists' savings propensities of the model.

2.7 Parameter Ranges

Certain conditions must be met for a steady-state growth path to exist in the above model. Given a positive price of steel, Equation 29 follows from Equation 11:

(29)

Then the wage is positive if and only if:

(30)

Or:

(31)

By similar reasoning based on Equation 19, outputs of corn and steel are positive if and only if the inequality in Display 32 holds:

(32)

Displays 31 and 32 show a limit on the rate of profits and on the rate of growth. This limit is imposed by a parameter of the chosen technique. The inequality in Display 33 must hold for the rate of profits and the rate of growth to be positive:

(33)

The model imposes a necessary condition on savings propensities. Define sh as a weighted savings propensities over households:

(34)

Table 1 uses the household savings propensity to show the sources of savings. The first three rows show savings out of profits, while the last row shows savings from wages. Since intended savings equals investment along a steady-state path, Equation 35 must hold:

(35)

Or:

(36)

I assume both profit and wage shares are positive:

(37)

Display 38 gives a necessary condition to ensure positive shares for both classes:

(38)

This condition is that the savings rate out of wages be less than the sum of the proportion of retained earnings and the savings rate out of profits distributed as dividends.

Table 1: Sources Of Savings

Savings From Dividends	sh(1 - sc)P
Savings From Retained Earnings	sc P
Minus Consumption From Capital Gains	- (1 - sh)(v - f)I
Savings From Wages	sw(Y - P)

A Post Keynesian Model of Growth and Distribution (Part 2 of 4)

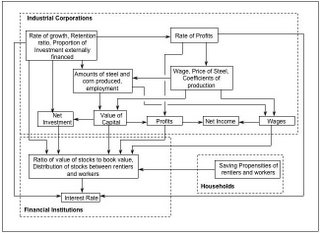
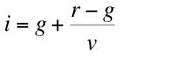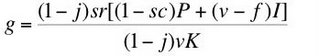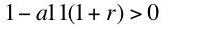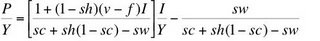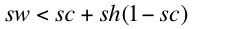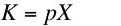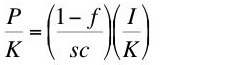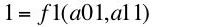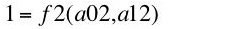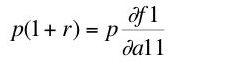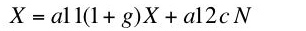2.0 THE MODEL

This part begins the exposition of the model introduced in the previous part. The exposition is organized into seven subsections in two parts. The first part, consisting of four subsections, describes the corporate sector. The two subsections at the beginning of the second part describe households and financial institutions. The last subsections describes some limitations on parameters that are necessary for the existence of a steady-state growth path in the model.

2.1 Some Accounting Identities

The corporations in this model economy, produce two commodities, steel and corn. Steel can be combined with labor to produce either more steel or corn. Corn is the consumption good. Steel is totally used up in the yearly production processes in the model. Thus, the output of the economy consists of steel to replace the steel used up in production, additional steel to support growth, and corn for consumption.

Let X represent tons steel used in a production cycle, and let p represent the price of steel. The value of capital, K, is given by Equation 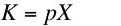1:

(1)

Let g be the steady-state rate of growth. Steel output, corn output, the employed labor force, and the value of capital all grow at this rate along a steady-state growth path. Thus, net investment, I, is related to the value of capital by Equation 2:

(2)

Equation 3 relates accounting profits, P, to the value of capital:

(3)

Equation 3 is a relationship characterizing the return to industrial capital. The returns to industrial capital and to financial instruments are distinguished in this model. It is convenient to follow tradition and refer to r as the rate of profits.

Let w be the wage, and let N be the number of employed person-years. Total wages, W, are then given by Equation 4:

(4)

There is no government and no foreign trade in this model. Net income, Y, is paid out in the form of wages and profits:

(5)

Equations 1 through 5 are basic identities in this model.

2.2 Finance and the Rate of Profits

The rate of growth is not determined within this model. It is the result of decisions by corporate managers, and it depends on their optimism or pessimism. In short, the rate of growth depends on the "animal spirits" of the corporate managers.

Investment has two sources of finance in the model, retained earnings and the issuing of new stock. Households purchase new stock in the model. Earnings that are not retained are paid out as dividends to stock owners. Let sc be the proportion of profits retained. Let f be the proportion of net investment financed by additional stock. Equation 6 follows:

(6)

Some algebraic manipulation yields Equation 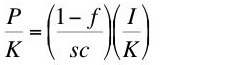7:

(7)

One obtains Equation 8 from Equations 2, 3, and 7:

(8)

Notice that all the parameters on the right-hand side of Equation 8 are controlled by corporate managers. Thus, the rate of profits on a steady-state growth path is the result of corporate decisions about the rate of growth and the financing of investment.

2.3 Production

Production occurs in the corporate sector. Firms producing steel face the technology defined by the production function in Equation 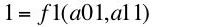9:

(9)

where a01 is the number of person years labor hired per ton steel produced, and a11 is the number of tons steel used as input per ton steel produced. The technology for producing corn is defined by the production function in Equation 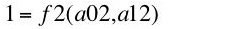10:

(10)

where a02 is the number of person years labor hired per bushel corn produced, and a12 is the number of tons steel used as input per bushel corn produced.

Production functions are assumed to exhibit Constant Returns to Scale and diminishing marginal returns. The inputs of steel are purchased at the start of the year, and the outputs of steel and corn become available at the end of the year. The corporations hire labor for use throughout the year and pay wages at the end of the year.

2.3.1 Price Equations

The same rate of profits is earned in each industry along a steady-state growth path:

(11)

(12)

Notice that corn is the numeraire in Equations 11 and 12, and relative prices are constant over time.

Given the coefficients of production, one can solve Equations 11 and 12 for the wage and the price of steel as a function of the rate of profits. Equation 13 gives the wage-rate of profits curve for the technique defined by a choice of the coefficients of production:

(13)

Equation 14 specifies the price of steel, given coefficients of production and the rate of profits:

(14)

The choice of technique can be analyzed by appending marginal productivity equations to either the system of equations given by Equations 11 and 12 or by Equations 13 and 14. Marginal conditions follow from assuming that competitive firms minimize cost, given technology. Alternatively, one can assume that competitive firms maximize economic profits. Equation 15 shows that the wage is equal to the value of the marginal product of labor in producing steel:

(15)

The wage is also equal to the value of the marginal product of labor in producing corn:

(16)

The price of steel, discounted to the end of the year when output becomes available, is equal to the value of the marginal product of steel used in producing steel:

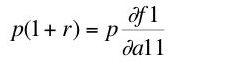(17)

Similarly, the discounted price of steel is equal to the value of the marginal product of steel in producing corn:

(18)

This analysis of the price equations shows that, given the rate of profits, coefficients of production, the wage, and prices of commodities are determined by cost-minimization. Notice no equation exists equating the marginal product of the value of capital, K, and the rate of profits. Marginal productivity conditions are part of the determination of the choice of technique. They do not determine distribution.

2.3.2 Quantity Equations

By assumption, X tons of steel and N person-years of labor are used as inputs in production in a single year. Since the rate of growth is g, (1 + g)X tons of steel are produced and available at the end of the year. Let c be the amount of corn produced per person-year. So c N is the amount of corn produced and available at the end of the year. Equation 19 equates the steel used as input to the sum of the steel inputs in the steel and corn industries:

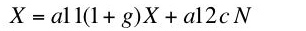(19)

Equation 20 equates the labor used as input to the sum of the labor inputs in the steel and corn industries:

(20)

One can solve Equations 19 and 20 for c and X/N as functions of the rate of growth and the coefficients of production. Equation 21 shows the trade-off between per-capita consumption and the rate of growth:

(21)

Notice this trade-off is of the same form as the wage-rate of profits curve (Equation 13). Steel per worker is given by Equation 22:

(22)

2.4 A Graphical Depiction of Elements of the Corporate Sector

This completes the analysis of the corporate sector. I have shown how, in this model, the rate of profit, the wage, prices, coefficients of production, and quantities produced per worker are determined. Figure 1 summarizes some of this discussion. The blue line in the fourth quandrant plots (the reflection of) Equation 8. In steady state growth, corporate managers have chosen the rate of growth, shown as g* on the abscissa. The corresponding steady state rate of profits, r*, is plotted downward on the ordinate. The graph shows this rate of profits reflected by the 45 degree line back onto the abscissa. The wage-rate of profits curves (Equation 13) for each technique are plotted in the first quadrant. Figure 1 shows two, while the marginal productivity relationships are applicable when an uncountable infinity of such curves exist. The coefficients of production for the chosen technique correspond to the highest wage-rate of profits curve for the rate of profits r*. The corresponding wage, w*, along a steady state growth path is plotted on the ordinate. Likewise, consumption per person-year is plotted on the ordinate by projecting the steady state rate of growth upward to the wage-rate of profits curve for the chosen technique.

Figure 1: Some Variables Dependent on the Rate of Growth

Postulate, say, an initial quantity of capital goods along a steady state growth path. The evolution of this quantity over time is specified, once the rate of growth is known. Equation 22 can be used to determine the time series for employment. Equation 14 can be used to determine the price of steel. Accounting identities can be used to calculate the value of capital (Equation 1), net investment (Equation 2), the distribution between profits (Equation 3) and wages (Equation 4), and net income (Equation 5). The distribution of income between persons requires an analysis of the financial sector and households. This analysis is provided in the next part.

A Post Keynesian Model of Growth and Distribution (Part 1 of 4)

1.0 INTRODUCTION

This series of posts presents a model in which an economy grows smoothly at a steady rate. The model postulates a certain institutional setting, namely advanced capitalism. Households save in this model by purchasing financial assets. They do not own individual capital goods to lend to firms. Corporations choose the rate of growth. In some sense, investment decisions are exogeneous or autonomous. Steady-state rates of growth are demand-constrained, not supply-constrained.

In Joan Robinson’s formulation, the purpose of this type of model is not to predict the future path of a capitalist economy. Rather, it is an analytical tool depicting necessary conditions for a smoothly growing capitalist economy under certain assumptions about institutions. In addition to the assumptions mentioned above, the model postulates that decision-makers follow certain rules of thumb or heuristics. This type of model can be used to assist one in identifying contradictions or aspects of capitalist economies that prevent smooth growth from being achieved from a current position.

The particular formulation of the model I present is unoriginal. I draw heavily on a paper by Scott Moss. This paper clarifies the logic of the inclusion of a corporate sector in this family of models. I deviate from Moss’ formulation in that I assume continuously differentiable microeconomic production functions, rather than fixed coefficients. I do this to emphasize the consistency of this model with marginal productivity, properly understood. The references I give at the end of the last post in this series are highly selective.

How To Argue Like A Reactionary

Suppose you want to argue knowledgeably about economics and political philosophy. Then the literature you should read seems unbounded. Here are three books I read years ago and still like:

• Hirschman, Albert O. (1991). The Rhetoric of Reaction: Perversity, Futility, Jeopardy
• Myrdal, Gunnar (1953). The Political Element in the Development of Economic Thought (Translated by Paul Streeten), Routledge and Kegan Paul
• Popper, Karl R. (1945). The Open Society and Its Enemies (Two volumes), George Routledge & Sons

Popper is relevant to the use of "utopian" as a pejorative. Utopias are "recipes for the cook-shops of the future", as Karl Marx put in his preface to the second edition of Capital. Marx and Engels famously opposed their "scientific socialism" to a prior utopian socialism. (See the first and second chapter of the third section of Anti-Dühring, also issued as a pamplet.) Popper, although opposed to so much of what he took Marx's approach to be, agreed with Marx in this. It is not the role of intellectuals to draw up blueprints for some ideal society and then to convince some actual country to adopt them. Plato, in his Republic, was misdirected. Popper thinks we should be trying to ameliorate existing evils, not globally remaking society or mandating happiness.

Myrdal writes a history of economics. He thinks one cannot correctly derive concrete policy proposals from abstract norms, such as "the greatest good for the greatest number". Nevertheless, political economists have often claimed to do exactly that. Myrdal critiques their argument.

Hirschman also writes a history. He explores how those on the right have argued against progressive policies. He identifies three main arguments rightists tend to pull out always:

• Perversity: attempts to improve matters will frustate themselves and only make matters worse. (Think of the incorrect neoclassical economics textbook argument about minimum wages.)
• Futility: the matters that we want to change are so deep seated that they cannot be reached, despite all our efforts.
• Jeopardy: We may be able to effect positive change, but we nevertheless put at risk other desirable features of society.

A slippery slope argument is a kind of jeopardy argument, I think. To express any skepticism about laissez-faire is not to advocate communism. But we are not presented with a choice between only government "non-intervention" and central planning as in no-longer-actually existing socialism.

Samuelson: "I Side With Sraffians"

"...One cannot match a proof like that of [the wage-interest rate frontier] by finding a valid proof for the stationary state conjecture [that consumption per head is not lower for a lower interest rate] (6). Why not? Because, as the next section will illustrate with numerical examples, such a conjecture is simply not true! ...

..Austrian novices and Nassau Senior's readers trumpet (in my paraphrase): 'Time itself is productive. Roundaboutness can be substituted for labor. The price of time is the interest rate. Aristotle, the Bible, the Koran, and St. Thomas Aquinas are wrong: competitive interest rate is not exploitation. The capitalist gets and needs to get the reward of positive interest rate. And to assuage him for his pains of (a) waiting to consume and (b) abstaining from eroding his capital by consuming more now rather than replacing the capital already in existence, he is properly being given part of the extra social product that his activity makes possible. It is a good bargain for the laborer: his wage product is fructified by what the capitalist provides as the real wage rate always rises when thrift and accumulation succeed in lowering the interest rate.'

But suppose time itself is not productive. Suppose the technical choices were between seven of labor two periods back and ten of labor three periods back. Incautious writings of Böhm's contemporaries declare, Humpty Dumpty-like: that is impossible; it contradicts a valid (a priori?) law of returns that more time means more product for the same total labor; read Jevons, read Böhm.

This is not cogent argumentation, as Hayek understands (1941, p. 60)...

...this defense does not validate an inverse [interest rate, consumption per worker] tradeoff in Equation (6) above. Adam Smith's Invisible Hand does ensure Equation (5) above but cares nought for Equation (6). This is why books entitled Economics in One Lesson must evoke from us the advice: 'Go back for the second lesson.'

Böhm was understandably tempted to say things like: 'Among the viable competitive time-phasing techniques, the technological law holds: Using more time, more roundaboutness, more complexity - when a lower interest rate motivates that competitively - must surely bring society a higher output from the same steady-state primary inputs of labor and land. Adam Smith's Invisible Hand must [sic] surely ensure that.'..

...in my dialogue with Sraffians, out of noblesse oblige I let them choose their weapons. By three well-chosen numerical examples, which Fisher (1907) might easily have fabricated, I side with Sraffians to show how and why there can be no universal measure of 'depth or duration of time-phased produced inputs' that can serve as simple apologetics for mainstream theories of interest. Unequivocal 'capital deepening' just cannot be defined...

...An economy's inventory of produced inputs is both complex and simple. Maintaining and improving upon congeries of productive inputs is an indispensible part of economic progress. All such time-phased processes will not evolve automatically: cave-people rose and fell in material well-being; eons passed without much cumulative change; great diversity of performance characterized geographically separated societies. Attempts to generalize simple family's or related-families' habit formation to large-group politics - a la utopian experimental cults or in the Lenin-Stalin and Mao pattern have not hitherto succeeded in organizing production with approximate Pareto-Optimality efficiency features. Gradual evolution toward near laissez-faire market mechanism responding to individual's self-interest, history suggests and advanced economic theory second guesses, will incur areas of market failure and will generate and perpetuate considerable degrees of economic and political inequalities. Just as there is no asymptotic communist utopia, neither is [there] an asymptotic laissez-faire utopia.

Böhm and Wicksell and Cassel and Wieser and Clark and Walras and Hayek and other economists before and after Sraffa, all must face what the role of intertemporal pricing must be in organizing technologies that are irreducibly time-phasing. When Joan Robinson and I discussed these matters face to face, I used to get nowhere with her by babbling about supply and demand. She already had seen through that tommy-rot. Things went better if I could keep the focus on Mao's China..." -- Paul Samuelson (2001). "A Modern Post-Mortem on Böhm's Capital Theory: Its Vital Normative Flaw Shared By Pre-Sraffian Mainstream Capital Theory". Journal of the History of Economic Thought V. 23, N. 3

Solow Japes

Robert Lucas changed the direction of mainstream macroeconomic research. David Warsh reminds me that Robert Solow is unhappy with this direction:

"Suppose somebody sits down where you are sitting now and announces to me that he is Napoleon Bonaparte. The last thing I want to do with him is to get involved in a technical discussion of cavalry tactics at the Battle of Austerlitz. If I do that, I'm getting tacitly drawn into the game that he is Napoleon Bonaparte." -- Robert M. Solow

I also like this quip:

"My impression is that the best and brightest in the profession proceed as if economics is the physics of society. There is a single valid model of the world. You could drop a modern economist from a time machine - a helicopter, maybe, like the one that drops the money - at any time, in any place, along with his or her personal computer; he or she could set up in business without even bothering to ask what time and which place. In a little while, the up-to-date economist will have maximized a familiar-looking present-value integral, made a few familiar log-linear approximations, and run the obligatory familiar regression. The familiar coefficients will be poorly determined, but about one-twentieth of them will be significant at the 5% level, and the other nineteen do not have to be published. With a little judicious selection here and there, it will turn out that the data are just barely consistent with your thesis advisor's hypothesis that money is neutral (or nonneutral, take your choice) everywhere and always, modulo an information asymmetry, don't worry, you'll think of one." -- Robert M. Solow (1984). "Economic History and Economics", Papers and Proceedings of the American Economic Association (Dec.): 330

Yes, Gabriel, He Must Be

Over on another blog, Gabriel Mihalache tries to cast doubt on econophysics:

"If Doyne Farmer thinks that there are systematic, exploitable, opportunities for profit... then he must be a very rich man, right?"

I turn to the Web site of the Prediction Company, where I find:

"Founded in 1991 by Doyne Farmer, Norman Packard and Jim McGill, Prediction Company quickly set out to take the financial world by storm. Based on their earlier work in chaos theory and complex systems Drs. Packard and Farmer felt the financial markets were an example of a highly complex system that would be amenable to predictive technology. They assembled a team of world class scientists and engineers to attack the problem.

In 1992 Prediction Company signed an exclusive five year deal to provide predictive signals and automated trading systems to O'Connor and Associates, a highly successful Chicago based derivatives trading firm. In 1994 O'Connor was purchased by Swiss Bank, one of the world's largest banks. Swiss Bank extended the exclusive relationship with Prediction Company for another two years. In 1998 Swiss bank and UBS merged to create the world's third largest financial institution. Prediction Company continues its ground breaking work with UBS AG, and in November, 2005, became a wholly-owned subsidiary of UBS AG."

References On Austrian Business Cycle Theory

In commenting on James' post, I mentioned I have already shown Austrian Business Cycle Theory to be false. If I ever revise this paper, I might want to make it shorter. I might also want to work in some additional references:

• Hayek, Friedrich A. (1941). The Pure Theory of Capital, Chicago: University of Chicago Press
• Kaldor, Nicholas (1942). "Professor Hayek and the Concertina-Effect", Economica, New Series, V. 9, N. 36 (Nov): 359-382
• Klausinger, Hansjörg (2006). "'In the Wilderness': Emigration and the Decline of the Austrian School", History of Political Economy, V. 38, N4: 617-664. See especially p. 650:

"...the book [Hayek 1941] could not achieve its aim, because of Hayek's lack of formal and mathematical skills and the impossibility of the task itself. [Footnote:] as taught by the outcome of the Cambridge capital controversies; for a retrospective view, see Samuelson 2001."

• Lachmann, L. M. (1940). "A Reconsideration of the Austrian Theory of Industrial Fluctuations", Economica, New Series, V. 7, N. 26 (May): 179-196
• Siven, Claes-Henric (2006). "Monetary Equilibrium", History of Political Economy, V. 38, N. 4: 665-709

Also, one of last two numbers in the 2006 volume of the Quarterly Journal of Austrian Economics is on the ABCT.

Adam Smith On An Information Asymmetry

I think I once read Michael Perelman pointing out this parallel between Smith and Stiglitz:

"...In a country, such as Great Britain, where money is lent to government at three per cent. and to private people upon good security at four, and four and a half, the present legal rate, five per cent., is perhaps as proper as any.

The legal rate, it is to be observed, though it ought to be somewhat above, ought not to be too much above the lowest market rate. If the legal rate of interest in Great Britain, for example, was fixed so high as eight or ten per cent., the greater part of the money which was to be lent, would be lent to prodigals and projectors, who alone would be willing to give this high interest. Sober people, who will give for the use of money no more than a part of what they are likely to make by the use of it, would not venture into the competition. A great part of the capital of the country would thus be kept out of the hands which were most likely to make a profitable and advantageous use of it, and thrown into the those which were most likely to waste and destroy it. Where the legal rate of interest, on the contrary, is fixed but a very little above the lowest market rate, sober people are universally preferred as borrowers to prodigals and projectors. The person who lends money gets nearly as much interest from the former as he dares to take from the latter, and his money is much safer in the hands of the one set of people, then in those of the other. A great part of the capital of the country is thus thrown into the hands in which it is most likely to be employed with advantage." -- Adam Smith, Wealth of Nations, Book II, Chapter IV

Gavin Kennedy titles his blog, "Adam Smith's Lost Legacy". So he must be only joking in this post when he whines about Stiglitz advocating government action to counter imperfections in information. (Kennedy also goes off, as right-wingers tend to do, with strawpersons and irrelevancies about the former Soviet Union.)