A Four-Technique Pattern

Figure 1: Partition of the Parameter Space

1.0 Introduction

I here provide some notes on a perturbation of an example from Salvadori and Steedman (1988).

Consider an economy in which n commodities are produced in n industries. In each industry, a single commodity is produced from inputs of labor and the services of previously produced capital goods. Suppose the technology can be represented in each industry by a continuously-differentiable production function. The wage-rate of profits frontier for such a model does not contain any switch points. In other words, for each feasible rate of profits, a single technique is cost minimizing. Nevertheless, the cost-minimizing technique varies continuously with the rate of profits. Furthermore, the process associated with the cost-minimizing technique in each industry also varies continuously with the rate of profits.

Suppose, instead, that the processes in each industry were represented by a set of fixed-coefficient processes, instead of a smooth production function. What would hold in a discrete model that is in the spirit of the neoclassical model? I suggest that at each switch point on the frontier, 2ⁿ wage curves would intersect. In a model with two produced commodities and two processes available in each industry, four wage curves would intersect at the single switch point. With three produced commodities, eight wage curves would intersect. The natural properties for a neoclassical model - if that is what this is - are flukes to several degrees.

I do not necessarily claim anything revelatory from the details of this post. I am testing the applicability of my pattern analysis by trying it out for various examples. Although you cannot tell from my presentation, the graphs I draw rely less on numerical approximations than in many of my earlier examples. This example is the first I have seen where a pattern with a co-dimension of two or higher happens to form a one-dimensional locus (curved line) in the two-dimensional slice of the parameter space I graph. Salvadori and Steedman could have varied their example in an infinite number of ways and still had an example where all processes varied at a switch point.

2.0 Technology

I make my usual assumptions about technology. At a given point in time, managers of firms know of a number of production processes (Table 1). A single commodity - a ton iron or a bushel corn in the example - is the output of each process. Each process lasts a year and exhibits constant returns to scale. Inputs are defined in physical units. For example, labor inputs are specified in terms of person-years per ton iron output or per bushel corn output. All inputs are used up in production; there is no fixed capital or joint production.

Table 1: The Technology for a Two-Industry Model

Input	Iron Industry		Corn Industry
	(a)	(b)	(c)	(d)
Labor	1 e1 - σ t	2 e1 - φ t	1	2
Iron	0	0	2/3	1/2
Corn	(2/3) e1 - σ t	(1/2) e1 - φ t	0	0

To produce a self-sustaining net output with this technology, both iron and corn must be produced. Four techniques can be defined with this technology (Table 2).

Table 2: Techniques in a Two-Commodity Model

Technique	Processes
Alpha	a, c
Beta	b, d
Gamma	a, d
Delta	b, c

I have defined the technology such that coefficients of production decrease with time in both processes for producing iron. The rate at which they decrease differs between the two processes. A more general case would allow for technical process in each of the processes for producing corn.

3.0 A Temporal Path

I first consider the variation with time of prices of production for a special case. Consider:

σ = φ = 1

I make the usual assumptions for prices. Relative spot prices are stationary, such that the same rate of profits is earned in both industries if the technology at a given point of time had prevailed over the year. I assume labor is advanced, and wages are paid out of the surplus at the end of the year. A bushel corn is taken as the numeraire. Supernormal profits cannot be made for either process comprising the chosen technique(s). No process in use incurs extra costs.

Figure 2 shows how cost-minimizing techniques, the maximum rate of profits, and switch points vary with time. In the region label 1, the Beta technique is cost-minimizing for all feasible rates of profits. The Gamma technique is cost-minimizing for high wages and low rates of profits in Reqion 2. A single switch arises, where wage curves for the Beta and Gamma techniques intersect on the frontier. In the language of the technical terminology I have been introducing, the boundary between Regions 1 and 2 is a pattern across the wage axis. Other patterns are labeled in the diagram.

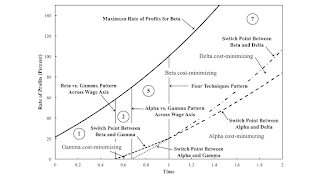
Figure 2: Variation of Switch Points with Time

When t = 1, this model reduces to Salvadori and Steedman's example. A single switch exists, with a rate of profits, r₀, of 20 percent and a wage of (1/5) bushel per person-year. The wage curves for all four techniques intersect at the switch point. I call the boundary between Regions 5 and 7 a four technique pattern.

I argue that a four technique pattern is of co-dimension two, in my jargon. Each pattern is defined for a switch point. So, in a pattern, at least two wage curves intersect at a switch point:

w_α(r₀) = w_γ(r₀)

The co-dimension is the number of additional conditions that must be satisfied for the pattern. Here are two more conditions:

w_β(r₀) = w_δ(r₀)

w_α(r₀) = w_β(r₀)

In this example, for any switch point between the Alpha and Beta techniques, all processes are cost-minimizing. Thus, all techniques are cost-minimizing at such a switch point. For any set of parameters (σ, φ, t) at which there exists a switch point on the frontier between Alpha and Gamma and between Beta and Delta, all techniques are cost-minimizing. In the example, the first two conditions imply the third because of the processes of which the techniques are composed. I think this implication does not hold in general, for all technologies. So I think the definition of a four technique pattern must include three equalities.

4.0 Partition of the Parameter Space

The above analysis can be generalized, to consider any combination of (σ t) and (φ t). Figure 1, at the top of the post, partitions the parameter space into seven regions. In any given region, the switch points and the wage curves along the frontier do not vary qualitatively. (Maximum wage, maximum rate of profits, and rate of profits for switch points may vary.) Table 3 lists the switch points and wage curves along the wage frontier, for each region.

Table 3: Cost-Minimizing Techniques

Region	Switch Points	Techniques
1	None	Beta
2	Between Beta & Gamma	Gamma, Beta
3	None	Gamma
4	Alpha & Gamma	Alpha, Gamma
5	Alpha & Gamma, Beta & Gamma	Alpha, Gamma, Beta
6	Beta & Delta	Delta, Beta
7	Alpha & Delta, Beta& Delta	Alpha, Delta, Beta

As an aid to visualization, I present some specific configuration of wage curves. Consider the point in the parameter space that is simultaneously on the boundary of Regions 1, 2, 5, 6, and 7. At this point, all techniques are cost-minimizing for a rate of profits of zero. It is simultaneously a four-technique pattern and patterns across the wage axis. Figure 3 shows the wage curves in this case. For feasible positive rates of profits, the Beta technique is uniquely cost-minimizing.

Figure 3: Patterns over the Wage Axis

Figure 1 shows loci for four wage patterns intersecting at the point in the parameter space with wage curves illustrated above. Since six pairs of (unordered) techniques can be chosen from four techniques, one might think that six wage patterns should intersect at this point. But I am only defining patterns for switch points on the frontier. To illustrate, consider figure 4, which shows wage curves for a point in Region 5. The wage curves for the Gamma and Delta techniques intersect on the wage axis. Neither, however, are cost-minimizing here; the Alpha technique is cost-minimizing for a rate of profits of zero.

Figure 4: Wage Frontier in Region 5

Region 7 is the other region in three techniques are cost-minizing along the wage frontier. Figure 5 illustrates Region 7. For this particular set of parameters, the wage curves for the Gamma and Delta techniques are tangent at a point within the wage frontier. As far as I can tell, no reswitching patterns arise in this example, for switch points on the frontier.

Figure 5: Wage Frontier in Region 7

It is also the case that if one extends Figure 1 to the right, the locus for the four-technique pattern never ends. There is not some set of parameter values where the wage curves for all techniques intersect at the maximum rate of profits.

In a perturbation of the example, one can find a set of parameters at which the wage curves for all four techniques intersect at a switch point for a rate of profits of zero. And the parameters can be varied such that the rate of profits for a switch point for all four techniques can be any positive rate of profits.

Reference

• Salvadori, Neri and Ian Steedman. 1988. No Reswitching? No Switching! Cambridge Journal of Economics, 12: 481-486.

From Odo's Prison Letters

For we each of us deserve everything, every luxury that was ever piled in the tombs of the dead kings, and we each of us deserve nothing, not a mouthful of bread in hunger. Have we not eaten while another starved? Will you punish us for that? Will you reward us for the virtue of starving while others ate? No man earns punishment, no man earns reward. Free your mind of the idea of deserving, the idea of earning, and you will begin to be able to think. -- Ursula K. Le Guin (21 October 1929 - 22 January 2018)

Labor Values Taken As Given

I have been considering a case in which a simple Labor Theory of Value (LTV) is a valid theory of prices of production. When, for each technique, all processes have the same organic composition of capital, prices of production are proportional to labor values. Given labor values and direct labor coefficients in each industry, an uncountably infinite number of techniques - as specified by a Leontief input-output specified in terms of physical inputs per physical outputs - satisfies these conditions.

In outlining this mathematics, I start with labor values and derive technical conditions of production as a detour on the way to prices of production. (I have also considered a perturbation of this possibility, as an application of my pattern analysis.)

Has anybody commenting on Marx actually started with labor values, taken as given, in this way? If this is a straw person, I am good company. Ian Steedman (1977) makes something like the same accusation. See the section, "A spurious impression", in Chapter 4, "Value, Price, and Profit Further Considered", of his book.

But I have found examples of other approaching Marx in something like this way. I refer to von Bortkiewicz (1907) and Seton (1957), two authors taken as a precursor to the Sraffian reading of Marx. The fact that Steedman can be read as criticizing such authors complicates the claim that this literature exhibits continuity. I think others have also argued that some novelty arises in Steedman's critique insofar as he argues that labor values are redundant, since prices of production are properly calculated from technical data on production and the physical composition of wage goods.

Perhaps my examples of Bortkiewicz and Seton should not be read as propounding any large claim that Marx takes labor values as more fundamental, in some sense, than physical conditions in production processes. Rather, Bortkiewicz started from the schemes of simple and expanded reproduction at the end of Volume 2 of Capital. Since Seton, and other authors, were generalizing and commenting on Bortkiewicz, they, as a matter of path dependence, happened to keep the assumption of given labor values. One wanting to argue for a reading of Marx that I seem to be stumbling into, without any firm commitment, needs to deal with Volume 1.

I have two additional notes on rereading these references. First, I like to talk about Marx' invariants in the transformation problem. I thought I had taken this term from formal modeling in computer science. Edsger Dijkstra and C. A. R. Hoare talk about loop invariants, and I sometimes even comment my code with explicit statements of invariants. But Seton has a section titled "Postulates of Invariance".

Is Steedman disappointed in the reception of his book? Obviously, his points about the transformation problem, including the possibility of negative surplus value being consist with positive profits, under a case of joint production, have been widely discussed. But consider his exposition of simple examples intended to demonstrate that Sraffa's analysis can take into account all sorts of issues that some had argued were ignored. Consider letting how much work capitalists can get out of labor being a variable, heterogeneous types of abstract labor not reducible to one and the possibility of workers of each type exploiting others, wages being paid, say, weekly, during processes that take a year to complete, how wages relate to the rate of exploitation when a choice of technique exists, the treatment depreciation of capital, and the existence of a retail sector for circulating produced commodities. How many of these analyses have been taken up and continued by those building on Sraffa? (I think some have.)

References

• Eugen von Bohm-Bawerk (1949). Karl Marx and the Close of his System: Bohm-Bawerk's Criticism of Marx. Edited by P. M. Sweezy.
• Ladislaus von Bortkiewicz (1907). On the Correction of Marx's Fundamental Theoretical Construction in Third Volume of Capital, Trans. by P. M. Sweezy. In Bohm-Bawer (1949).
• F. Seton (1957). The "Transformation" Problem. Review of Economic Studies, 24 (3): 149-160.
• Ian Steedman (1981, first edition 1977). Marx After Sraffa, Verso.

Start of a Catalogue of Flukes of Fluke Switch Points

I claim that the pattern analysis I have defined can be used to generate additional fluke switch points. I am particularly interested in switch points that are flukes in more than one way (local patterns of co-dimension higher than one) and fluke switch points that are combined with other fluke switch points or some aspect of other switch points (global patterns). I have already generated some examples, not always with pattern analysis.

• Fluke switch points of higher co-dimension
• A switch point that is simultaneously a pattern across the wage axis and a reswitching pattern (a case of a real Wicksell effect of zero).
• A switch point combining four three-technique patterns (due to Salvadori and Steedman).
• Fluke switch points combined with other switch points
• A reswitching example with one switch point being a pattern across the wage axis (another case of a real Wicksell effect of zero).
• An example with a pattern across the wage axis and a pattern over the axis for the rate of profits.
• Two switch points with both being reswitching patterns can be found from a partition of a parameter space where two loci for reswitching patterns intersect.
• A pattern across the point where the rate of profits is negative one hundred percent, combined with a switch point, for the same techniques, with a positive rate of profits (of interest for the reverse substitution of labor).
• An example where every point on the frontier is a switch point.

The above list is not complete. More types of fluke switch points exist. Some, like the examples of a real Wicksell effect of zero, I thought, should be of interest for themselves to economists. Others show examples of parameters where the appearance of the wage frontier, at least, changes with perturbations of the parameters. I would like to see that in at least some cases, short run dynamics changes qualitatively with such perturbations. But this seems to be beyond my capabilities.

Maybe I'll update this post some day, if I create more examples.

A Pattern For The Reverse Substitution Of Labor

Figure 1: Variation of Switch Points with Time

1.0 Introduction

This post presents another local pattern of co-dimension one. I have conjectured that only four types of local patterns of co-dimension one exist (a reswitching pattern, a three-technique pattern, a pattern across the wage axis, and a pattern over the axis for the rate of profits). In this conjecture, I meant to implicitly limit the rate of profits at which switch points occur to be non-negative and not exceeding the maximum rate of profits. The pattern illustrated in this post is a pattern around the rate of profits of -100 percent. (I was prompted to develop this example by an anonymous comment, as I was also prompted for this post.)

Although this is a local pattern, its interest comes from global effects. Suppose another switch point exists, other than the one at a rate of profits of -100 percent. This other switch point involves the same two techniques and occurs at a positive rate of profits. A perturbation of coefficients of production around the pattern changes the other switch point from one exhibiting a conventional substitution of labor to the reverse substitution of labor. Han and Schefold (2005) describe empirical examples of the reverse substition of labor.

2.0 Technology

Table 1 specifies the technology for this example. I make the usual assumptions. Each column lists inputs per unit output for each process. Each process exhibits constant returns to scale. Each process requires a year to complete, and there are no joint products. Inputs of capital goods are totally used up in production.

Table 1: Processes of Production

Input	Iron Industry	Corn Industry
		Alpha	Beta
Labor	1 Person-Yr.	9/10	0.994653826 e-σ t
Iron	(7/10) Ton	1/40	0.002444903 e-σ t
Corn	2 Bushels	1/10	0.746512055 e-σ t

In this example, technical change occurs in the Beta process for producing corn. I assume that σ is 1/10. So coefficients of production fall at a rate of ten percent.

At any moment of time, two techniques can be created out of these processes. The Alpha technique consists of the iron-producing process and the corn-producing process labeled Alpha. Likewise, the Beta technique consists of the iron-producing process and the corn-producing process labeled Beta.

3.0 Prices and Structural Economic Dynamics

I consider a common system for defining prices of production. Relative spot prices are assumed to be constant, and the same rate of profits is earned in both industries for the cost-minimizing technique. Labor power is advanced, and wages are paid out of the surplus product at the end of the year. For a technique that is not cost-minimizing, the costs for operating the corn-producing process in this technique, as evaluated at prices of production, exceed the revenues. I take a bushel corn as the numeraire.

These assumptions allow one to construct wage curves for each technique. The cost-minimizing technique at, say, a given rate of profits is found from the outer envelopes of the wage curves, that is, the wage frontier. Switch points arise at rate of profits for which both techniques are cost-minimizing. For this example, I do not present wage curves at selected moments of time. Figure 1 graphs the rate of profits at switch points and the maximum rate of profits against time. Patterns, including a pattern for the reverse substitution of labor, are indicated on the graph.

3.1 A Superficial Neoclassical Story

Suppose one limits one's analysis to non-negative rates of profits. Figure 1 shows that technical progress leads to a switch point at the maximum rate of profits. As the wage curve for the Beta technique continues to move outward, this switch point falls below the maximum rate of profits. For rate of profits lower than at the switch point, the Alpha technique is cost-minimizing. The Beta technique is cost-minimizing at higher rates of profits. Eventually, the switch point disappears across the wage axis, and only the Beta technique is cost-minimizing.

This story initially seems to correspond to exploded neoclassical intuition about technical change. Reswitching and capital-reversing - two phenomena much emphasized in the Cambridge Capital Controversy - never occur. Around the switch point with a positive rate of profits, the Beta technique is cost-minimizing at a notionally smaller wage, and the Alpha technique is cost-minimizing at a notionally higher wage. A lower wage is associated with a technique in which greater labor inputs, aggregated across both industries, are employed per bushel of corn produced net.

3.2 A Region in which the Reverse Substitution of Labor Occurs

But consider what happens when the analysis is extended to a rate of profits of -100 percent. A switch point with a positive rate of profits exists only for time between the patterns over the axis for the rate of profits and across the wage axis. Figure 2 graphs the difference in the labor coefficients with time. After the pattern for the reverse substitution of labor, the labor coefficient for the Alpha process in producing corn exceeds the labor coefficient for the Beta process in producing corn. That is, around the switch point, the adoption of the cost-minimizing technique at a lower wage results in less labor being employed in corn production per unit corn produced gross. How is this consistent with the textbook account of labor demand functions?

Figure 2: Change in Labor Input per Unit Gross Output in Corn

4.0 Conclusion

The more I investigate price theory, the less I understand how economists can teach neoclassical microeconomics.

Labor Values As A Foundation

Figure 1: Physical Production Data as a Side Route

1.0 Introduction

One way of reading the first volume of Marx's Capital is that labor values provide a foundation, upon which the structure of prices of production and, eventually market prices are based. I find that, for example, Joseph Schumpeter presents Marx's work in this way.

Another reading takes both labor values and prices as founded on physical data specifying the technique in use. Ian Steedman, as illustrated in Figure 2, argues for such a reading. Furthermore, Steedman argues that one cannot get from the system of labor values to prices. Labor values are not needed for analyzing prices of production; they are redundant.

Figure 2: Labor Values as a Side Route

These are not the only possible ways of reading Marx. Another reading might emphasize the bits on commodity fetishism. Nothing is hidden. In selling produced commodities on the market, the concrete work activities that go into making commodities are abstracted from and treated as commensurable. This is crazy, but according to Marx, this is how capitalism works.

I seem to have stumbled on some mathematics supporting the first reading. I consider the question of what physical data is consistent with given labor values and direct labor inputs, under the condition that the organic composition of capital does not vary among industries. The issue is not that there is no way to go from labor values, through data on physical production, to prices. Rather, there are too many routes - in fact, an infinite number of them.

Figure 1 is not quite how I present my results in my draft paper. I end up with the wage curve for the price system; unlike in the above diagram, I do not close the system. I am not sure I am correct on how I specify distributive variables in the figure. I end up with the wage as a vector, where the same money wage is earned in each industry. I found it natural to close the system with the rate of profits when going from labor values to prices. On the other hand, I found it more convenient to specify the wage in going from physical data to prices. Perhaps these closures need more thought.

A substantial issue is whether it makes any sense to talk about labor values prior to and independently of physical data on processes of production. Steedman asserts it is not possible. Marx, in the first volume of Capital goes back and forth between labor values and prices. I might need to think a little more about how money, or the choice of a numeraire, fits into this, but I seem to be arguing for this possibility, at least under the conditions in which a simple labor theory of value holds as a theory of price.