|
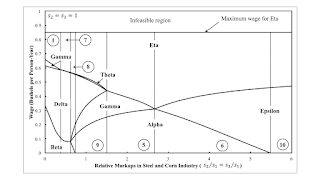
| Figure 1: Variation in the Maximum Wage and the Cost-Minimizing Technique with Time |
1.0 Introduction
I thought I would revisit the application of my analysis of fluke switch points to an example of Harrod-neutral
technical change. Two techniques are assumed to experience Harrod-neutral technical change. The same commodities
are produced with both techniques. No capital goods are produced for one technique that
are unproduced in the other. Consequently, the techniques have no processes in common. At least two processes
must be available in each industry. So more than two techniques must exist.
I think these ideas could be worked up into something. I will probably spend some time toying with the
example.
2.0 Technology
This economy produces a single consumption good, called corn. Corn is also a capital good, that is, a produced commodity used in
the production of other commodities. In fact, iron, steel, and corn are capital goods in this example. So three industries exist. One
produces iron, another produces steel, and the last produces corn. Two processes exist in each industry for producing the output of
that industry. Each process exhibits Constant Returns to Scale (CRS) and is characterized by coefficients of production.
Coefficients of production (Table 1) specify the physical quantities of inputs required to produce a unit output in the
specified industry. All processes require a year to complete, and the inputs of iron, steel, and corn are all consumed over the
year in providing their services so as to yield output at the end of the year. The technology is specified for a specific
moment in time, and improves over time.
Table 1: The Technology
| Input | Iron
Industry | Steel
Industry | Corn
Industry |
| a | b | c | d | e | f |
| Labor | (15/2) e-φt | 32 e-σt | (13/2) e-φt | 60 e-σt | (15/2) e-φt | 55 e-σt |
| Iron | 1/6 | 2/5 | 1/200 | 1/100 | 1 | 0 |
| Steel | 1/200 | 1/400 | 1/4 | 3/10 | 0 | 1/4 |
| Corn | 1/300 | 1/300 | 1/300 | 0 | 0 | 0 |
A technique consists of a process in each industry. Table 2 specifies the eight techniques that can be formed from the processes specified by the technology. If you work through this example, you will find that to produce a net output of one bushel corn, inputs of iron, steel, and corn all need to be produced to reproduce the capital goods used up in producing that bushel.
Table 2: Techniques
| Technique | Processes |
| Alpha | a, c, e |
| Beta | a, c, f |
| Gamma | a, d, e |
| Delta | a, d, f |
| Epsilon | b, c, e |
| Zeta | b, c, f |
| Eta | b, d, e |
| Theta | b, d, f |
The Alpha and Theta techniques each undergo Harrod-neutral technical progress. The labor
coefficients for the Alpha technique decrease at the the rate φ and those for the
Theta technique decrease at the rate σ. The other techniques consist of a mixture
of processes from these two techniques.
3.0 Prices of Production
A system of equations can be set out for prices of production, for each technique,at any moment of time.
I assume that net output consists of a bushel corn, and that this net output is
the numeraire. Wages are paid out of the surplus product after the harvest.
Given competitive conditions, the same rate of profits are obtained in each industry.
These assumptions are sufficient to determine the wage and the prices of produced commodities,
for each technique, at the given moment in time, as a function of the rate of profits.
4.0 The Choice of Technique
The cost-minimizing technique at a moment of time can be found by constructing the wage frontier
as the outer envelope of the wage curves for the eight techniques. Given the rate of profits,
the cost-minimizing technique maximizes the wage. Given the wage, it maximizes the rate of profits.
Figure 1, at the top of this post, and Figure 2 depict how the dependence of the cost-minimizing
technique on distribution varies with time. These graphs are drawn for the indicated rates of neutral technical progress
in the Alpha and Theta techniques.
Figure 1 graphs the maximum wage and the wage at each
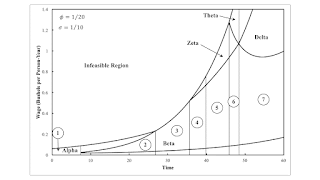
switch point on the frontier. Figure 2 graphs the rate of profits, both the maximum and at each
switch point on the frontier. Figure 2 also shows the rate of profits at switch points between -100
percent and zero. The thin vertical lines partition time into numbered regions. Each partition
corresponds to a fluke switch point.
|
| Figure 2: Variation in the Maximum Rate of Profits and the Cost-Minimizing Technique with Time |
The ranking of techniques by the maximum rate of profits does not vary with time.
At the maximum rate of profits, the wage is zero. Variations in labor coefficients do not matter.
In this case, the Alpha technique
remains cost-minimizing for all time at a wage of zero.
It is not necessary, in general, that the cost-minimizing technique at a zero wage, be one of those experiencing
Harrod-neutral technical change. For other coefficients of production, the Beta technique, for example, could be cost-minimizing
at a zero wage.
In general, the cost-minimizing technique at the maximum wage starts with the technique with the slowest rate
of neutral technical progress. Over time, the cost-minimizing technique becomes the technique with the largest rate
of technical progress.
In the example,
the Alpha technique is cost-minimizing at the start of time, whatever the distribution of income. Region 1 illustrates
this lack of dependence of the cost-minimizing technique on distribution.
the Alpha technique
remains cost-minimizing for all time at a wage of zero. Since the rate of Harrod-neutral technical progress is assumed to
be greater for the Theta technique, eventually Theta is cost-minimizing at the maximum wage. One can see the effects
of technical progress with the exponential growth of the maximum wage in Figure 2.
Consider Region 7 in the Figures. At a non-fluke switch point, only one process changes in the cost-minimizing technique.
As the wage increases, the corn-producing process changes at the switch point between Alpha and Beta. At the second switch-point
with increasing wages, the cost-minimizing process in steel production changes. Finally, at the switch point between Delta
and Theta, the cost-minimizing process in in iron production changes.
In Region 6, which process changes first, with increasing wages, in iron and steel production varies. The iron
process varies at the switch point between Beta and Zeta. At a higher wage, the steel process in the cost-minimizing
technique varies at the switch point between Zeta and Theta. The partition between Region 6 and Region 7 has a
fluke switch point in which the iron and steel-producing processes change simultaneously.
Region 2 exhibits reswitching between the Alpha and Beta techniques. The switch point at the lower wage is an
example of capital-reversing, also known as a positive real Wicksell effect. Around this switch point, a higher
wage is associated with the employment of more labor per unit of net output. It also exhibits the reverse
substitution of labor. In Regions 2, 3, and 4, the labor coefficient in Process f exceeds the labor
coefficient in Process e. A higher wage at this switch point between Alpha and Beta is associated
with greater employment per unit of gross corn output.
5.0 Conclusion
The introduction of switch points and the variation in the cost-minimizing technique at the maximum
wage is, in some sense, a general property of technology formed out of techniques experiencing Harrod-neutral
technical progress.
With time, switch points are introduced as fluke cases. These fluke cases need not create examples of
reswitching, capital-reversing, reverse labor substitution, or process recurrence.
But they do in the example.