Elsewhere

• Samuel Bowles on how "Marx’s representation of the power relationship between capital and labour in the firm is an essential insight"
• Economics in the Rear-View Mirror on renewal of Paul Sweezy's instructorship.
• Manoucher Parvin, in 1992, asks, "Is teaching neoclassical economics as the science of economics moral?"
• Alexander Douglas on micro-founded macro.
• A review of Fredric Jameson's new book, in Jacobin earlier this month.
• A review of Fredric Jameson's new book, in the September issue of Harper's.

The Production Of Commodities And The Structure Of Production: An Example

Figure 1: Wage Curves for the Two Techniques

1.0 Introduction

Economists following the Austrian school often represent the structure of production with Hayekian triangles (Hayek 1931, Rothbard 1962, Skousen 1990, Garrison 2001, Machaj 2017). Typically, goods of the highest order are produced with unaided labor or other unproduced original resources. (Fillieule (2007), in which a Hayekian triangle is constructed with an infinite stream of unproduced inputs, is an exception.) Rarely, is a model of the production of commodities by means of commodities, as in Sraffa (1960), considered. This post illustrates how to construct a Hayekian triangle with such a model, in the case with circulating capital.

It also illustrates how the use of such triangles to tell the stories that Austrian economists want to tell cannot be sustained.

This post uses one special case to consider another. A model of the production of commodities with only circulating capital and one original factor of production, labor, is used to examine Hayekian triangles, which cannot be rigorously constructed in more general cases (Hayek 1941). This approach is consistent with the research strategy recommended by Harwick (2022). Harwick's argues that capital theory needs to consider exemplary special cases, not begin with the most general case. Here, the most general cases would be general joint production and flow-input, flow-output models. (Hayek 1941 seems to be the source for the classification of inputs as point input or flow input and outputs as point output or flow output.)

Other approaches to capital theory by economists following the Austrian school, such as the use of the financial measure of Duration by Lewin & Cachanosky (2021), are not treated in this post. Fratini (2019) criticizes this financial approach, approach based on reswitching.

2.0 Technology and Net Output

Suppose technology is as characterized by the coefficients of production in Table 1. All techniques are characterized by single production, no fixed capital, and no joint production. In the Alpha technique, the first corn-producing process is operated. The second corn-producing process is operated in the Beta technique. The ale-producing process is operated in both techniques.

Table 1: Regions

Input	Corn Industry		Ale Industry
	Process I	Process II	Process III
Labor	1 person-yr.	275/464 person-yrs.	1 person-yr.
Corn	1/10 kilo-bushels	113/232 kilo-bushels	2 kilo-bushels
Ale	1/40 kilo-liters	1/800 kilo-liters	2/5 kilo-liters
OUTPUTS	1 kilo-bushel	1 kilo-bushel	1 kilo-liter

Each column in the Leontief matrix and corresponding direct labor coefficient defines a production process. Each process exhibits constant returns to scale and requires a year to complete. Each of the produced commodities are available at the end of the year. All commodities enter, either directly or indirectly, into the production of all commodities and the economy is productive. Labor is directly required to operate each process.

This analysis takes the proportions in the net product as given. These proportions are specified by a column vector, as in Table 2. This numeraire is the net product or net output of Sraffa's standard system for the Alpha technique. This special case has implications for the shape of Hayekian triangles, as seen below.

Table 2: The Numeraire

Commodity	Amount
Corn	d1 = (337 - 29 (29)1/2)/455 kilo-bushels
Ale	d2 = (17 + 25 (29)1/2)/1,820 kilo-kiters

The capital goods required as inputs are found by solving the model. The money supply is here assumed to adjust as needed. The construction of a traverse from one equilibrium to another is a difficult question. In a disequilibrium process, one would need to consider disappointed expectations and inconsistent plans, for example. Mainstream economists have a theory of non-steady state equilibrium paths. Rosser (1983) argues that reswitching manifests as a cusp catastrophe in this theory. Gram & Harcourt (2017) note some issues raised by taking the theory of equilibrium paths as an answer to the reswitching controversy. In the theory, any time to get into equilibrium is too long.

The numeric example is constructed on the basis of the following assumptions, in addition to those already given for characterizing the available technology:

• Stationary states are compared.
• Only one original factor of production, labor, is used.
• One person-year is employed. More generally, full employment is assumed, with a given size of the labor force.
• Wages are paid at the end of the year, not advanced with the payments for capital goods at the beginning of the year.

Hayekian triangles cannot be constructed under the more general assumptions of Hayek (1941).

3.0 Price Systems

Prices and distribution are specified with one degree of freedom, by a given technique. Prices must satisfy the following equations, given the technique, for the same rate of profits to be obtained in both industries:

(p₁ a_1,1 + p₂ a_2,1)(1 + r) + w a_{0, 1} = p₁

(p₁ a_1,2 + p₂ a_2,2)(1 + r) + w a_{0, 2} = p₂

The following equation follows from the definition of the numeraire.

p₁ d₁ + p₂ d₂ = 1

Adam Smith called these prices 'natural prices'. David Ricardo called them 'prices of production'. Alfred Marshall called them 'normal prices'. At any rate, they define the appropriate price system for an economy in a synchronized state, as in this thought experiment.

The model in this article is open. Distribution, including the wage and the interest rate, are not determined. Dumenil & Levy (1985) present a model in which workers consume their entire wage and the interest rate varies with shifts in the capitalists' utility functions. Marglin (1984) also presents a model with intertemporal utility maximization, as well as non-neoclassical ways of closing the model. Closures with intertemporal utility maximization can explain how the interest rate varies. Multiple equilibria can arise in such models.

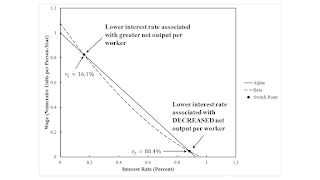
Figure 1 shows the wage curves for the two techniques. The choice of the numeraire results in the wage curve for the Alpha technique being a straight line, that is, an affine function. Look at the intercepts on the abscissa. The maximum rate of profits for the Beta technique exceeds the maximum for the Alpha technique. On the other hand, the intercepts on the ordinate show that net output per worker for the Beta technique exceeds the net output per worker for the Alpha technique. If the curvature for the wage curve for the Beta technique were concave to the origin, these properties of the intercepts would be reversed in a reswitching example.

The analysis of the choice of technique, in the circulating capital case, does not rely on the construction of the so-called factor price frontier. Milano (2024) notes that this is a misleading name for the wage frontier in Figure 1. Rather, this analysis has an algorithmic justification in the analysis of prices of production (Bharadwaj 1970, Woods 1990, Bidard 1990, Vienneau 2005 and 2017). Bidard & Klimovsky (2004) that the analysis based on the wage frontier does not necessarily extend to general joint production. Specific analyses have been developed for special cases of joint production, notably in the case of fixed capital and of extensive and intensive rent (Pasinetti 1980).

Figure 2 illustrates another analysis of the cost-minimizing technique. The left-hand side is constructed with prices for the Alpha technique, while the right-hand side illustrates prices for the Beta technique. One can see that greater profits are obtained, at low and high rates of profits, by adopting the second corn-producing process at Alpha prices. Likewise greater profits are obtained, at intermediate rates of profits, by adopting the first corn-producing process at Beta prices. Thus, the cost-minimizing technique, at a given interest rate, is the technique contributing its wage curve to the outer frontier at that interest rate.

Figure 2: Extra Profits for Price Systems

This example can be used to explore two parables, what one might call a neoclassical and a Austrian story:

• A lower interest rate incentivizes managers of firms to adopt a more capital-intensive technique. With more capital per worker, the steady-state net output per worker is higher.
• A lower time preference results in a willingness to defer consumption and a lower interest rate. This lower time preference is seen in the support of a longer structure of production and less consumption per worker.

The second switch point demonstrates that the first story is ill-founded. The construction of Hayekian triangles below demonstrates the second story is ill-founded. The example does demonstrate that the second story is not refuted merely by objections to the first.

4.0 Perverse Hayekian Triangles at the First Switch Point

In a previous post, I showed how to find the labor used to produce net output, in the current and each future year, when production is synchronized in a given year.

The increment in each step, for a given technique, is the value added by the original factors of production in that step. That is, an increment is the product of the wage and the labor for that order of goods, properly costed up with interest charges.

Figures 3 and 4 display the Hayekian triangles at the first switch point. The ordinate is the order of goods, as in Menger (187?). The abscissa is the value of the goods of that order that ultimately go into producing consumption goods, that is, goods of the first order. The length of the first step is the intersection of the corresponding wage curve with the ordinate in Figure 1. The increments in the steps are the values added by original, unproduced factors of production. In this case, labor is the only original factor of production.

Figure 3: Hayekian Triangle at First Switch Point

Figure 4: Hayekian Triangle at First Switch Point for Goods of Higher Order

Notice that the step for goods of first order is longer for the Beta technique. For goods of order 42 and higher, the step for the Alpha technique is higher. Since Beta is cost-minimizing at a lower interest rate around this interest rate, a lower interest rate is associated with the adoption of a shorter structure of production to produce more goods of the first order. This effect is perverse from the perspective of the Austrian story that Hayek developed his triangles to illustrate.

One can look at the ratio of successive increments of step sizes in these Hayekian triangles (Figure 5). This ratio is a constant for the Alpha technique. Because of the composition of the consumption good, this ratio does not vary with the order of goods. This ratio, for the Beta technique, approaches a constant as the order of goods increases without bound. Under the assumptions in which a Hayekian triangle can be constructed from a model of the production of commodities, this ratio always approaches a limiting value. This limit increases with the interest rate for which the triangle is constructed. It is smaller for a larger maximum interest rate. Since the intersection of the wage curves with the abscissa in Figure 1 is larger for Beta, the structure of production for Alpha is ultimately longer in Figure 4.

Figure 5: Ratios of Value Added at First Switch Point

5.0 Hayekian Triangles at the Second Switch Point

One can also consider Hayekian triangles at the second switch point (Figure 6). This switch point is perverse from the perspective of neoclassical theory. Around this switch point, the Alpha technique is cost-minimizing at a lower switch point. The Alpha technique has a longer structure of production and produces less goods of the first order. This pivoting of the structure of production is just the story that Hayek invented his triangles to tell.

Figure 6: Hayekian Triangle at Second Switch Point

"While the controversy about public works was developing, Professor Robbins sent to Vienna for a member of the Austrian school to provide a counter attraction to Keynes. I very well remember Hayek's visit to Cambridge on his way to the London School. He expounded his theory and covered a black board with his triangles. The whole argument, as we could see later, consisted in confusing the current rate of investment with the total stock of capital goods, but we could not make it out at the time. The general tendency seemed to be to show that the slump was caused by [excessive] consumption. R. F. Kahn, who was at that time involved in explaining that the multiplier guaranteed that saving equals investment, asked in a puzzled tone, 'Is it your view that if I went out tomorrow and bought a new overcoat, that would increase unemployment?' 'Yes,' said Hayek, 'but,' pointing to his triangles on the board, 'it would take a very long mathematical argument to explain why.'" -- Joan Robinson. 1972. The second crisis of economic theory.

Conclusion

The above has analyzed a reswitching example, with two techniques, in a model of the production of commodities by means of commodities. The switch point that is normal, from a mainstream neoclassical perspective, has perverse Hayekian triangles. The switch point that is perverse from a mainstream perspective has Hayekian triangles consistent with the Austrian story about how an increased time preference rotates the triangle to lengthen the structure of production. If the wage curve for Beta were concave to the origin, on the other hand, the first, normal switch point would also be normal from an Austrian perspective, and the second switch point would be perverse from both a neoclassical and Austrian perspective. But what would happen if only one or three switch points existed? Hayekian triangles cannot both be made rigorous and sustain an Austrian story on capital theory.

On the other hand, this post has shown that Austrian economists are correct to claim to have some perspectives distinct from mainstream economists. A refutation of tradional neoclassical capital theory is not, by itself, sufficient to refute all varieties of Austrian capital theory. Furthermore, the analysis in this post has illustrated that, in a model of the production of commodities, the ratio of step sizes in Hayekian triangles approaches a constant (as in Fillieule 2007), dependent on the interest rate for which the triangles are drawn and the maximum interest rate.

This post has drawn no conclusions about monetary theory or macroeconomics. Economists from the Austrian school often draw on capital theory for such purposes. Capital theory can hardly be radically modified without further consequences. Considering such consequences, however, has been on the agenda since Hayek (1941).

Adam Smith On A Labor Theory Of Value

The following are the first three paragraphs of the introduction to the Wealth of Nations:

"The annual labor of every nation is the fund which originally supplies it with all the necessaries and conveniencies of life which it annually consumes, and which consist always either in the immediate produce of that labour, or in what is purchased with that produce from other nations.

According, therefore, as this produce, or what is purchased with it, bears a greater or smaller proportion to the number of those who are to consume it, the nation will be better or worse supplied with all the necessaries and conveniencies for which it has occasion.

But this proportion must in every nation be regulated by two different circumstances: first, by the skill, dexterity, and judgment with which its labour is generally applied; and, secondly, by the proportion between the number of those who are employed in useful labour, and that of those who are not so employed. Whatever be the soil, climate, or extent of territory of any particular nation, the abundance or scantiness of its annual supply must, in that particular situation, depend upon those two circumstances." -- Adam Smith

When people talk about Adam Smith having a labor theory of value, they are not normally referencing the above. They are usually thinking of his few pages on a supposed "early and rude state of society which precedes both the accumulation of stock and the appropriation on land (book 1, chapter 6; see also book 1, chapter 8). Or they are thinking of his use of labor commanded as a measure of welfare (book 1, chapter 5).

But consider the above quotation. One can break down the annual labor of a nation in several ways. One can look at the proportion of the labor of the country which is needed to produce the necessaries for the entire labour employed. The remaining labour produces commodities that make up profits, interest, rent, payments to unproductive laborers, and so on.

This surplus can be consumed as necessaries and conveniences of life. One might call the latter luxuries. Or it might be used for accumulation. If the size of the labor force is to grow and the consumption of the individual worker is not to decrease, some of it must be used for accumulation. Smith thought that as the market increased, so would the division of labor. In a virtuous cycle, a greater proportion would be available for accumulation.

So in the very beginning of his most well-known book, Adam Smith points to the question of the size, distribution, and use of the surplus.

William Baumol On Marx

This is more for my commonplace book. The first two quotations are part of a symposium with Morishima and Samuelson:

"This paper will suggest that the meaning of the relationship between values and prices described in Capital has been widely misunderstood. Commentators as eminent as Mrs. Robinson and Professor Samuelson have sought in the transformation discussion issues which Karl Marx never meant it to contain. Writers on 'the transformation problem' since L. Bortkiewicz have focussed on an issue that is largely peripheral; and others like E. B6hm-Bawerk have asserted that there is a contradiction between the analyses of Volumes I and III which is certainly not to be found there unless lne reads into them an interpretation different from that which Marx repeatedly emphasized.

Interpretation of the intentions of the writings of the dead is always a questionable undertaking, particularly since defunct authors cannot defend themselves. Yet there are some cases in which a careful rereading of the pertinent writings indicates that the author did speak for himself and spoke very clearly-the trouble in such cases seems to be that somethinv aboit the onriinal nresentation prevents most readers, even some very careful ones, from seeing what the writer intended.

A notable case in point is D. Ricardo's discussion of the labor theory of value. It is hard to understand how a careful reader of any edition of the Principles can overlook Ricardo's recognition of the role of the quantity and the durability of capital in the determination of price. The labor theory is explicitly proposed as a remarkably good approximation to the determination of competitive price. But, ultimately, Ricardo holds to a cost of production theory of pricing, not to a pure labor theory. Yet until Stigler's fine article on the subject (1958), in which this is documented beyond any shadow of a doubt, virtually any text was prepared to ascribe to Ricardo the purest of labor theories, and even J. H. Hollander and E. Cannan (see G. J. Stigler for references) suggested that Ricardo retreated grudgingly under fire to the cost of production model of the third edition. Only a few commentators, notably A. Marshall, J. Viner, and P. Sraffa, saw Ricardo's analysis for what it so plainly was from the first edition on.

I emphasize this case for two reasons; first, because I will try to show that the correct interpretation of Marx' intentions is equally evident, and second, because I will suggest that the false analogy between Ricardo's and Marx' value theories may help to explain our misunderstanding of the latter...

...In Ricardo, the labor theory of value was meant as a good approximation to a full explanation of the determination of prices. However Marx probably never intended to produce such an approximation and it certainly was not his intention when he wrote about the transformation problem; yet that objective, or something close to it, is often attributed to Marx.

I will provide evidence that Marx did not intend his transformation analysis to show how prices can be deduced from values. Marx was well aware that market prices do not have to be deduced from values (nor, for that matter, values from prices). Rather, the two sets of magnitudes which are derived more or less independently were recognized by Marx to differ in a substantial and a systematic manner. A subsidiary purpose of the transformation calculation was to determine the nature of these deviations. But this objective and, indeed, any explanation of pricing as an end in itself, was of very little consequence to Marx, for the primary transformation was not from values into prices but, as Marx and Engels repeatedly emphasize, from surplus values into the non-labor income categories that are recognized by 'vulgar economists,' i.e., profits, interest, and rent." -- William J. Baumol. 1974. The transformation of values: What Marx 'really' meant (an interpretation). Journal of Economic Literature 12(1): 51-62.

"2. I am surprised that 'On the question of whether [Marx's] purpose was successful in some sense or another [Samuelson] can find only a few relevant paragraphs in Baumol's text.' I am surprised because, so far as I know, there is no such paragraph. The only objective of my paper was to determine what Marx had set out to accomplish and how Marx believed he had accomplished his objectives, because I don't think it is appropriate to criticize anyone until we are sure we are criticizing what he actually said, not what we suspect he might have said, or should have said, or someone else says he might have said...

...4. Professor Samuelson proposes his peace terms, which require me to admit that for an explanation of 'actual wage-profits distribution,' presumably as for an explanation of actual pricing of commodities, 'the Volume I analysis is indeed a detour.' So much I admit readily and without reservations, and I contend Marx would readily have admitted it too, for in fact he did so repeatedly. Actual prices and actual wages, profits, rents and interest payments clearly were to him explainable by the classical mechanism, which is what he admittedly took over in Volume III. Marx never claimed, in fact he specifically denied, that one gets better numbers for any of these magnitudes from a Volume I than from a Volume III analysis.

Thus, for his part, all that Professor Samuelson has to do to end the disagreement between us is to admit that Marx himself was not particularly interested in the determination of these magnitudes, which he considered a surface manifestation and were important to him only because he believed them to conceal the underlying social production relationships...

...One final comment. Obviously, Ricardo is not easy reading, and our predecessors did often hold a multiplicity of views among which they themselves were not always able to distinguish, and such problems are brushed aside far too often in writings But there are some cases, albeit rare, where an author has said clearly and repeatedly, 'I do mean A, I do not mean B,' yet many people have refused to listen. Ricardo did repeatedly say that his was a cost of production model. He did say, at length, in every edition of the Principles that quantity and durability of capital make a difference to value. I suggest to any interested reader that he treat himself to a reexamination of pages 3043 (from the third edition) and 52-66 (from the first edition) of Volume I of Piero Sraffa [5, 1951] to see whether he can come away disagreeing with Jacob Viner's (humorous?) conclusion that 'Ricardo's actual words show that from the first he held that the relative values of commodities are always partly dependent on the relative amounts of fixed capital employed in their production' (Viner's italics) [6, 1930]." -- William J. Baumol. 1974. The fundamental Marxian theorem: A reply to Samuelson: Comment. Journal of Economic Literature 12(1): 74-75.

Baumol returned to Marx in 1983:

"I find few things as discouraging as the persistent attribution of positions to a writer whose works contain repeated, categorical, indeed emotional, denuciations of those views. Marx's views on wages are a prime example. Both vulgar Marxists and vulgar opponents of Marx have propounded two associated myths: that he believed wages under capitalism are inevitably driven near some physical subsistence level, and that he considered this to constitute of robbery of the workers and a major evil of capitalism. Yet Marx and Engels tell us aggain and again, sometimes in the most intemperate language, that these views are the very opposite of theirs. These observations, incidentally, are hardly new discoveries..." -- William J. Baumol. (1983). Marx and the iron law of wages. American Economic Review 73(2): 303-308

The Production Of Commodities And The Structure Of Production

Many of my examples illustrate simple structures of production for models in which commodities are produced with commodities. Economists following the Austrian school often illustrate the structure of production with Hayekian triangles. Accordingly, this post illustrates a Hayekian triangle with a model in which commodities are produced out of commodities. I consider the case in which only circulating capital exists. This post is a rewrite of this one.

The following are taken as given for the technique in use:

• A: The nxn Leontief input-output matrix in physical terms. Assume all commodities are basic and the economy is productive.
• a₀: The n-element row vector of direct labor coefficients.
• d: An n-element column vector that is in the proportions in which commodities are consumed.

Define:

denom = a₀(I - A)^-1d

From the given data, one can find the quantities of labor-time in the first column below.

Distribution of Work in a Given Year

Labor Time	Purpose
a0d/denom	To produce (1/denom) d, a basket of commodities for consumption at the end of the current year.
a0A d/denom	To produce capital goods to be used to produce the (1/denom) d basket of commodities for consumption at the end of the next year.
a0A2 d/denom	To produce capital goods to be used to produce capital goods to produce the (1/denom) d basket of commodities for consumption at the end of two years hence.
...	...

The first column can be summed:

(1/denom) a₀(I + A + A² + ...)d = a₀(I - A)^-1d/denom = 1 person-year

So the above table shows a decomposition, per person-year, of employment in a given year. It is a Hayekian triangle. Because it is constructed from a model of the production of commodities, the elements go on forever. No last year exists in the future for which capital goods are currently being produced.

The capital goods, Aⁿ d, approach the ratios of Sraffa's standard commodity. Consequently, the ratio of labor inputs approaches a constant, related to the maximum rate of profits.

Hayekian triangles are not necessarily set out with a single physical measure of an unproduced input at each stage. The value of capital goods per worker varies because of three effects:

• Composition effect: a different mixture of capital goods is used for different rates of growth.
• Price Wicksell effect: the capital goods are re-evaluated at different prices with a different interest rate.
• Real Wicksell effect: the capital goods vary with the technique, and the cost-minimizing technique varies with the interest rate.

The wage-rate of frontier is useful for visualizing these effects. They do not go away just because one represents the structure of production as a Hayekian triangle. The sort of regularities that Machaj (2017), for example, assumes with variations in the interest rate lack logical foundation.

I want to that the price of the commodities consumed at the end of the year is:

[w(r)/denom] [a₀d + a₀A d (1 + r) + a₀A² d (1 + r)² + ... ]

The terms in the above are useful in representing a Hayekian triangle in price terms.

A model of the production of commodities by means of commodities with general joint production cannot necessarily be represented to a series of inputs of dated labor inputs. I go back and forth on my intution in the case of pure fixed capital.

References

• Renaud Fillieule. 2007. A formal model in Hayekian macroeconomics: the proportional goods-in-process structure of production. Quarterly Journal of Austrian Economics 10: 193-208.
• Harris, Donald J. 1973. Capital, distribution and the aggregate production function. American Economic Review 63(1): 110 - 113.
• Machaj, Mateusz. 2017. Money, Interest, and the Structure of Production: Resolving Some Puzzles in the Theory of Capital. Lanham: Lexington Books.

Maynard Keynes Making Fun Of The Austrian School

This is for my commonplace book.

"It is true that some lengthy or roundabout processes are physically efficient. But so are some short processes. Lengthy processes are not physically efficient because they are long. Some, probably most, lengthy processes would be physically very inefficient, for there are such things as spoiling or wasting with time. With a given labour force there is a definite limit to the quantity of labour embodied in roundabout processes which can be used to advantage. Apart from other considerations, there must be a due proportion between the amount of labour employed in making machines and the amount which will be employed in using them. The ultimate quantity of value will not increase indefinitely, relatively to the quantity of labour employed, as the processes adopted become more and more roundabout, even if their physical efficiency is still increasing. Only if the desire to postpone consumption were strong enough to produce a situation in which full employment required a volume of investment so great as to involve a negative marginal efficiency of capital, would a process become advantageous merely because it was lengthy; in which event we should employ physically inefficient processes, provided they were sufficiently lengthy for the gain from postponement to outweigh their inefficiency. We should in fact have a situation in which short processes would have to be kept sufficiently scarce for their physical efficiency to outweigh the disadvantage of the early delivery of their product. A correct theory, therefore, must be reversible so as to be able to cover the cases of the marginal efficiency of capital corresponding either to a positive or to a negative rate of interest; and it is, I think, only the scarcity theory outlined above which is capable of this.

Moreover there are all sorts of reasons why various kinds of services and facilities are scarce and therefore expensive relatively to the quantity of labour involved. For example, smelly processes command a higher reward, because people will not undertake them otherwise. So do risky processes. But we do not devise a productivity theory of smelly or risky processes as such. In short, not all labour is accomplished in equally agreeable attendant circumstances; and conditions of equilibrium require that articles produced in less agreeable attendant circumstances (characterised by smelliness, risk or the lapse of time) must be kept sufficiently scarce to command a higher price. But if the lapse of time becomes an agreeable attendant circumstance, which is a quite possible case and already holds for many individuals, then, as I have said above, it is the short processes which must be kept sufficiently scarce." -- John Maynard Keynes, The General Theory of Employment, Interest and Money, Chapter 16.

Before this quotation, Keynes notes that when people save, they do not put in future orders for specific capital goods. Savers want general power over wealth. Keynes is correct about this. Nevertheless, I can see how some might say capital theory has something to do intertemporal coordination of plans. Yet the Austrian school is mistaken about how they associate greater capital with more lengthy investments, in some sense.

Francis Spufford On Commodity Fetishism As A Dance

I have expressed an appreciation before of the section in Capital on commodity fetishism. Perhaps this section stands up to a critique of Marx's theory of value.

"But Marx had drawn a nightmare picture of what happened to human life under capitalism, when everything was produced only in order to be exchanged; when true qualities and uses dropped away, and the human power of making and doing itself became only an object to be traded. Then the makers and the things made turned alike into commodities, and the motion of society turned into a kind of zombie dance, a grim cavorting whirl in which objects and people blurred together till the objects were half-alive and the people were half-dead. Stock-market prices acted back upon the world as if they were independent powers, requiring factories to be opened or closed, real human beings to work or rest, hurry or dawdle; and they, having given the transfusion that made the stock prices come alive, felt their flesh go cold and impersonal on them, mere mechanisms for chunking out the man-hours. Living money and dying humans, metal as tender as skin and skin as hard a metal, taking hands, and dancing round, and round, and round, with no way ever of stopping: the quickened and the deadened, whirling on. That was Marx's description, anyway. And what would be the alternative? A dance of another nature, Emil presumed. A dance to the music of use, where every step fulfilled some real need, did some tangible good, and no matter how fast the dancers spun, they moved easily, because they moved to a human measure, intelligible to all, chosen by all. Emil gave a hop and shuffle in the dust." -- Francis Spufford, Red Plenty, Graywolf Press, 2010: 66-67.

I may write a short review of this novel. If I do, I think I will not first review the seminar at Crooked Timber on it.

A Derivation Of Prices Of Production With Linear Programming

1.0 Introduction

This post illustrates a derivation of prices of production, based on certain properties of duality theory as applied to linear programming. I strive to be more concise and elementary than previous expositions. This exposition is based on John Roemer's Reproducible Solution (Analytical Foundations of Marxian Economic Theory, Cambridge University Press, 1981).

You will find no utility maximization or supply and demand functions below. I have no need for such hypotheses. Nevertheless, one can read this derivation as consistent with marginalism.

2.0 Technology and Endowments

Two commodities, iron and corn, are produced in this example. Managers of firms know a technology consisting of the processes defined in Table 1. Each column shows the inputs and outputs for a process operated at a unit level. All processes take a year to complete and provide their output at the end of the year. Each process exhibits constant returns to scale (CRS). For convenience, assume all coefficients of production defined in the table are positive. The inputs to production are totally used up by operating these processes.

Table 1: The Technology

INPUTS	Processes
	Iron Industry		Corn Industry
	a	b	c	d
Labor	a0,1(a)	a0,1(b)	a0,2(c)	a0,2(d)
Iron	a1,1(a)	a1,1(b)	a1,2(c)	a1,2(d)
Corn	a2,1(a)	a2,1(b)	a2,2(c)	a2,2(d)
OUTPUT	1 ton iron	1 ton iron	1 bushel corn	1 bushel corn

The endowments of iron and corn in the firm's inventory at the start of the year are also given parameters. Table 2 lists the remaining variables in this post. Presumably, the endowments are from production during the previous year. They are unlikely to be in the proportions needed to continue production. For example, if the managers of a firm decide to specialize in producing corn, they will have no endowments of iron.

Table 2: Parameters and Variables

Additional Parameters
ω1	Endowment of iron (in tons) for the firm.
ω2	Endowment of corn (in bushels) for the firm.
Parameters taken as given by managers of the firm
p	Price of iron (in bushels per ton).
w	The wage (in bushels per person-year).
Decision Variables
q1(a)	Quantity of iron (in tons) produced by the first process.
q1(b)	Quantity of iron (in tons) produced by the second process.
q2(c)	Quantity of corn (in bushels) produced by the third process.
q2(d)	Quantity of corn (in bushels) produced by the fourth process.
r	The rate of profits.

3.0 The Primal Linear Program

Managers of firms choose the quantities to produce with each process to maximize the increment z in value, subject to the constraint that they can buy the needed inputs at the start of the year out of the revenue obtained by selling their endowment. The objective function for the primal linear program is:

z = {p - [p a_1,1(a) + a_2,1(a) + w a_0,1(a)]} q₁(a)

+ {p - [p a_1,1(b) + a_2,1(b) + w a_0,1(b)]} q₁(b)

+ {1 - [p a_1,2(c) + a_2,2(c) + w a_0,2(c)]} q₂(c)

+ {1 - [p a_1,2(d) + a_2,2(d) + w a_0,2(d)]} q₂(d)

The quantities in the square brackets above are the costs of operating each process at a unit level. A bushel corn is taken as numeraire. The quantities in the squiggly brackets are the net revenues (also known as accounting profits) of operating each process at a unit level. Scaling these net revenues by the level of operation for each process results in the total accounting profit for the firm.

The constraints are:

[p a_1,1(a) + a_2,1(a)] q₁(a)

+ [p a_1,1(b) + a_2,1(b)] q₁(b)

+ [p a_1,2(c) + a_2,2(c)] q₂(c)

+ [p a_1,2(d) + a_2,2(d)] q₂(d) ≤ p ω₁ + ω₂

q₁(a) ≥ 0, q₁(b) ≥ 0, q₂(c) ≥ 0, q₂(d) ≥ 0

The statement of the constraints is based on the assumption that wages are paid at the end of the year, not advanced at the start.

4.0 The Dual Linear Program

The above linear program has a dual. In the dual, the rate of profits r is chosen to minimize the charge y on endowments:

y = (p ω₁ + ω₂) r

Such that:

[p a_1,1(a) + a_2,1(a)](1 + r) + w a_0,1(a) ≥ p

[p a_1,1(b) + a_2,1(b)](1 + r) + w a_0,1(b) ≥ p

[p a_1,2(c) + a_2,2(c)](1 + r) + w a_0,2(c) ≥ 1

[p a_1,2(d) + a_2,2(d)](1 + r) + w a_0,2(d) ≥ 1

r ≥ 0

Each constraint in the dual specifies that the revenues obtained from operating a process at the unit level do not exceed the costs, where costs include a charge for the going rate of profits. In other words, no super-normal profits can be obtained.

5.0 Some Observations About Duality

The value of the objective functions are equal in the solutions to the primal and dual LPs. In other words, the increment in value obtained by the decisions of the manager of a firm is charged to the value of the endowment.

Suppose the solution of the primal LP results in some process being operated at a positive level. Then the corresponding constraint in the dual LP is met with equality in its solution. Likewise, if a constraint in the dual is met with inequality, then that process will not be operated in the dual.

If the rate of profits in the solution to the dual is positive, then the constraint in the primal LP will be met with equality. That is, the whole value of the endowment will be used for further production.

6.0 Prices of Production

I introduce a final assumption. The solution to these LPs must be such that the economy can continue. In the context of this exposition, some firms must produce iron, and some must produce corn. Thus, one of the first two constraints in the dual LP must be met with equality. One of next two constraints must also be met with equality.

Consider the case when only one of the processes for producing iron is operated, and the same is true of the processes for producing corn. The dual LP yields a system of two equations in three variables: the price of iron, the wage, and the rate of profits. This system specifies prices of production.

This formulation solves for the choice of the technique, as well as prices of production. It can be generalized to allow for the production of many more commodities and many more processes for producing each commodity. A generalization can allow for heterogeneous labor. Another generalization allows for the production and use of fixed capital, that is, machines that last for many years. For a given wage, prices and the rate of profits drop out of the equations for prices of production for the chosen technique. These prices do not support the parables often told in introductory economics classes with supply and demand. For example, unemployment cannot necessarily be eliminated by lowering the wage and encouraging firms to thereby hire more labor.

7.0 Conclusion

The above illustrates some elements of a theory of value. This is neither a labor theory of value, nor Marx's theory of value. The theory is focused on production and has implications about how labor is allocated among industries, a central concern of Karl Marx.

Nancy Kress On Global Inequality And Poverty

I picked up the novel that the following quotation is from because I think I recall Kress participating in conversations on Usenet years ago. This novel ended up more a political argument than I expected. It is for Genetically Modified Organisms (GMOs), done right. We should rather strive for plants for food resistant to insects, not resistant to pesticides, for example. I assume that Kress agrees with her heroine.

"He had spent the two-week winter vacation from school, which somehow got extended to nearly another week, with Jake in Los Angeles...

He left an eleven-year old nerd, dress in Levi's, a tee that said CHESS PLAYERS HAVE GREAT MOVES, and a baseball cap. He returned looking like a thirty-two-year-old investment banker trying to be cool, dressed in a $300 Ferragamo zip-front polo, designer jeans, and sockless shoes that cost more than my weekly salary. He carried a state-of-the-art laptop that could probably have moved satellites in orbit. Jake had invested in an independent production company that had struck movie gold with two wildly popular films about aliens who battled Earth. Jake was rich.

'Wow, look at you,' I said, not approvingly.

Ian could always read me. 'You don't like it. Dad said you wouldn't. But just because some of the world isn't blessed doesn't mean that we shouldn't enjoy the facts that through our own efforts, we are.'

I stared at him. No way that was Ian talking, or even Jake. I asked, 'Who is she?'

'Who's who?' But he shifted from one foot to the other as we faced each other at the SeaTac arrival gate. Passengers streamed past.

'Your dad's new girlfriend. It's okay, Ian, he's an adult. So am I.'

He turned sulky. 'Sage Scott.'

I blinked. She was a huge international star with more beauty than talent. 'Well,' I said heartily, 'that's fine. But -'

'Mom,' Ian blurted out, 'don't hassle me because I like money, okay.'

'Money is useful,' I said, and hugged him again.

But it wasn't that easy. With almost-teenagers, it never is. There were times during the next week when I wanted to apologize to my lone-dead parents for my own teen years.

Ian was disdainful of his old school and wanted to transfer to one that had a good lacrosse team.

Ian was disdainful of his old clothes.

Ian refused to go with me to the soup kitchen where once a week for years now, we'd helped feed the homeless.

When Ian said, 'People can always feed themselves if they just try, just like the rest of the world could if it got its act together. All you have to do is grow food,' I'd had enough. Arguments weren't going to do it here. He needed immersion learning.

'Pack up your designed duds,' I said. 'We're taking a field trip.'

'Where?'

'Overseas.'

'I don't want to. Mom, I missed enough school already.'

'Like you really mind that. And we'll only be gone for a long weekend, so pack up.'

He was eleven, and eleven-year-olds don't have household veto. Not in my house. Ian went with me. Sulky, barricaded during the long flight behind laptop and earbuds and resentment, he went.

Chennai was a huge, prosperous commercial and cultural center in southern India. A tourist draw, it had the gorgeous Kapaleeswarar Templd, museums, parks, a British fort dating from the Raj, the Tamil film industry. That was not the Chennai I took Ian to.

I'd arranged for a guide who, along with an armed bodyguard, took us to outlying slums, to coastal villages flooded by the rising sea, to fields so ravaged by inland drought or coastal salt water that they could grow nothing. Ian saw ragged, starving children living in tin boxes, beggars whose bones stuck out sharp as chisels, a fight over food on an aid truck that left two people lying bloody in the road. Each night I brought him back to Chennai to eat rich food in expensive restaurants. I spent the money from my divorce freely, and I didn't have to say a word.

Sweating in the heat, Ian said, 'Sage was wrong. Those people - they can't grow enought food.'

'No. Each year, childhood deaths from malnutrition rise sharply, and it's only going to get worse. The need for food is projected to rise 70 percent over the next thirty years. And as to poverty - well, a handful of super-rich people have as much money as the whole bottom half of the world's population put together.'

'That can't be right.'

'It's not right.'

'I mean, that can't be correct.'

'It is.'

He said nothing more, staring at a child digging through a stinking garbage dump for something to eat. Back at the hotel, after a shower, I saw him checking statistics on his laptop. At dinner he stared at the exquisitely cooked food on his plate.

'Mom, what can we do?'

'Donate. Understand the situation. Care.'

He picked up his fork, put it down again, scowled. But not, this time at me. I thought I saw down beginning on his upper lip - could that be true? So soon?

'I can sell a lot of my stuff,' Ian said, 'and donate the money.'

'That's your choice, honey,' I said. 'But keep what you really need. The trick is to decide what that is.'" -- Nancy Kress, Sea Change, Tachyon Publications, 2020.