A Three-Technique Pattern Over The Wage Axis

Figure 1: Wage Frontier for a Fixed Capital Example

This post presents a perturbation of parameters in a 'one good' model of fixed capital. The coefficients of production differ from those in this reswitching example. But the model has the same structure.

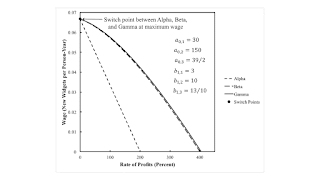
Consider a one-commodity economy in which labor and widgets are used to produce new widgets, the only consumption good. (The use of the term 'widget' to designate the single produced commodity emphasizes how unrealistic this model is.) New widgets last several years when used in producing widgets. In this particular answer to Steedman's homework assignment, they last three years. And their efficiency can vary throughout their technical lifetime. Accordingly, Tables 1 and 2 specify the coefficients of production for three processes.

Table 1: Inputs for The Technology

Input	Process
	(I)	(II)	(III)
Labor	a0,1	a0,2	a0,3
New Widgets	1	0	0
One-Year Old Widgets	0	1	0
Two-Year Old Widgets	0	0	1

Table 2: Outputs for The Technology

Output	Process
	(I)	(II)	(III)
New Widgets	b1,1	b1,2	b1,3
One-Year Old Widgets	1	0	0
Two-Year Old Widgets	0	1	0

Firms are not required to operate all three processes. They can truncate the use of widgets after one or two years. The choice of technique in this model is equivalent to the choice of the economic life of a widget. In the Alpha technique, the widget is operated for one year; in the Beta technique, it is operated for two years; and in the Gamma technique, it is operated for the full three years.

The wage frontier is the outer envelope of all wage curves. In models of circulating and fixed capital without superimposed joint production, the cost-minimizing technique, at a given rate of profits, is the technique which contributes its wage curve to the frontier at that rate. The Gamma technique is cost-minimizing in Figure 1 for all feasible rates of profits. Wage curves, when on the frontier, are declining functions of the rate of profits. At a switch point, more than one technique is cost-minimizing. At a rate of profits of zero in Figure 1, the Alpha, Beta, and Gamma techniques are all cost-minimizing.

The single switch point in Figure 1 is a fluke case several times over. It is the intersection of three wage curves, not two. And the switch point is on the wage axis, occurring for a rate of profits of zero. These properties are destroyed by any variation in certain coefficients of production. Figure 2 illustrates variations in b_1,2 and b_1,3. (The numbering of regions are consistent with this post.) The location in parameter space for fluke switch points, which I call patterns of switch points, is shown. Consider parameters in Region 4, and suppose b_1,2 is increased. Eventually, a fluke case will arise in which the switch point between the Alpha and Beta technique is on the wage axis. When b_1,2 > 10, this switch point will no longer occur for a non-negative rate of profits. It will only be cost-minimizing to run widgets for two or three years, depending on distribution. On the other hand, consider an increase in b_1,3. The switch points between Alpha and Beta and between Beta and Gamma will eventually coincide, in a single switch point at a positive rate of profits. With any further increase in this parameter, it is no longer cost minimizing to run widgets for two years, whatever the distribution of income.

Figure 2: Selected Regions in Parameter Space

Tables 3 and 4 summarize the choice of technique in each region in Figure 2. Negative real Wicksell effects occur at all switch points in the four regions in Figure 2. According to traditional Austrian and marginalist dogma, one might expect an increase in capital intensity to go along with a longer economic life of a widget. This idea is proven to be untrue in Regions 1, 4, and 5. Is the jump over an economic life of two years in Region 1 surprising? Adjacent techniques on the wage frontier need not be near in a parameter space formed by coefficients of production. Continuity in the wage frontier does not imply continuous variation in coefficients of production. In this case, the three-technique pattern of switch points illustrates how managers of firms come to eliminate the choice of the Beta technique.

Table 3: Variation in the Choice of Technique

1	0 ≤ r ≤ r1	Widgets operated for one year
	r1 ≤ r ≤ rγ	Widgets operated for three years
3	0 ≤ r ≤ rγ	Widgets operated for three years
4	0 ≤ r ≤ r1	Widgets operated for one year
	r1 ≤ r ≤ r2	Widgets operated for two years
	r2 ≤ r ≤ rγ	Widgets operated for three years
5	0 ≤ r ≤ r1	Widgets operated for two years
	r1 ≤ r ≤ rγ	Widgets operated for three years

Table 4: Summary of Local Structural Changes

1	A larger rate of profits is associated with a longer economic life of a widget.
3	No switch points.
4	A larger rate of profits is associated with a longer economic life of a widget.
5	A larger rate of profits is associated with a longer economic life of a widget.

This structure in a two-dimensional parameter space is generic, in some sense. Three partitions of patterns over the wage axis intersect in the start of a ray that is a partition for a three-technique pattern. A corresponding structure exists for patterns over the axis for the rate of profits.

The LTV And Commodity Fetishism

You will occasionally come upon supposed refutations of Marx's theory of value that I find just ignorant. One might talk about two divers. One comes up with a handful of sand, and the other comes up with a pearl. They have put in the same labor, but their products are of quite different exchange values. Or consider the labor that goes into making a useless product, something that cannot be sold as a commodity on a market. Obviously, labor does not create value.

A refutation can only be effective, at least among serious people, if it attempts to start with an understanding of the idea being attacked. A critique could be immanent and transcend the position it starts with. Or it can end up just rejecting that position.

I am not sure why I included a bit about commodity fetishism in my Frequently Asked Questions about the Labor Theory of Value. Apparently, one of my most popular posts is this one, in which I collect passages in Marx on vulgar political economy, commodity fetishism, and the illusions created by competition.

Marx, in Capital, for example, is analyzing the conditions that allow for a capitalist society to continue, to be self reproducing, albeit with fits and starts. One condition is that labor be distributed among many different concrete activities. For car and trucks to be produced, workers, besides making cars, maybe must be making tires out of rubber and steel out of iron, for example. And trucks or locomotives might be being driven to deliver steel or tires to outside of Detroit. The workers performing these activities are in a social relationship, but they do not see this. Even the managers of firms do not see this. Rather, this social relationship between workers is brought about by selling and buying commodities, such as tires, steel, and cars. Prices bopping about on markets bring about and maintain the relationships between workers. One can see why an analysis of capitalism might begin with an analysis of a commodity.

Individuals living in a self-reproducing society take on various roles, roles that cannot be defined in terms of a single individual or single transaction. Teachers cannot exist without students sometimes listening. And for a teacher to be a teacher, there cannot be just one teacher who once taught one student for one session. Instead, to be a teacher requires that one sometime has taught a student week after week. Nor can a king exist, Antoine de Saint-Exupery to the contrary, alone on an isolated asteroid. Subjects also must exist who acknowledge at least the possibility of sovereignty.

Marx treats the capitalist as 'capital personified'. The capitalist repeatedly uses money to buy raw materials and machinery (means of production) and hire workers (labor power). The workers make a commodity under the direction of the capitalist, and the capitalist owns what the worker makes. The capitalist must then sell the produced commodities on the market. The repeating of this process, time after time, is what makes a capitalist a capitalist according to Marx.

Neither capitalists nor workers calculate labor values. When the capitalist sells commodities on the market, he does not view the commodity as a 'material receptacle of homogeneous human labour'. And capitalists are not required to recognize that the relative prices of commodities express a social relationship characterizing how the total workforce is distributed among their establishments in the various industries in which production goes on in parallel.

Workers pressing for higher wages, less hours, and better working conditions also need no awareness of the labor time embodied in the commodities that they produce and in the commodities embodied in their wage. I take no issue, though, that it is helpful for workers and their advocates to have some awareness of the 'laws of motion' of the mode of production for the society in which they live.

It is a necessary consequence of this analysis that sometimes capitalists will direct workers to make something that cannot be sold as a commodity on the market. In some industries and processes, one expects a certain average failure rate. In oil drilling, for instance, one would expect a certain number of wells to fail. This rate may be lowered by technological advances, such as in controlled denotations and in signal processing applied to returns from various kinds of sensors. Likewise, if all of a company's research and development efforts pay off, it is not doing R and D right.

The deviation of market prices from prices of production is another reason sometimes some commodities cannot be sold on the market for prices that cover the average rate of profits. It is precisely the capitalists reactions to these deviations that bring about the social relationship between workers.

In this post, I have not even defined labor values, much less made any claims about quantitative relations between prices and labor values. I have also deliberately not used the phrase 'socially necessary abstract labor time' (SNALT). I think it clear that Marx thought that none of his claims depended on prices of production being proportional to labor values. I end where one could start with a mathematical treatment of Marx's theory of value. Only then could one argue about whether Sraffa's standard commodity does or does not provide a solution to the transformation problem.

References

• Arato, Andrew and Paul Breines. 1979. The Young Lukács and the Origins of Western Marxism. The Seabury Press.
• López, Daniel Andrés. 2019. Lukács: Praxis and the Absolute. Brill Books.
• Lukács, Georg. 1967. History and Class Consciousness. Trans. by Rodney Livingston.. Merlin.
• Rubin, Isaak I. Essays on Marx's Theory of Value.

Visualizing The Effects Of Parameter Perturbations In Models Of Joint Production

A Temporal Path

I have a new working paper.

Abstract: This article illustrates the analysis of prices of production with joint production by a numerical example. The example is used to illustrate the applicability of techniques to identify and visualize qualitative changes in the choice of technique with parameter perturbations. Patterns of switch points are knife-edge or fluke cases in which any perturbation of parameters results in such a qualitative change. This article identifies a new case, called a pattern for requirements for use, in which prices are indeterminate. If the proportions specified by requirements for use are varied at all, this indeterminancy vanishes.

I need more examples of flukes in models of pure joint production.

Elsewhere On 2020 'Nobel Prize'

• Edward Nik-Khan and Philip Mirowski in the New Statesman.
• National Public Radio's Planet Money.

I should have a link to somethingn written by Glen Weyl, not just hom being interviewed.

Fluke Switch Points At Both The Maximum Wage And The Maximum Rate Of Profits

Figure 1: Wage Frontier for a Fixed Capital Example

1.0 Introduction

I continue to explore the simplest multisector model of the production of commodities by means of commodities in which circulating and fixed capital is used in both sectors. In previous explorations, I locate a four-technique pattern, observe recurrence of truncation, and provide an example in which truncating all machines is infeasible.

I think my taxonomy of fluke switch points and methods of visualizing the effects of perturbing parameters, such as coefficients of production, applies unchanged to models of the production of commodities with fixed capital, maybe with certain simplifying assumptions. So I want to, at least, show fluke swith points of co-dimension one in models of fixed capital.

Every switch point is specified by the condition that two techniques be cost-minimizing at that switch point. The co-dimension is the number of additional conditions that must be met by that switch point:

• A pattern over the wage axis: The rate of profits is zero at the switch point.
• A pattern over the axis for the rate of profits: The wage is zero at the switch point.
• A three-technique pattern: A third technique is cost-minimizing at the switch point.
• A reswitching pattern: The two wage curves at the switch point.

So I am thinking of how to bring my examples of fixed capital together to show that all of these flukes are available with fixed capital. This post presents a global pattern which combines a pattern over the wage axis and a pattern over the axis for the rate of profits.

2.0 Technology

Table 1 specifies the coefficients of production for the example. In both the machine sector and the corn sector, an old machine cannot be transferred to the other sector. Corn is the consumption good and also acts as circulating capital. This is the simplest mutli-sectoral structure with both circulating and fixed capital in all sectors. The available techniques are defined in Table 2, unchanged from previous posts.

Table 1: Coefficients of Production for The Technology

Input	Process
	(I)	(II)	(III)	(IV)
Labor	1/10	8	43/40	1
Corn	0.548800712	1.7443584	0.125	0.282386
New Machines	1	0	1	0
Old Machines A	0	1	0	0
Old Machines B	0	0	0	1
Outputs
Corn	0	0	1	0.56
New Machines	2	5/2	0	0
Old Machines A	1	0	0	0
Old Machines B	0	0	1	0

Table 2: Techniques

Technique	Processes
Alpha	I, III
Beta	I, II, III
Gamma	I, III, IV
Delta	I, II, III, IV

3.0 Some Observations on Prices

The choice of technique can be analyzed by the construction of the wage frontier. Corn is the numeraire, and wages are assumed to be paid out of the surplus at the end of the year. As shown in Figure 1 above, the Gamma technique is cost-minimizing at any possible distribution of income. The economic life of a machine is truncated in the machine sector and operated for the full two years in the corn sector. At a rate of profits of zero, it is also cost-minimizing to truncate the machine in the corn sector. At a maximum rate of profits, it is also cost-minimizing to operate the machine for the full two years in the machine sector.

The analysis of the choice of technique is re-inforced by looking at prices. Figure 2 plots the price of a new machine as a function of the rate of profits, for all four techniques. At a switch point, the price of a new machine is the same for both techniques cost-minimizing at that rate of profits.

Figure 2: Price of New Machine

Figure 3 plots the price of an old machine in the machine sector. This price is zero for the Alpha and Gamma techniques, in which the economic life of the machine in the machine sector is truncated to one year. Up to the maximum rate of profits, the price of this type of old machine is negative for the Beta and Delta techniques. Thus, these techniques are not cost-minimizing. If either one of these techniques was in operation, managers of firms would be incentivized to truncate the operation of the machine after one year in the machine sector. At the switch point at the maximum rate of profits, the price of the old machine is zero. Thus, the machine could be operated for two years in the machine sector when the workers live on air.

Figure 3: Price of Old Machines in Machine Sector

Figure 4 shows the price of an old machine in the corn sector. Here the price of an old machine is zero for the Alpha and Beta techniques. The switch points are shown.

Figure 4: Price of Old Machines in Corn Sector

4.0 Perturbing Coeffients of Production for Circulating Capital Needed in Machine Sector

I now look at a slice of parameter space around the fluke case above. Consider small variations in a_1,1 and a_1,2, the bushels of corn need for input for a unit level of operation of the processes in the machine sector. At a unit level, these processes operate with a new machine and a one-year old machine, respectively, to produce new machines for use in either sector.

Figure 5 shows this slice of the parameter space around the fluke switch points in Figure 1. Variation in a_1,2 has no effect on the wage curves for the Alpha and Gamma techniques. Hence, the pattern over the wage axis is a vertical line in the figure. The pattern over the axis for the rate of profits is a diagonal line. The figure shows which techniques are cost-minimizing in which of the four 'quadrants' in which I have partitioned the parameter space.

Figure 5: Selected Regions in Parameter Space

Tables 3 and 4 summarize this local analysis. Around all switch points in illustrated regions of the parameter space, a lower rate of profits is associated with greater net output per person-year. In some sense, a lower rate of profits is associated, in this example, with the adoption of a more capital-intensive technique. But, for all switch points, examined here this increase in the amount of 'capital' used per worker is associated with a decrease in the economic life of a machine, in one sector or the other.

Table 3: Variation in the Choice of Technique

1	0 ≤ r ≤ r1	Operation of machine truncated in both sectors.
	r1 ≤ r ≤ r2	Operation of machine truncated after 1 year in machine sector. Operated for 2 years in corn sector.
	r1 ≤ r ≤ rδ	Machine operated for 2 years in both sectors.
2	0 ≤ r ≤ r1	Operation of machine truncated after 1 year in machine sector. Operated for 2 years in corn sector.
	r1 ≤ r ≤ rδ	Machine operated for 2 years in both sectors.
3	0 ≤ r ≤ r1	Operation of machine truncated in both sectors.
	r1 ≤ r ≤ rγ	Operation of machine truncated after 1 year in machine sector. Machine operated for 2 years in corn sector.
4	0 ≤ r ≤ rγ	Operation of machine truncated after 1 year in machine sector. Machine operated for 2 years in corn sector.

Table 4: Summary of Local Structural Changes

1	Larger rate of profits associated with longer economic life of machine in both sectors.
2	Larger rate of profits associated with longer economic life of machine in machine sector.
3	Larger rate of profits associated with longer economic life of machine in corn sector.
4	No switch points.

5.0 Conclusion

So that is another example of patterns around the wage axis and the axis for the rate of profits. I still have not found in this particular model examples of reswitching or capital-reversing. But I have such examples in other models of fixed capital. The above example, however, re-iterates that no connection exists between lengthening the economic life of a machine and an increase in the supply of 'capital'. Bohm-Bawerk was not incorrect merely because of the difficulty of defining a measure of the average period of production. His intuition, and not just his, on how prices work was itself incorrect.

Fields Impacted By The Cambridge Capital Controversy (CCC)

Some of these should have been more impacted:

• Macroeconomics: Measures of Total Factor Productivity, every model with an aggregate production function, and a belief that business cycles are to be explained by sticky or rigid prices or other imperfections are all shown to be questionable.
• Marxist economics: Steedman's Marx after Sraffa made a splash, with many writing afterwards. Lately, I've read a bit of Riccardo Bellofiore, but a bibliography here could go on and on.
• Monetary economics: Sraffa's work undermines the concept of the natural rate of interest and the concept of a neutral monetary policy. Colin Rogers' Money, interest and capital: A Study in the foundations of monetary theory goes into this.
• Labor economics: Here I point to my own stuff.
• Theory of the firm: Opocher and Steedman's Full Industry Equilibrium: A Theory of the Industrial Long Run is an adequate illustration.
• Industrial Organization: I have been working on a contribution here.
• The theory of international trade: Mainwaring, Metcalfe, Parrinello, and Steedman have early contributions in this area.
• Spatial or regional economics: I'll mention Sheppard and Barnes's textbook The Capitalist Space Economy: Geographical Analysis After Ricardo, Marx, and Sraffa and the work of Walter Isard with different regions being modeled by interacting Leontief matrices.
• Environmental or ecological economics: I think of Robin Hahnel's recent work on throughput or Richard England (1986) drawing connections between ecological costs and the functional distribution of income.

I do not claim that the above list is complete.

Infeasibility Of All Machines Truncated

Figure 1: Factor Wage Curves For Feasible Techniques

There are 12 coefficients that can be varied in my minimum multisector model in which production in all sectors can require both fixed and circulating capital. I do not think I am being very orderly in exploring this twelve-dimensional space.

This is a fluke case in which the maximum rate of profits is zero for both the Alpha and the Beta techniques. If only new machines are used as means of production in producing new machines and in producing corn, no surplus product is available to pay out as wages and profits. Likewise, if a machine is run for its full physical lifetime of two years in the machine sector, but truncated in the corn sector, no surplus product is, once again, available. But this is a feasible technology in that a surplus product is available when machines are operated for a full two years in the corn sector. (If a_{1, 1} and a_{1, 2} are slightly increased, the maximum rate of profits is negative for both the Alpha and Gamma techniques. Then this would be a non-fluke case.)

Managers of firms choose among feasible techniques by deciding whether or not to operate machines for two years, or to truncate their use, in the machine sector. As shown by the wage frontier above, their decision varies with the distribution of income. Baldone (1980) notes the possibility that for a viable technology with fixed capital, the truncation of the economic life of a machine may result in a non-viable technology. In an already long paper, he does not have a numerical example, however. By the way, Baldone has an appendix with a numerical example of the recurrence of truncation.

For completeness, Table 1 specifies the coefficients of production. I also define the techniques, which are unchanged from previous posts exploring this model. I would be impressed if somewhere in this twelve-dimensional space, almost all phenomena noted in the literature for models of fixed capital and new cases could be found. I have yet to locate cases of reswitching in this model. By definition, I will not be able to find a 'one-good' model with reswitching in this model (albeit what happens if the coefficients of production are the same in the two sectors, perhaps extended to have the machine last three years?).

Table 1: Coefficients of Production for The Technology

Input	Process
	(I)	(II)	(III)	(IV)
Labor	1/10	8	43/40	1
Corn	0.875	2.1875	0.125	0.282386
New Machines	1	0	1	0
Old Machines A	0	1	0	0
Old Machines B	0	0	0	1
Outputs
Corn	0	0	1	0.56
New Machines	2	5/2	0	0
Old Machines A	1	0	0	0
Old Machines B	0	0	1	0

Table 2: Techniques

Technique	Processes
Alpha	I, III
Beta	I, II, III
Gamma	I, III, IV
Delta	I, II, III, IV

References

• Salvatore Baldone (1980) Fixed capital in Sraffa's theoretical scheme. Trans. in Pasinetti (1980).
• Christian Bidard (2020) The wage-minimisation property. Working paper 2020-17.
• Luigi L. Pasinetti, ed. (1980) Essays on the Theory of Joint Production. New York: Columbia University Press.
• Bertram Schefold (1980) Fixed capital as a joint proudct and the analysis of accumulation with different forms of technical progress. Trans. in Pasinetti (1980).
• Paolo Varri (1980) Prices, rate of profit and life of machines in Sraffa's fixed capital model. Trans. in Pasinetti (1980).

Recurrence Of Truncation In A Perturbation Analysis

Figure 1: Variation of Choice Of Technique with a Coefficient of Production

This post continues the analysis of this example. The coefficients of production and the techniques are the same as in the linked post, except here I consider the results of varying a_{1, 2}, the amount of corn needed as circulating capital in operating Process II at unit level. Figure 1 above shows how the choice of technique varies with this parameter. This is a two-sector model, in which new machines and corn are produced in both sectors. Corn acts as circulating capital, as the sole consumption good, and as the numeraire. Machines act as fixed capital. Managers of firms have the ability to run machines for two years in both sectors, but old machines cannot be transferred between sectors.

Table 1: Variation in the Choice of Technique

1	0 ≤ r ≤ r1	Operation of machine truncated in both sectors.
	r1 ≤ r ≤ rβ	Machine operated for 2 years in machine sector. Truncated after 1 year in corn sector.
2	0 ≤ r ≤ r1	Operation of machine truncated in both sectors.
	r1 ≤ r ≤ r2	Operation of machine truncated after 1 year in machine sector. Machine operated for 2 years in corn sector.
	r2 ≤ r ≤ r3	Machine operated for two years in both sectors.
	r3 ≤ r ≤ rβ	Machine operated for 2 years in machine sector. Truncated after 1 year in corn sector.
3	0 ≤ r ≤ r1	Operation of machine truncated in both sectors.
	r1 ≤ r ≤ r2	Operation of machine truncated after 1 year in machine sector. Machine operated for 2 years in corn sector.
	r2 ≤ r ≤ rδ	Machine operated for two years in both sectors.
4	0 ≤ r ≤ r1	Operation of machine truncated in both sectors.
	r1 ≤ r ≤ rγ	Operation of machine truncated after 1 year in machine sector. Machine operated for 2 years in corn sector.

One can tell a tale with this example by reading Figure 1 from right to left. Initially, managers of firms do not find it profitable to run a machine for more than one year in the machine sector. At a high rate of profits (or a low wage), they want to run the machine for two years in the corn sector. Meanwhile, the engineers are figuring out how to use less circulating capital with old machines in the sector manufacturing new machines. Eventually, as at the start, firms run machines in both sectors for one year for low rates of profits. But which sector they want to run machines for two years in at high rates of profits is reversed; at the end they run machines for two years only in the machine sector at high rates of profits. The above figure and table show this change coming about.

Table 2: Summary of Results

1	Larger rate of profits associated with longer economic life of machine in machine sector
2	Larger rate of profits associated with longer economic life of machine in machine sector; Recurrence of truncation in corn sector
3	Larger rate of profits associated with longer economic life of machine in both sectors
4	Larger rate of profits associated with longer economic life of machine in corn sector

The example can be used to highlight the falsity of outdated, archaic intuition associated with neoclassical and Austrian-school price theory. One might think that a desire of individuals to save more would be associated with an increased supply of capital. And this would drive the interest rate down. A lower interest rate would supposedly induce firms to adopt more capital-intensive techniques and to run machinery longer. The adoption of more capital-intensive techniques would, in turn, lead to greater output per worker. Around each switch point in the example, a lower interest rate is indeed associated with the adoption of a technique which provides greater output per head. (This property does not generalize, as shown by examples of capital-reversing, also known as positive real Wicksell effects.) But, in the example, a lower interest rate is associated with the truncation of the economic life of machines, except in the corn sector in Region 2. In that region, a lower interest rate is first associated with an increase of the economic life of the machine and then, for an even lower interest rate, a truncation of its life in the corn sector. The economic life of the machine does not even bear a monotonic relationship with the interest rate.

Notice that I am not arguing about aggregate measures of capital or the so-called average period of production. An analysis of prices of production shows that out-dated neoclassical and Austrian-school economists just have a faulty understanding of microeconomics, of how prices work.

I guess this example is something different than the recurrence of a process, given the specific manner in which fixed capital is involved. If you have thoroughly absorbed post Sraffian price theory, the recurrence of truncation is, I guess, no surprise. My contribution is in visualizing this possibility.