A Derivation Of Sraffa's First Equations

1.0 Introduction

Piero Sraffa wrote down his 'first equations' in 1927, for an economy without a surplus. D3/12/5 starts with these equations for an economy with three produced commodities. I always thought that they did not make dimensional sense, but Garegnani (2005) argues otherwise. This post details Garegnani's argument, albeit with my own notation.

There are arguments about how and why Sraffa started on his research project I do not address here. The question is how did he relate what he was doing at this early date to Marx. In addition to Garegnani, DeVivo, Gehrke, Gilibert, Kurz, and Salvadori are worth reading here.

2.0 Givens

I assume an economy in a self-replacing state in which n + 1 commodities are produced.

• c_0,0 is the input of the first commodity used in producing the output of the first industry.
• (c_{., 0})^T = [c_1,0, c_2,0, ..., c_n,0] are the inputs of the remaining n commodities used in producing the output of first industry.
• c₀ = [c_0,1, c_0,2, ..., c_0,n] are the inputs of the first commodity used in producing the output of the remaining industries
• The element c_i,j, i, j = 1, 2, ..., n, of the matrix C is the input of the ith commodity used in producing the output of the jth industry.
• q₀ = is the quantity produced of the first commodity.
• (q)^T = [q₁, q₂, ..., c_n] are the outputs of the remaining n commodities used in producing the output of first industry.

All quantities are given in physical units. I abstract from fixed capital; all inputs are used up in the production of the outputs. Table 1 presents these parameters for the first example in the first chapter in Sraffa 1960.

Table 1: The Example from Sraffa (1960), Chapter 1

Input	Industry
	Iron	Wheat
Iron	c0, 0 = 8 tons iron	c0 = [12 tons iron]
Wheat	c., 0 = [120 quarters wheat]	C = [280 quarters wheat]
Output	q0 = 20 tons iron	q = [400 quarters wheat]

The following must hold for economy to be in a self-replacing state:

q_i = c_i,0 + c_i,1 + ... + c_i,n, i = 0, 2, ..., n

All quantities are non-negative. The economy must hang together in some sense. In Sraffa's terminology, all commodities are basic.

3.0 Coefficients of Production

I like to think of the coefficients scaled for unit output in each industry. Accordingly, define:

a_{0, 0} = c_{0, 0}/q₀

(a_{., 0})_i = (c_{., 0})_i/q_j, i = 1, 2, ..., n

(a₀)_j = (c₀)_j/q_j, j = 1, 2, ..., n

(A)_i,j = (C)_i,j/q_j, i, j = 1, 2, ..., n

4.0 All Quantities Measured in Unit Outputs of the First Industry

The given inputs can be thought of as produced in the previous year. The amount of, say, iron directly used as input in producing other commodities is (a₀ q). Table 2 indicates how much iron is needed as input in all previous years.

Table 2: Iron Inputs for Other Commodities

Year	Iron
0	a0 q
1	a0 A q
2	a0 (A)2q
...	...
n	a0 (A)nq
...	...

Even though my notation picks out the first commodity, there is nothing special about it. Suppose some commodity is selected. Let v₀ be the quantity of this commodity needed directly and indirectly to produce a unit of the first commodity. Let v be the quantities of this commodity needed directly and indirectly to produce each of the remaining commodities. v₀ and v must satisfy the following system of n + 1 linear equations:

v₀ a_{0, 0} + v a_{., 0} = v₀

v₀ a₀ + v A = v

For a non-trivial solution to exist, the determinant of the matrix in Table 3 must be zero, which it is in the case pf the Sraffa example.

Table 3: A Matrix

1 - a0, 0 = (3/5) tons	-a0 = [(-3/100) tons]
-a., 0 = [-6 quarters]	I - A = [(3/10) quarters]

I set v₀ to unity. The amount of this commodity used directly and indirectly in the production of all other commodities is easily found:

v = a₀(I - A)^-1

5.0 Rescaling the Givens

I then rescale the givens.

b_{0, 0} = v₀ c_{0, 0}

b_{i, 0} = v_i (c_{., 0})_i, i = 1, 2, ..., n

b_{0, j} = v₀ (c₀)_j, j = 1, 2, ..., n

b_{i, j} = v_i c_{i, j}, i, j = 1, 2, ..., n

s₀ = v₀ q₀

s_i = v_i q_i, i = 1, 2, ..., n

Table 4 presents Sraffa's example with these calculations. Here, a unit of wheat is 10 quarters. That is, one ton iron is used directly and indirectly in producing 10 quarters of wheat.

Table 4: Sraffa's Example Again

Input	Industry
	Iron	Wheat
Iron	b0, 0 = 8 tons iron	b0 = [12 tons iron]
Wheat	b., 0 = [12 tons wheat]	B = [28 tons wheat]
Output	s0 = 20 tons iron	s = [40 tons wheat]

I then have Sraffa's 'first equations':

b_{0, j} + b_{1, j} + ... + b_{n, j} = s_j, j = 0, 1, ..., n

For the economy to be in a self-replacing state, the following must hold:

b_{i, 0} + b_{i, 1} + ... + b_{i, n} = s_i, i = 0, 1, ..., n

Even though I am adding together, say, quantities of iron and wheat, the dimensions are consistent.

6.0 A Re-interpretation

Suppose the first produced commodity is labor, not iron. c_{0, 0} becomes the amount of labor performed in households (outside the market) to reproduce the labor force. c_{., 0} is the commodity basket paid out in wages when the workers obtain all of the surplus product. a₀ are the direct labor coefficients for each industry, and A is the Leontief input-output matrix. v is the vector of labor valus (also known as employment multipliers). Under the assumptions, prices of production are identical to labor values.

This model is descriptive. The givens do not show how required inputs might decrease with innovation or the formal and real subsumption of labor.

References

• Garegnani, Pierangelo (2005) On a turning point in Sraffa's theoretic and interpretative position in the late 1920s. European Journal of the History of Economic Thouht 12 (3): 453-492.
• Gehrke, Christian, Heinz D. Kurz, and Neri Salvadori (2019) On the 'origins' of Sraffa's production equations: A reply to de Vivo. Review of Ploitical Economy 31 (1): 100-114.

Towards the Derivation of the Cambridge Equation with Expanded Reproduction and Markup Pricing

I have a new working paper.

Abstract: Does the Cambridge equation, in which the rate of profits in a steady state is equal to the quotient of the rate of growth and the savings rate out of profits, hold in an economy with widespread non-competitive markets? This article presents a multiple-good model of markup pricing in an attempt to answer this question. A balance equation is derived. Given competitive conditions, this model can be used to derive the Cambridge equation. The Cambridge equation also holds in a special case of markup pricing, with one capital good and many consumption goods being produced. No definite conclusions are reached in the general case.

The Cambridge Equation, Expanded Reproduction, and Markup Pricing: An Example

1.0 Introduction

I have sometimes set out Marx's model of expanded reproduction, only with prices of production instead of labor values. I assume two goods, a capital good and a consumption good, are produced with constant technology. If one assumes workers spend all their wages and capitalists save a constant proportion of profits, one can derive the Cambridge equation in this model.

The Cambridge equation shows that, along a steady state growth path, the economy-wide rate of profits is determined by the ratio of the rate of growth and the saving rate out of profits. Maybe one should not use causal language here. The Cambridge equation is a necessary, consistency condition for smooth reproduction in a capitalist economy.

This post derives the Cambridge equation with markup pricing, in a highly aggregated model of expanded reproduction. I am curious how far this result generalizes. I am thinking of a model in which, say, n capital goods are produced in Department I and m consumer goods are produced in Department II. At this point, I am not thinking of generalizations in which workers save and therefore own some of the capital stock. Nor am I worrying about fixed capital, depreciation, and technical change.

Table 1: Definition of Variables

Variable	Definition
a01	The person-years of labor hired per unit output (e.g., ton steel) in the first sector.
a02	The person-years of labor hired per unit output (e.g., bushel corn) in the second sector.
a11	The capital goods (measured in tons) used up per unit output in the first (steel-producing) sector.
a12	The capital goods (measured in tons) used up per unit output in the second (corn-producing) sector.
p1	The price of a unit output in the first sector.
p2	The price of a unit output in the second sector.
s1	Relative markup in producing steel.
s2	Relative markup in producing corn.
r̂	The scale factor for the rate of profits.
r	The rate of profits.
σ	The savings rate out of profits.
w	The wage, that is, the price of hiring a person-year.
c	Consumption per worker, in units of bushels per person-year.
X1	The number of units (ton steel) produced in the first sector.
X2	The number of units produced (bushels corn) in the second sector.
g	The rate of growth.

2.0 The Model

Certain quantity equations follow from the assumptions. No produced capital goods remain each year after subtracting those used to reproduce the capital goods used up in throughout the economy and those needed to support the given rate of growth:

0 = X₁ - (1 + g)(a₁₁ X₁ + a₁₂ X₂)

Consumption per person year is the output of the second department:

c = X₂

The model economy is scaled such that one person-year is employed:

a₀₁ X₁ + a₀₂ X₂ = 1

I have the usual price equations, with labor advanced:

p₁ a₁₁ (1 + r̂ s₁) + a₀₁ w = p₁

p₁ a₁₂ (1 + r̂ s₂) + a₀₂ w = p₂

The consumption good is the numeraire:

p₂ = 1

As with Marx in volume 2 of Capital, industries are here grouped into two great departments (Table 1). Means of production (also known as capital goods) are produced in Department I, and means of consumption (or consumer goods) are produced in Department II.

Table 2: Value of Outputs by Department and Distribution

Department	Capital	Wages	Profits
I. Capital Goods	a11 X1 p1	a01 X1 w	a11 X1 p1 s2 r̂
II. Consumption Commodities	a12 X2 p1	a02 X2 w	a12 X2 p1 s2 r̂

The overall, economy-wide rate of profits is defined in terms of profits and capital advances, aggregated over both departments:

r = (a₁₁ X₁ p₁ s₂ r̂ + a₁₂ X₂ p₁ s₂ r̂)/(a₁₁ X₁ p₁ + a₁₂ X₂ p₁)

The economy experiences expanded reproduction when it consistently expands each year. In this case, the demand for capital goods from the second department includes the savings of the capitalists receiving profits from that department. Likewise, the demand for consumption goods from the first department excludes the savings of the capitalists in that department. Observing these qualifications, it is easy to mathematically express the condition that the demand for capital goods from the second department match the demand for consumption goods from the first department:

a₀₁ X₁ w + (1 - σ) a₁₁ X₁ p₁ s₂ r̂ = a₁₂ X₂ p₁ + σ a₁₂ X₂ p₁ s₂ r̂

3.0 Some Aspects of The Model Solution

Quantity variables (c, X₁, and X₂) can be found as a function of the rate of growth. Price variables (w, p₁, and p₂) can be found as a function of the scale factor for the rate of profits. These solutions allow one to use the balance equation to find a relation between the scale factor for the rate of profits:

r̂ = (g/σ){1/[s₂ - (1 - g)(s₂ - s₁)a₁₁]}

One can use the above relationship and the solution quantities and prices to find the economy-wide rate of profits:

r = g/σ

Along a path in which the economy steadily expands, the rate of profits must be equal to the quotient of rate of growth and the savings rate out of profits. The rate of profits is dependent on investment and savings decisions, out of the control of the workers. (In a two-class economy in which the workers save at a smaller rate than the capitalists, the Cambridge equation remains valid, with the savings rate in the denominator being that of the capitalists.) It is independent of the technical conditions of the chosen technique, and marginal productivity has nothing to do with it.

4.0 Conclusions

I know that this model can be generalized to hold when any number of consumer goods are produced. I have not yet been able to show the Cambridge equation holds when any number of capital goods are produced.

A Semi-Idyllic Golden Age

1.0 Introduction

This post presents a model of a steady state with a constant rate of growth in which:

• Total wages and total profits grow at the same rate.
• Neutral technical change increases the productivity of labor in all industries.
• The wage per hour increases with productivity.
• Each worker continues to consume the same quantity of produced commodities.
• But each worker takes advantage of increased productivity to work less hours per year.

In these times, when concerns about global warning are so important, one would also want to see a suggestion of a reduced ecological footprint. So this model of a steady state is only semi-idyllic.

I do not consider anything in the mathematical model below to be original. I outline it to raise the question whether such a growth path is possible under capitalism. The model demonstrates logical consistency, but cannot demonstrate that details abstracted from in the model would not prevent its realization.

2.0 The Model

Consider a closed economy with no foreign trade. Industries are grouped into two great departments. In Department I, firms produce means of production, also known as capital goods. The output of Department I is called ‘steel’ and measured in tons. In Department II, firms produce means of consumption, also known as consumer goods. The output of Department II is called ‘corn’, measured in bushels. Both steel and corn are produced from inputs of steel and labor.

Constant coefficients of production (Table 1) are assumed to characterize production in each year. All capital is circulating capital. Long-lived machines, natural resources, and joint production are abstracted from in this model. Free competition is assumed. Labor is advanced, and wages are paid out of the net output at the end of the year. Workers are assumed to spend all of their wages on means of consumption. Profits are saved at a constant proportion, s.

Table 1: Constant Coefficients of Production

Parameter	Definition	Units
a0, 1(t)	Labor required as input per ton steel produced in year t.	Person-Hrs per Ton
a1, 1	Steel services required as input per ton steel produced.	Tons per Ton
a0, 2(t)	Labor required as input per bushel corn produced in year t.	Person-Hrs per Bushel
a1, 2	Steel services required as input per bushel corn produced.	Tons per Bushel

Suppose coefficients of production for steel inputs are constant through time, but labor coefficients exhibit a growth in labor productivity of 100 ρ percent:

a_{0, j}(t + 1) = (1 - ρ) a_{0, j}(t), j = 1, 2

Let X_i(t), i = 1, 2; represent the physical output produced in each department in year t and available at the end of the year. Furthermore, suppose the price of steel, p, and the rate of profits, r, are constant. Let outputs from each of the two departments grow at a constant rate of 100 g percent:

X_i(t + 1) = (1 + g) X_i(t), i = 1, 2

Certain quantity equations follow from these assumptions. The quantity of capital goods added each year must equal the capital goods remaining after reproducing those used up in producing total output, in both departments:

g [a_1,1 X₁(t) + a_1,2 X₂(t)]

= X₁(t) - [a_1,1 X₁(t) + a_1,2 X₂(t)]

The person-years of labor employed relates to labor coefficients and gross outputs:

L(t) = a_{0, 1}(t) X₁(t) + a_{0, 2}(t) X₂(t)

Price equations are:

p a_{1, 1} (1 + r) + a_{0, 1} w(t) = p

p a_{1, 2} (1 + r) + a_{0, 2} w(t) = 1

These equations embody the use of a bushel corn as numerate. w(t) is the wage per person-hour, paid out at the end of the year out of the surplus.

These assumptions and parameters are enough to depict Table 2. The column labeled "Constant capital" shows the value of advanced capital goods, taking the output of Department II as the numeraire. The column labeled "Variable Capital" depicts the wages paid out of revenues available at the end of the year. The surplus is what remains for the capitalists.

Table 2: A Tableau Economique

	Constant Capital	Variable Capital	Surplus	Output
I	p a1,1 X1(t)	w(t) a0,1 X1(t)	p a1,1 X1(t) r	p X1(t)
II	p a1,2 X2(t)	w(t) a0,2 X2(t)	p a1,2 X2(t) r	X2(t)

Workers spend what they get, and capitalists save a constant ratio, s, of their profits. With these assumptions, one can calculate the bushels corn that the workers and capitalists in Department I want to purchase, at the end of each year, from Department II. Likewise, one can calculate the numeraire value of the steel that capitalists in Department II want to purchase from Department I. Along a steady state, these quantities must be in balance:

[a_{0, 1}(t) w(t) + (1 - s) p a_{1, 1} r] X₁(t)

= p a_{1, 2} [1 + s r] X₂(t)

This completes the specification of this model of expanded reproduction with technical change uniformly increasing the productivity of labor.

3.0 The Solution

Output per labor hour is found by solving the quantity equations:

X₁(t)/L(t) = a_{1, 2} (1 + g)/β(t, g)

X₂(t)/L(t) = [1 - a_{1, 1} (1 + g)]/β(t, g)

where:

β(t, g) = a_{0, 2}(t) + [a_{0, 1}(t) a_{1, 2} - a_{0, 2}(t) a_{1, 1}](1 + g)

That is:

X_i(t)/L(t) = [1/(1 - ρ)^t] [X_i(0)/L(0)], i = 1, 2

The path of employed labor hours falls out as:

L(t) = (1 - ρ)^t (1 + g)^t L(0)

The number of employed person-hours decreases if:

ρ > g

The above expresses the condition that the labor inputs needed to produce a unit of output, in both departments, decrease faster than the rate of growth in both departments.

The price equations are also easily solved. Given a constant rate of profits, the price of steel is constant as well:

p = a_{0, 1}(0)/β(0, r)

The wage per person-hour increases with productivity:

w(t) = [1 - a_{1, 1} (1 + r)/β(t, r) = [1/(1 - ρ)^t] w(0)

The trade-offs between consumption per worker and the steady-state rate of growth and between the wage and the rate of profits have the same form.

These solutions can be substituted into the balance equation. It becomes:

[1 - a_{1, 1} (1 + s r)] (1 + g) = [1 - a_{1, 1} (1 + s r)] (1 + s r)

Suppose the rate of profits falls below its maximum (where the workers ‘live on air’) or not all profits are saved. Then this is a derivation of the "Cambridge equation":

r = g/s

A steady rate of growth, when the workers consume their wage, requires that the rate of profits be the quotient of the rate of growth and the savings rate out of profits.

4.0 Demographics and Institutions

I make some rather arbitrary assumptions about demographics and institutions. Suppose the number of person-years supplied as labor grows at the postulated rate of growth:

L_S(t + 1) = (1 + g) L_S(t)

with L_S(t) measured in person-years. Let the number of hours in a standard labor-year, α(t) decrease at the same constant rate as the growth in productivity:

α(t + 1) = (1 - ρ) α(t)

The rate at which the total supply of labor-hours increases is easily calculated:

α(t + 1) L_S(t + 1) = (1 - ρ) (1 + g) α(t) L_S(t)

Under these assumptions, the supply of labor-hours grows at the same rate as the demand for labor-hours. Total wages and total profits increase at the same rate, 100 g percent. The wage per worker increases at the same rate as the standard length of a labor year declines. Thus, workers consume a constant quantity of commodities, but they take increased productivity in steadily increased free time.

5.0 Discussion and Conclusions

What should one postulate about money in this model? One could assume the money supply grows endogenously, along with commodities. Or, perhaps, the velocity of the circulation of money increases with productivity. A continuous decrease in the money price of corn is another logical possibility. Perhaps Rosa Luxemburg was right, and an external source of demand from less developed regions and countries is needed to support expanded reproduction. Or Kalecki is correct, and military spending by the government will do.

I do not know if this model describes any existing capitalist economy. It does not describe the post-war golden age. In that time, at least in the United States, workers took increased productivity in increased consumer goods. (I think the memory of the Great Depression, the occurrence of World War II, and the existence of the Soviet Union has something to do how this worked out.) Could any capitalist economy function like this? Somehow, an advertising industry is not encouraging workers to consume ever more produced commodities, or they ignore such messages. They continually have more freedom. Yet, they always spend a bit of time under the domination and direction of their employers. Will the capitalists tolerate this?

Bifurcations With Variations In The Rate Of Growth

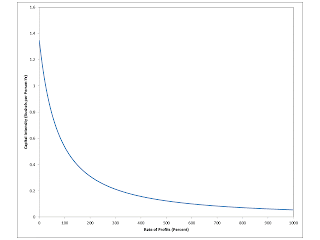
Figure 1: Perversity and Non-Perversity in the Labor Market Varying with the Rate of Growth

1.0 Introduction

I have been considering how the existence and properties of switch points vary with parameters specifying numerical examples of models of the production of commodities by means of commodities. Here are some examples of such analyses of structural stability. This post adds to this series.

I consider a change in sign of real Wicksell effects to be a bifurcation. In the model in this post, the steady state rate of growth is an exogenous parameter. So a change of sign of real Wicksell effects, associated with a variation in the steady state rate of growth, is a bifurcation.

2.0 Technology

The technology for this example is as usual. Suppose two commodities, iron and corn, are produced in the example economy. As shown in Table 1, two processes are known for producing iron, and one corn-producing process is known. Each column lists the inputs, in physical units, needed to produce one physical unit of the output for the industry for that column. All processes exhibit Constant Returns to Scale, and all processes require services of inputs over a year to produce output of a single commodity available at the end of the year. This is an example of a model of circulating capital. Nothing remains at the end of the year of the capital goods whose services are used by firms during the production processes.

Table 1: The Technology for a Two-Industry Model

Input	Iron Industry		Corn Industry
Labor	1	305/494	1
Iron	1/10	229/494	2
Corn	1/40	3/1976	2/5

For the economy to be self-reproducing, both iron and corn must be produced each year. Two techniques of production are available. The Alpha technique consists of the first iron-producing process and the sole corn-producing process. The Beta technique consists of the remaining iron-producing process and the corn-producing process.

Each technique is represented by a two-element row vector of labor coefficients and a 2x2 Leontief input-output matrix. For example, the vector of labor coefficients for the Beta technique, a_{0, β}, is:

a_{0, β} = [305/494, 1]

The components of the Leontief matrix for the Beta technique, A_β, are:

a_{1,1, β} = 229/494

a_{1,2, β} = 2

a_{2,1, β} = 3/1976

a_{2,2, β} = 2/5

The labor coefficients for the Alpha technique, a_{0, α}, differ in the first element from those for the Beta technique. The Leontief matrix for the Alpha technique, A_α, differs from the Leontief matrix for the Beta technique in the first column.

(The mathematics in this post is set out in terms of linear algebra. I needed to remind myself of how to work out quantity flows with a positive rate of growth. I solved the example with Octave, the open-source equivalent of Matlab for the example. I haven't checked the graphs by also working them out by hand. You can click on the figures to see them somewhat larger.)

3.0 Prices and the Choice of Technique

Consider steady-state prices that repeat, year after year, as long as firms adopt the same technique. Let a₀ and A be the labor coefficients and the Leontief matrix for that technique. Suppose labor is advanced and wages are paid out of the surplus at the end of the year. Then prices satisfy the following system of equations:

p A (1 + r) + a₀ w = p

where p is a two-element row vector of prices, w is the wage, and r is the rate of profits. Let e be a column vector specifying the commodities constituting the numeraire. Then:

p e = 1

For the numerical example, a bushel corn is the numeraire, and e is the second column of the identity matrix. I think of the numeraire as in the proportions in which households consume commodities.

The system of equations for prices of production, including the equation for the numeraire, has one degree of freedom. Formally, one can solve for prices and the wage as functions of an externally given rate of profits. The first equation above can be rewritten as:

a₀ w = p [I - (1 + r) A]

Multiply through, on the right, by the inverse of the matrix in square brackets:

a₀ [I - (1 + r) A]^-1 w = p

Multiply through, again on the right, by e:

a₀ [I - (1 + r) A]^-1 e w = p e = 1

Both sides of the above equation are scalars. The wage is:

w = 1/{a₀ [I - (1 + r) A]^-1 e}

The above equation is called the wage-rate of profits curve or, more shortly, the wage curve. Prices of production are:

p = a₀ [I - (1 + r) A]^-1/{a₀ [I - (1 + r) A]^-1 e}

The above two equations solve the price system, in some sense.

Figure 2 plots the wage curves for the example. The downward-sloping blue and red curves show that, for each technique, a lower steady-state real wage is associated with a higher rate of profits. The two curves intersect at the two switch points, at rates of profits of 20% and 80%. For rates of profits between the switch points, the Alpha technique is cost-minimizing and its wage curve constitutes the outer envelope of the wage curves in this region. For feasible rates of profits outside that region, the Beta technique is cost-minimizing. (I talk more about this figure at least twice below.)

Figure 2: Wage Curves also Characterize Tradeoff Between Consumption per Worker and Steady State Rate of Growth

4.0 Quantities

Suppose the steady-state rate of growth for this economy is 100 g percent. A system of equations, dual to the price equations, arises for quantity flows. Let q denote the column vector of gross quantities, per labor-year employed, produced in a given year. Let y be the column vector of net quantities, per labor-year. Net quantities constitute the surplus once the (circulating) capital goods advanced at the start of the year, for a given technique, are replaced:

y = q - A q = (I - A) q

Since quantities are defined per person-year, employment with these quantities is unity:

a₀ q = 1

By hypothesis, net quantities are the sum of consumption and capital goods to accumulate at the steady state rate of profits:

y = c e + g A q

Substituting into the first equation in this section and re-arranging terms yields:

c e = [I - (1 + g) A] q

Or:

c [I - (1 + g) A]^-1 e = q

Multiply through on the left by the row vector of labor coefficients:

c a₀ [I - (1 + g) A]^-1 e = a₀ q = 1

Consumption per person-year is:

c = 1/{a₀ [I - (1 + g) A]^-1 e}

Gross quantities are:

q = [I - (1 + g) A]^-1 e/{a₀ [I - (1 + g) A]^-1 e}

Interestingly enough, the relationship between consumption per worker and the rate of growth is identical to the relationship between the wage and the rate of profits. Thus, Figure 1 is also a graph of the trade-off, for the two technique, between steady-state consumption per worker and the rate of growth. One can think of the abscissa as relabeled the rate of growth and the ordinate as relabeled consumption per person-year. In the graph, the grey point illustrates consumption per worker at a rate of growth of 10% for the Beta technique.

The ordinate on this graph is consumption throughout the economy. If the rate of profits exceeds the rate of growth, both those obtaining income from wages and those obtaining income from profits will be consuming. When the rates of growth and profits are equal, all profits are accumulated.

5.0 Some Accounting Identities

The value of capital per worker is:

k = p A q

The value of net income per worker is:

y = p y = p (I - A) q

(I hope the distinction between the scalar y and the vector y is clear in this notation.)

The value of net income per worker can be expressed in terms of the sum of income categories. Rewrite the first equation in Section 3:

p (I - A) = a₀ w + p A r

Multiply both sides by the vector of gross outputs:

p (I - A) q = a₀ q w + p A q r

Or:

y = w + k r

In this model, net income per worker is the sum of wages and profits per worker.

Net income per worker can also be decomposed by how it is spent. For the third equation in Section 4, multiply both sides by the price vector:

p y = c p e + g p A q

Or:

y = c + g k

Net income per worker is the sum of consumption per worker and investment per worker.

Equating the two expressions for net income per worker allows one to derive an interesting graphical feature of Figure 1. This equation is:

w + r k = c + g k

Or:

(r - g) k = c - w

Or solving for the value of capital per worker:

k = (c - w)/(r - g)

Capital per worker, for a given technique, is the additive inverse of the slope of two points on the wage curve for that technique. Figure 1 illustrates for the Beta technique, with a rate of growth of 10% and a rate of profits of 80%, as at the upper switch point.

6.0 Real Wicksell Effects

This section and the next presents an analysis confined to prices at the switch point for a rate of profits of 80%.

For a rate of profits infinitesimally lower than 80%, the Alpha technique is cost-minimizing. And for a rate of profits infinitesimally higher, the Beta technique is cost minimizing. I have explained above how to calculate the value of capital per worker, for the two techniques, at any given rate of growth.

Abstract from any change in prices of production associated with a change in the rate of profits. The difference between capital per head for the Beta technique and capital per head for the Alpha technique, both calculated at the prices for the switch point, is the change in "real" capital around the switch point associated with an increase in the rate of profits. Figure 3 graphs this real Wicksell effect as a function of the rate of steady state growth.

Figure 3: Variation in Real Wicksell Effect with Steady State Rate of Growth

Two regions are apparent in Figure 3. The intersection, at the left, of the downward-sloping graph with the axis for the change in the value of capital per worker shows that the real Wicksell effect is positive, for this switch point, in a stationary state. Around the given switch point, a higher rate of profits is associated, in a stationary state, with firms wanting to adopt a more capital-intensive technique. If a greater scarcity of capital caused the rate of profits to rise, so as to ration the supply of capital, such a logical possibility could not be demonstrated.

The real Wicksell effect, for the switch point at the higher rate of profits, is zero when the rate of growth is equal to the rate of profits at the other switch points. The value of capital per person-year is the same for the two techniques, in this case. Consider a line, in Figure 1, connecting the two switch points. It also connects the points on the wage curve for the Alpha technique for a rate of profits of 80% and a rate of growth of 20%. And the same goes for the wage curve for the Beta technique.

7.0 Real Wicksell Effects in the Labor Market

A variation in real Wicksell effects with the steady state rate of growth is also manifested in the labor market. I have echoed above some mathematics which shows that the value of national income is the dot product of a vector of prices with the vector of net quantity flows. The price vector depends, given the technique, on the rate of profits at which prices of production are found. The quantity vector depends on the steady state rate of growth. The reciprocal, (1/y), is the amount of labor firms want to hire, per numeraire unit of national income, for a given technique. The difference at a switch point between these reciprocals, for the two techniques, is another way of looking at real Wicksell effects.

Around the switch point at a rate of profits of 80%, a lower wage is associated with firms adopting the Beta technique. And a higher wage is associated with firms adopting the Alpha technique. The difference of the above reciprocals, between the Alpha and Beta techniques, is the increase in labor, per numeraire-unit net output, associated with an infinitesimal increase in wages, at the prices for the switch point. Figure 1 shows this difference, as a function of the steady state rate of growth, at the switch point with the higher rate of profits in the example.

Figure 1 qualitatively resembles Figure 3. For a stationary state, a higher wage is associated with firms wanting to employ more labor, per numeraire unit of net output. This effect is reversed for a high enough steady state rate of growth. The bifurcation, here too, occurs at the rate of growth for the switch point at 20%.

8.0 Conclusion

This post has illustrated a comparison among steady state growth paths at rates of profits associated with a switch point. And this switch point is "perverse" from the perspective of outdated neoclassical theory, at least at a low rate of growth. But the perversity of this switch point varies with the rate of growth. In the example, when the rate of growth is between the rate of profits at the two switch points, the second switch point becomes non-perverse.

And it can go the other way. Real Wicksell effects do not even need to be monotonic. I need to find an example with at least three commodities, two techniques, and three switch points. In such an example, the switch point with the largest rate of profits will have a negative real Wicksell effect for a stationary state, a positive real Wicksell effect for steady state rates of growth between the first two switch points, and a negative real Wicksell effect for higher rates of growth, between the second and third switch points.

(I want to look up Gandolfo (2008) in the light of past posts. Can I tell this tale in terms of increasing returns, instead of exogenous technical change?)

References

• Giancarlo Gandolfo (2008). Comment on "C.E.S. production functions in the light of the Cambridge critique". Journal of Macroeconomics, V. 30, No. 2 (June): pp. 798-800.
• Nell (1970). A note on Cambridge controversies in capital theory. Journal of Economic Literature V. 8, No. 1 (March): 41-44.

On r > g

I have not even started to read Thomas Piketty's Capital in the Twenty-First Century, but I have heard of Piketty as compared to Marx.

Whatever else Marx was, he was a very learned man. He read the works of virtually all political economists who came before him. And in his lengthy tomes, he would comment on them, not always fairly. He did not confine himself to ones that were politically influential among the elite. For example, consider Marx on the Ricardian socialists.

So if Piketty is like Marx, can I expect to find comments on the Cambridge equation, r = g/s_c? Can I expect to find something about the models of growth and distribution put forward by Richard Kahn, Nicholas Kaldor, Luigi Pasinetti, and Joan Robinson? (Joshua Gans has also noticed a parallelism between the work of Piketty and the Post Keynesian theory of distribution.) Or maybe the analogy is not complete.

Rate of Profits And Value Of Stock Independent Of Workers Saving

.

1.0 Introduction

This post presents elements of a model of a smoothly reproducing economy, that is, of an economy growing along at the warranted growth rate. I have previously presented a more detailed exposition of a variant of this model. One could add, say, Harrod-neutral technical change to that exposition. I would find it easier to add biased technical change by assuming fixed, not variable, coefficients of production. Perhaps this model reflects conventions and the balance of class forces prevalent in Anglo-American economies after World War II and before the collapse of the Bretton Woods system.

Anyways, I am revisiting this model because, recently, I have noticed another mathematical property of this model. Not only are the determinants of the rate of profits along a warranted growth path independent of the decisions of the workers to save. So is the average stock price of corporations.

2.0 The Model

This model abstracts from the existence of government spending and taxation. It also treats foreign trade as negligible. National income is comprised of wages, W, and profits, P. The rate of profits, r, is the ratio of profits to the value of capital goods, K, used in producing national income.

2.1 The Corporate Sector

I begin with corporations. The corporations own the capital goods and hire the workers to produce output with these capital goods. Corporate managers decided on the level of investment, I, to achieve a target growth rate, g.

Investment, in this model, is financed by some mixture of retained profits and the issuance of new stock (also known as shares) on the stock market. Corporate managers decide on this mix. Let s_c be the proportion of profits that are retained to finance new investment. And let f be the proportion of investment financed by issuing new shares:

I = s_c P + f I

Some algebra yields:

P/K = [(1 - f)/s_c] (I/K)

Or:

r = [(1 - f)/s_c] g

Thus, the rate of profits consistent with a warranted rate of growth is determined by parameters characterizing decisions made by corporate managers.

2.2 Finances and Households

In this model, households do not own capital goods. Rather, corporations own capital goods, and households own stock in these corporations. The ratio of the market value of stock to the value of the capital goods owned by the corporations is called the valuation ratio, v. The valuation ratio is assumed constant along a warranted growth path. Variations in the valuation ratio reflect short-term speculation. Generally, the valuation ratio is above unity.

Households are divided into two classes in this model, workers and capitalists. Workers receive part of their income in the form of wages. Given a positive savings rate on the part of workers, they also receive dividends and capital gains from their stock. Capitalists do not labor; their households receive all their income from dividends and capital gains. The variable j is used to denote the proportion of stocks owned by the workers.

Dividends consist of profits received and not retained by the corporations. By assumption, the value of dividends is then (1 - s_c)P. Net investment, I, is the increase in the value over a year of the capital goods owned by corporations, while the increase in the value of stocks is vI. But the value of new shares is only fI. The difference, (v - f)I, is the value of capital gains.

The interest rate is the ratio of the returns to financial capital (that is, dividends and capital gains) to the value of stock. With a valuation ratio above unity the interest rate, i, falls below the rate of profits. The valuation ratio then becomes:

v = (r - g)/(i - g)

I assume workers typically save at the rate s_w, and capitalists typically save at the greater rate s_r. Table 1 shows sources of savings, based on these definitions and behavioral assumptions.

Table 1: Sources of Economy-Wide Savings

Source	Amount
Retained Earnings:	sc P
Capitalist Savings Out of Dividends:	(1 - j)sr(1 - sc)P
Minus Capitalist Consumption Out of Capital Gains:	- (1 - j)(1 - sr)(v - f)I
Worker Savings Out of Wages:	swW
Worker Savings Out of Dividends	j sw(1 - sc)P
Minus Worker Consumption Out of Capital Gains:	- j(1 - sw)(v - f)I

In adding up savings, one must be sure not to double-count retained earnings. Corporations decide to save retained earnings, but households can undo this decision by consuming capital gains. Total savings for capitalists, S_r, are:

S_r = (1 - j) s_r[(1 - s_c)P + (v - f)I]

Total savings for workers, S_w, are:

S_w = s_wW + j s_w[(1 - s_c)P + (v - f)I]

Along a warranted growth path, investment is always equal to savings. The following equation is based on the components in Table 1:

I = s_c P + (1 - j)[s_r(1 - s_c)P - (1 - s_r)(v - f)I]

+ s_wW + j [s_w(1 - s_c)P - (1 - s_w)(v - f)I]

A bit of algebra allows the investment-savings equality to be restated:

I = s_c P + S_r + S_w - (v - f)I

The last term (that is, capital gains) is subtracted to avoid double-counting.

Another condition of a warranted growth path in this model is that the corporate sector, capitalist households, and workers continue to endure. This condition requires that the rate of growth of the book-value of the capital goods held by the corporations, the rate of growth of the value of the stock held by capitalists, and the rate of growth of the value of the stock held by the workers all be equal. Thus, the rate of growth of the value of the stock held by capitalists is:

g = S_r/[(1 - j)v K]

The rate of growth of the value of the stock held by workers is:

g = S_w/(j v K)

This completes the exposition of the equations I need for my point here.

2.3 Some Algebra

I now report on some algebraic manipulations of these equations. The condition that the value of the stock held by capitalists and workers grows at the same rate yields the following condition:

S_w = S_r [j/(1 - j)]

Substituting in the investment-savings equality, one can obtain:

I = s_c P + [S_r/(1 - j)] - (v - f)I

Or, by expanding the definition of capitalist savings:

I = s_c P + s_r[(1 - s_c)P + (v - f)I] - (v - f)I

Regrouping yields:

[1 + (1 - s_r)(v - f)]I = [s_c + s_r(1 - s_c)]P

Dividing through by the book value of the capital goods owned by the corporations, one obtains:

r = {[1 + (1 - s_r)(v - f)]/[s_c + s_r(1 - s_c)]} g

Equating for the value of the rate of profits previously found, one obtains an expression for the valuation ratio in terms of model parameters:

v = {[s_r(1 - s_c)]/[s_c(1 - s_r)]} - {s_r/[s_c(1 - s_r)]} f

Notice the parameters on the right-hand-side characterize either corporate decisions or the decisions of capitalist households. The saving propensities of the workers do not enter into it. The more that corporations finance investment by issuing shares, instead of using retained earnings, the lower the valuation ratio is along a warranted growth path. If the proportion of profits distributed in dividends lies below the proportion of investment financed by issuing new stock, a smaller capitalist savings propensity is associated with a higher valuation ratio. In some sense, capitalists get what they spend.

3.0 Conclusions

This post has outlined some necessary properties of a warranted growth path in a model containing:

• Corporations, a capitalist class, and a class of workers.
• A stock market, in which ownership shares in the corporations are bought and sold.
• A growth rate determined by decisions of the corporate managers.

In this model, the decisions of the corporate manager as to the growth rate, retained earnings, and finance obtained by issues of new stock determine the rate of profits consistent with a warranted growth path. These decisions of the corporate managers, along with the savings propensities of the capitalists, determine the ratio of the price of stock to the book value of the capital goods owned by the corporations. A fortiori, these decisions also determine the interest rate. Within the limits where a warranted growth path exists, the savings propensities of the workers have no effect on the growth rate, the rate of profits, the price of stock, the interest rate, or the functional distribution of income. The savings decisions of the workers do affect, however, the personal distribution of income and the proportion of stock owned by the workers.

Appendix: Variable Definitions

• K is the book value of the capital goods, in numeraire units, owned by the corporations.
• I is investment, in numeraire units.
• P is corporate profits, in numeraire units.
• S_r is capitalist savings, in numeraire units.
• S_w is worker savings, in numeraire units.
• f is the proportion of investment financed by issuing new stock (also known as shares).
• g is the warranted rate of growth.
• i is the interest rate.
• j is the proportion of stock owned by workers.
• r is the rate of profits earned by the corporations on the book value of their capital stock.
• s_c is the proportion of profits retained by corporations.
• s_r is the (average and marginal) to save of the capitalists.
• s_w is the (average and marginal) to save of the workers.
• v is the valuation ratio, that is, the ratio of the value of the stocks of the corporations to their book value.

Reference

• Scott J. Moss (Dec. 1978). The Post-Keynesian Theory of Income Distribution in the Corporate Economy, Australian Economic Papers, V. 17, N. 31: pp. 302-322.

A Near-Term Goal

I would like to develop a numeric example with:

• Smooth production functions, and
• Properties analogous to the ones highlighted in this example.

One of the parameters of the utility functions in this example expresses the willingness of consumers to defer consumption. A greater willingness to defer consumption supposedly represents a greater supply of "capital", in some sense. In a "perverse" case, this greater supply, all else the same, is associated with a long run equilibrium with a higher equilibrium interest rate.

I do not think that the "perversity" I am trying to illustrate depends on the distinction between discrete technologies and smooth production functions. I am aware, however, of a theorem that applies to a technology with smooth production functions, but not to discrete technology:

Theorem: Consider an economy in which all produced commodities are basic, in the sense of Sraffa, for all feasible techniques. And suppose the production of one commodity can be described by a continuously differentiable production function. Then this economy cannot exhibit reswitching of techniques.

The relevance of this theorem to my goal is not clear. I am willing to consider examples with non-basic goods. So examples should be possible to construct with smooth production functions and reswitching. But I do not even need reswitching. I am merely looking for capital-reversing. And I do not even insist that real Wicksell effects be positive. I will be content with positive price-Wicksell effects swamping negative real Wicksell effects.

Maybe the kind of example I am seeking is set out in a end-of-the-chapter problem in Heinz D. Kurz and Neri Salvadori's 1997 book, Theory of Production: A Long-Period Analysis (Cambridge University Press).

By looking at the convexity of the wage-rate of profits curves on the frontier, one can read off the direction of price Wicksell effects. And I have already shown that an example can be created with Cobb-Douglas production functions and positive price Wicksell effects. I have yet to examine the relative sizes of price and real Wicksell effects in the example, derive conditions on their directions and sizes, or create a numeric example satisfying those conditions.

Eventually, I would like to explore the dynamics of non-stationary equilibrium paths in such a model built on unarguably neoclassical premises. The point is to continue an internal critique of neoclassical microeconomics, not to describe actually existing capitalist economies.

Choice of Technique, A Two Good Model, Cobb-Douglas Production Functions

Figure 1: Wage-Rate of Profits Curves and their Frontier

1.0 Introduction

This post is a generalization of a neoclassical one-good model. It advances a comparison of Sraffian analysis of the choice of the cost-minimizing choice of the technique and neoclassical analyses, correctly understood, of marginal productivity. Accordingly, all production functions are smooth in this example. If substitutability is seen as a technological property of production functions, then the single capital good and labor can be substituted in each of the two industries in this model.

2.0 The Technology

Consider a simple economy in which steel and corn are produced from inputs of steel and labor. The steel used as an input in production is totally used up in yearly cycles, and the outputs become available at the end of the year. In other words, this is a model without fixed capital, and all production processes require a year to complete.

2.1 Production Functions

The production function for steel is:

Q₁ = F₁(X₁, L₁) = A₁ X₁^α₁ L₁^{(1 - α₁)}

where:

• Q₁ is (gross) output of steel (in tons).
• X₁ is steel (tons) used as a capital good in the steel industry.
• L₁ is labor (person-years) used as an input in the steel industry.

and A₁ and α₁ are positive constants such that:

0 < α₁ < 1

The production function for corn is:

Q₂ = F₂(X₂, L₂) = A₂ X₂^α₂ L₂^{(1 - α₂)}

where:

• Q₂ is (gross) output of corn (in bushels).
• X₂ is steel (tons) used as a capital good in the corn industry.
• L₂ is labor (person-years) used as an input in the corn industry.

and A₂ and α₂ are positive constants such that:

0 < α₂ < 1

2.2 A Set of Coefficients of Production

An alternative specification of this Constant-Returns-to-Scale (CRS) technology is as a set of coefficients of production a₀₁(s₁), a₀₂(s₂), a₁₁(s₁), a₁₂(s₂) from the set:

{ (a₀₁(s₁), a₀₂(s₂), a₁₁(s₁), a₁₂(s₂)) | 0 < s₁, 0 < s₂}

where:

a₀₁(s₁) = [1/(A₁s₁)]^{[1/(1 - α₁)]}

a₀₂(s₂) = [1/(A₂s₂)]^{[1/(1 - α₂)]}

a₁₁(s₁) = s₁^(1/α₁)

a₁₂(s₂) = s₂^(1/α₂)

and

• a₀₁(s₁) is the labor required, in the steel industry, per ton steel produced.
• a₀₂(s₂) is the labor required, in the corn industry, per bushel corn produced produced.
• a₁₁(s₁) is the steel input required, in the steel industry. per ton steel produced (gross).
• a₁₂(s₂) is the steel input required, in the corn industry, per bushel corn produced.

2.0 Quantity and Price Equations, Given the Technique

Consider a stationary state in which the firms employ one person-year of labor each year, and prices are stationary. For notational convenience below, define the following function:

f(R) = (a₀₁a₁₂ - a₀₂a₁₁)R + a₀₂

2.1 Quantity Relations

The amount of steel produced each year, measured in tons, is:

q₁ = a₁₂/f(1)

The amount of corn produced each year, measured in bushels, is:

q₂ = (1 - a₁₁)/f(1)

These quantities must satisfy two equalities. First, the amount of labor employed is unity:

1 = a₀₁q₁ + a₀₂q₂

Second, consider the following equation:

q₁ = a₁₁q₁ + a₁₂q₂

The left-hand side of the above equation denotes the quantity of steel produced each year and available, as output from the steel industry, at the end of each year. The right-hand side denotes the sum of steel used as inputs in the steel and corn industries, respectively. These inputs must be available at the start of each year. Hence, the above equation is a necessary condition when the economy is in a self-sustaining, stationary state.

2.2 Price Relations

I take the consumption good, corn, as the numeraire. The price of steel, in units of bushels per ton, is

p = a₀₁/f(1 + r),

where r is the rate of profits. The wage is:

w = [1 - a₁₁(1 + r)]/f(1 + r)

The above equation is known as the wage-rate of profits curve.

The price of steel, the wage, and the rate of profits must satisfy two equations. The condition that the price of steel just cover the cost of producing steel is:

pa₁₁(1 + r) + a₀₁w = p

The left-hand side of the above equation shows the cost of producing a ton of steel. Costs are inclusive of normal profits, so to speak, on the cost advanced to purchase physical inputs at the start of the year. In this case, those inputs consist of steel, the single capital good in this model. Although labor is hired at the start of the year to work throughout the year, the price equations in this model show labor being paid out of the harvest gathered at the end of the year.

The condition that the price of corn just cover the cost of producing corn yields a similar equation:

pa₁₂(1 + r) + a₀₂w = 1

2.3 The Capital-Labor Ratio

"Capital" is an ambiguous term. It denotes both physically-existing means of production. And it denotes the value of those means of production, when embedded in certain social relations. For example, in this model, the distribution of the capital goods over the two industries is assumed to be appropriate to the continued self-reproduction of the economy. In a sense, the plans of entrepreneurs and firms managers are coordinated.

At any rate, the relationships described so far allow one to express the value of capital, in numeraire units, per person-years, given the technique:

k = p q₁

k = a₀₁a₁₂/[f(1)f(1 + r)]

The capital-labor ratio (in units of bushels per person-years) does not appear in any legitimate marginal product. Nevertheless, I find it a useful quantity for further analysis in multicommodity models.

3.0 The Chosen Technique

The cost-minimizing technique differs with the rate of profits. For analytical convenience, I take the rate of profits as exogenous in this model. One could, instead, if one so chose, take the wage as given and find the rate of profits endogenously. At any rate, this model is open, and the distribution of income is not determined in the model. The equations below set out each of the four coefficients of production in this model as functions of the rate of profits:

a₀₁ = (1/A₁)^{[1/(1 - α₁)]} [(1 + r)/α₁]^{[α₁/(1 - α₁)]}

a₀₂ = (1/A₂)

x {(1 - α₂)/[(α₁)^{[α₁/(1 - α₁)]}(1 - α₁)α₂]}^α₂

x [(1 + r)/A₁]^{[α₂/(1 - α₁)]}

a₁₁ = α₁/(1 + r)

a₁₂ = (1/A₂)

x [(α₁)^{[α₁/(1 - α₁)]}(1 - α₁)α₂/(1 - α₂)]^{(1 - α₂)}

x [A₁/(1 + r)]^{(1 - α₂)/(1 - α₁)}

3.1 Steel as a Basic Commodity and the One-Good Case

I have previously set out an analysis of the choice of technique for a one-good model with an aggregate Cobb-Douglas production function. In the two-good model set out in this post, the coefficients of production for steel, a₀₁ and a₁₁, when the cost-minimizing technique is chosen, are the same as the coefficients of production in that one-good model. This is not surprising.

In the model in this post, steel enters, as an input, into the production of both steel and corn, for all possible techniques. On the other hand, corn never enters as an input into the production of any commodity. In the technical terminology of post-Sraffian economics, steel is always a basic commodity, and corn is never a basic commodity. Thus, the production of steel can be analyzed, in some sense, prior to the analysis of the production of corn.

3.2 A One-Good Special Case

Consider the special case in which:

α₁ = α₂ = α

A₁ = A₂ = A

In effect, steel and corn are the same commodity. The coefficients of production, for the cost-minimizing technique are:

a₀₂ = a₀₁ = (1/A)^{[1/(1 - α)]} [(1 + r)/α]^{[α/(1 - α)]}

a₁₂ = a₁₁ = α/(1 + r)

So this case reduces to the one-good model, as it should. This concludes my analysis of this special case.

4.0 The Chosen Technique on Unit Isoquants and Marginal Productivity Conditions

The coefficients of production are such that the steel industry lies on its unit isoquant:

1 = F₁(a₁₁, a₀₁)

Likewise, the corn industry lies on its unit isoquant:

1 = F₂(a₁₂, a₀₂)

Since the coefficients of production in Section 3 above are for the cost-minimizing technique, all valid marginal productivity relationships must hold. I have chosen to express each marginal productivity condition in numeraire units per unit input. And, the cost of an input and its marginal product are equated here at the end of the year.

Following these conventions, the following display equates the cost of steel to the value of the marginal product of steel in the steel industry:

p(1 + r) = p ∂F₁(a₁₁, a₀₁)/∂a₁₁

Likewise, the following display equates the cost of steel to the value of the marginal product of steel in the corn industry:

p(1 + r) = ∂F₂(a₁₂, a₀₂)/∂a₁₂

Since wages are paid out of the harvest, the rate of profits does not appear in my statement of marginal productivity conditions for labor. The following display equates the wage and the value of the marginal product of labor in the steel industry:

w = p ∂F₁(a₁₁, a₀₁)/∂a₀₁

Likewise, the following display equates the wage and the value of the marginal product of labor in the corn industry:

w = ∂F₂(a₁₂, a₀₂)/∂a₀₂

I have checked the above equations for the isoquants and the four marginal productivity equations. This is quite tedious.

Above, I have listed six equations, two expressing the condition that the coefficients of production lie upon unit isoquants and four marginal productivity equations. These six equations are sufficient to determine the six unknowns (w, p, a₀₁, a₀₂, a₁₁, and a₁₂) in terms of the model parameters and the externally specified rate of profits. In other words, this model illustrates that marginal productivity is a theory of the choice of technique, not of the (functional) distribution of income.

5.0 The Wage-Rate of Profits Frontier

An alternate analysis of the choice of technique can be based on the wage-rate of profits frontier. And this analysis yields the same answer as the above analysis based on marginal productivity.

Recall, from Section 2.2, that a technique can be specified as an ordered pair chosen from the specified index set. The index variables for the cost-minimizing technique, as a function of the rate of profits are:

s₁ = [α₁/(1 + r)]^α₁

s₂ = (1/A₂)^α₂

x [(α₁)^{[α₁/(1 - α₁)]}(1 - α₁)α₂/(1 - α₂)]^{[(1 - α₂)α₂]}

x [A₁/(1 + r)]^{[(1 - α₂)α₂/(1 - α₁)]}

I think it of interest to note that both the optimal process for producing steel and the optimal process for producing corn, in a stationary state, vary continuously with the rate of profits. This is not a generic result for a discrete technology. In a discrete technology, the cost-minimizing techniques at a switch point typically differ in the process used in only one industry; a small variation in the rate of profits thus affects only the specification of a process in one industry.

5.1 First Order Conditions

Since the coefficients of production are functions of the index variables, the wage-rate of profits curve for a technique can be viewed as a function of:

• The index variables s₁ and s₂,
• The rate of profits r, and
• The model parameters α₁, A₁, α₂, and A₂.

A necessary condition for a technique to be cost-minimizing, at a given rate of profits, is that the wage be a maximum. This maximum is taken from the wage on each wage-rate of profits curve, over all techniques. In the current context, with a model with smooth production functions, the first derivative of the wage-rate of profits frontier, with respect to each index variable, must be zero at the maximum:

∂w/∂s₁ = 0

∂w/∂s₂ = 0

Note that the above is a system of two equations in the two unknown index variables. I did not actually calculate the above derivatives for this model. Perhaps Figure 1 provides some confidence in this mathematics. I deliberate drew three wage-rates of profits curves on the frontier and one off of it.

5.2 Second Order Conditions

The FOCs determine a critical point. The calculus is consistent with such a critical point being a local maximum, a local minimum, or a saddle point. The following are sufficient conditions, in this context, for a critical point to be a local maximum:

∂²w/∂s₁² < 0

∂²w/∂s₂² < 0

D(s₁, s₁) > 0

where D(s₁, s₁) is defined by:

D(s₁, s₁) = [∂²w/∂s₁²][∂²w/∂s₂²] - [∂²w/∂s₁∂s₂]²

Of the three SOCs, either the first or the second is redundant.

6.0 Conclusion

I still have some ideas for future work with this model. But I think this is enough for one blog post. I hope the above presentation suggests that marginal productivity is not a theory of distribution, in general. One cannot validly hold, for example, that real wages are determined by the marginal product of labor. Furthermore, the Sraffian analysis of the choice of technique is analytically equivalent to the determination of the choice of technique, given, for example, the rate of profits, by marginal productivity.

Choice Of Technique With A Smooth Aggregate Production Function

Figure 1: Coefficients of Production for the Technology

1.0 Introduction

This post advances, somewhat, my start at a reconsideration of the dynamics of Overlapping Generations Models (OLGs). Only the production side of a stationary state is considered here. Furthermore, only a very special case - namely, a one-good model - is analyzed here.

I guess the most exciting aspect of this post is an illustration of the claim that the construction of the wage-rate of frontier is useful for the analysis of the choice of technique for "smooth" production functions, not just for discrete technologies. I have never understood, for at least a quarter of a century, why some economists seem to talk as if a fundamental distinction exists between such models. In some contexts, some conclusions differ. But it seems to me to be silly to say that the Cambridge Capital Controversy turns around an empirical question on the degree of substitutability of inputs in production.

2.0 Specification of Technology

Consider a simple economy in which corn is produced from inputs of labor and corn. Assume the existence of Constant Returns to Scale (CRS). A technique is specified by an ordered pair of coefficients of production, where each ordered pair is from a set containing a continuum of such ordered pairs:

{ [a₀(s), a₁(s)] | 0 < s < 1}

where:

a₀(s) = 1/(A s)^{1/(1 - α)}

a₁(s) = s^1/α

and α and A are specified positive parameters such that:

0 < α < 1

Figure 1 graphs the coefficients of production as a function of the index s. All graphs are draw for a value of α of 1/4 and of A of 5.

3.0 Derivation of the Cobb-Douglas Production Function

The above specification of the technology shows, for a unit output of corn, a smooth trade-off of inputs of labor and corn inputs. This specification of technology allows for the derivation of a conventional production function. The following is an equation for a unit isoquant for this technology:

1 = A [a₁(s)]^α [a₀(s)]^{1 - α}

Define:

• Q is (gross) corn (bushels) output.
• L is labor (person-years) input.
• X is (seed) corn input.

From CRS, it follows:

Q = A [Q a₁(s)]^α [Q a₀(s)]^{1 - α}

Or:

Q = A X^α L^{1 - α}

The last equation above is how the (in)famous Cobb-Douglas production function is typically represented. So the specification of technology used in this post is a (non-unique) representation of a Cobb-Douglas production function.

4.0 Analysis of the Choice of Technique

For a given technique, Sraffa's price equations become one equation:

a₁(s)(1 + r) + a₀(s) w = 1

where:

• r is the rate of profits
• w is the yearly wage (in units of bushels per person-year).

The price equation embeds the assumptions that production of corn requires a year to complete and that labor is paid out of the yearly harvest. One can derive a wage-rate of profits curve from the price equations:

w(r, s) = [1 - a₁(s)(1 + r)]/a₀(s)

In this case, each wage-rate of profits curve is a straight line. Figure 2 shows three selected wage-rate of profits curves.

Figure 2: Wage-Rate of Profits Curves and Their Frontier

Figure 2 shows, in violet, the outer wage-rate of profits frontier. When firms choose the cost-minimizing technique in a steady state, the economy will lie on this curve. (In this case, with a continuum of techniques, each point on the frontier is a non-switch point.) A closed-form expression for the wage-rate of profits frontier is easily derived. The First Order Condition (FOC) for the choice of technique can be expressed as equating the derivative, with respect to the index variable, of the wage-rate of profits curve to zero:

dw/ds = 0

The FOC yields an equation which can be solved for the index variable:

s(r) = [α/(1 + r)]^α

So the coefficients of production, for the cost-minimizing technique, can be found as functions (Figure 3) of the rate of profits:

a₀(r) = [1/A^{1/(1 - α)}] [(1 + r)/α]^{α/(1 - α)}

a₁(r) = α/(1 + r)

Thus, the desired expression for the wage-rate of profits frontier is:

w(r) = (1 - α) A^{1/(1 - α)} [α/(1 + r)]^{α/(1 - α)}

In this special case, the desired amount of labor per unit output is higher, the lower the wage. Likewise, the desired amount of the capital good per unit output is lower, the higher the rate of profits. These results do not generalize to multi-commodity models.

Figure 3: Optimal Coefficients of Production

5.0 Capital Intensity

In this special case, the ratio of the value of capital goods to labor can be calculated in physical terms, without addressing a question of valuation. That is, the capital-labor ratio, as a function of the rate of profits (Figure 4), is easily derived:

I(r) = a₁(s(r))/a₀(s(r)) = [α A/(1 + r)]^{1/(1 - α)}

In this special case, the capital-labor ratio is a downward-sloping, single-vauled function of the rate of profits. These properties do not generalize, either.

Figure 4: Capital Intensity